加工路线最优方案设计研究
彭三河
(长江大学机械工程学院,湖北 荆州 434023)
加工路线最优方案设计研究
彭三河
(长江大学机械工程学院,湖北 荆州 434023)
通过建立加工路线网络图,根据动态规划的最优化原理,对加工时间、加工费用进行计算,确定了最优的加工路线。
网络图;加工时间;加工费用;加工路线
在某个确定的目标(如加工时间最短、加工费用最小)和在某些约束条件(如制造厂的实际情况、年产量、合同交货期以及投资额等)下,在诸多可行的加工路线方案中选择最合理的方案,这就是加工路线设计的最优化问题。
按照系统工程的观点,加工路线最优化是一个多阶段决策问题。根据各个阶段局部的比较,并不能得到最优化决策顺序,要圆满地解决这个问题,需要按照加工路线建立网络图,然后根据动态规划的最优化原理进行计算[1,2]。
1 建立加工路线网络图


图1 网络单元示意图Figure 1 Schematic diagram of network unit
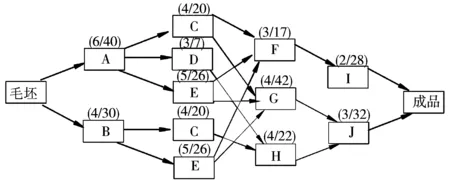
图2 加工路线流程框架图Figure 2 Processing of the road map process framework
在画网络图时,两结点之间的工序必须是唯一的,不允许存在两个或两个以上的工序。如果出现这种情况,可以引入虚工序(图1),以便于计算机处理。虚工序是不耗时间、人力和物力的。
举例来说,设有一个由4个阶段组成的加工路线,根据零件的加工要求以及现有设备状况,每一阶段均可由一些不同的工序完成,其流程框架图如图2所示。图2中每个方框代表一种可行的工序,方框旁括号的数字,分子表示该工序的加工时间(h),分母表示加工费用(元)。根据加工路线的框图即可建立网络图,如图3所示。
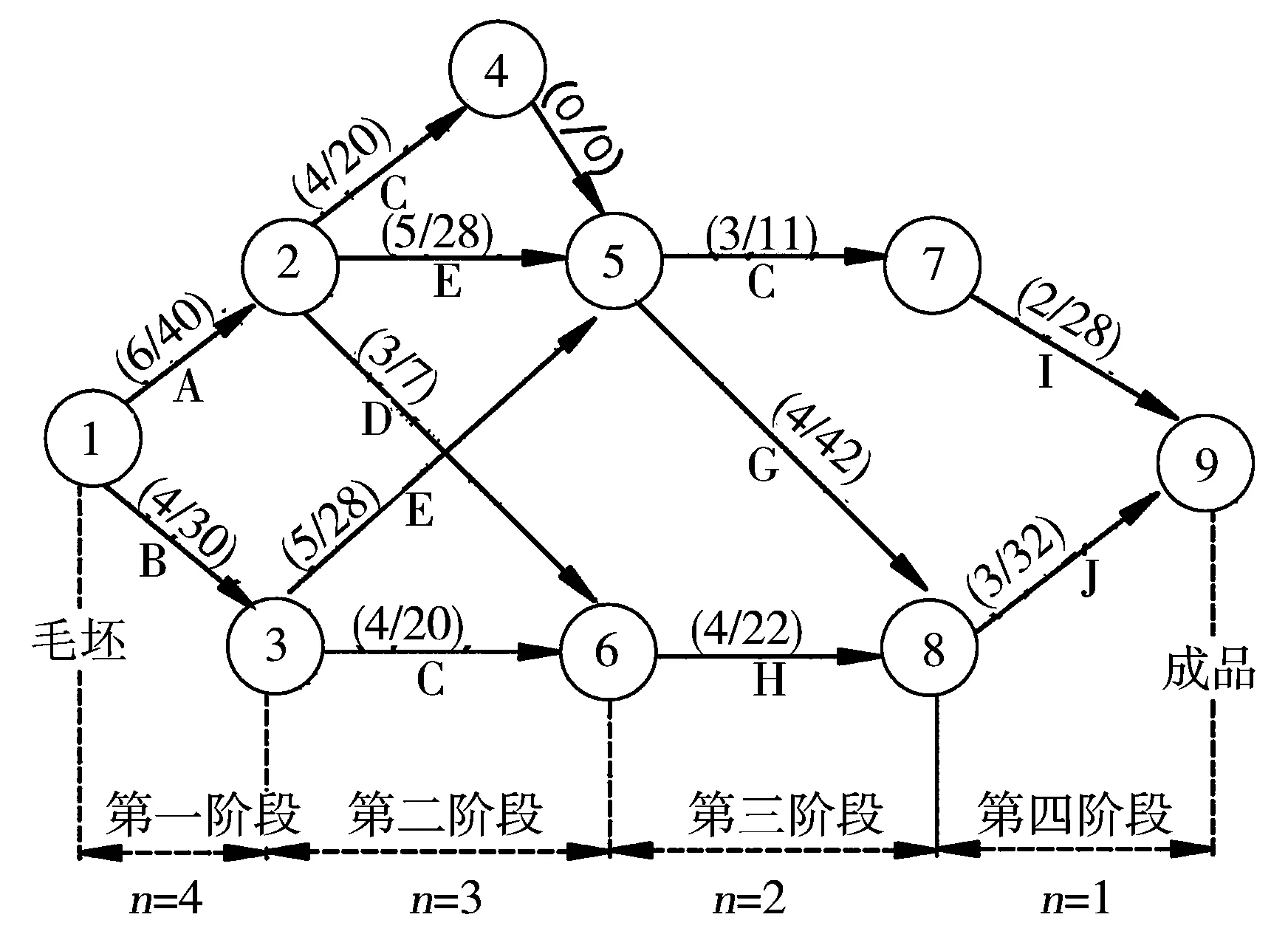
图3 加工路线网络图Figure 3 Processing of the road network map
2 加工路线优化
关于这种具有有限组合(本例共8种)的最优化问题,如果对于所有可能的组合均计算总的加工时间(或者加工费用),然后从中选取最小者作为最优方案,这当然可以。 不过, 如果路线较多,计算量会过大,而且缺乏实用价值,这时应根据动态规划的最优性原理来解。一个最优策略应具有这样的性质,不管初始状态和初始决策是什么,对于先前的决策所形成的状态而言,其后的所有决策必须构成最优策略。
2.1 加工时间优化
为了求解上述例题中加工时间最短加工路线,根据最优性原理写出下列关系式[3,4]:
tn(i)=min[tij+tn-1(j)]
j
式中,tn(i)为性能指标的最小值,既由现在的结点i到终点9所需的最短时间;tij为工序(i,j)的加工时间;tn-1(j)为从下一结点j到终点9所需的最短时间。
显然,t0(9)=0。
从后往前求解,第4阶段:
t1(8)=min[t8j+t0(j)]=t89+t0(9)=3 (8→9)
j=9
t1(7)=min[t7j+t0(j)]=t79+t0(9)=2 (7→9)*
j=9
这里,最右端括号内的不同(i→j)分别表示本阶段的决策,而有*者才属于整个系统的最优决策序列。
第3阶段:
t2(6)=min[t6j+t1(j)]=4+3=7 (6→8)
j=8
t2(5)=min[t5j+t1(j)]=min[3+2,4+3]=5 (5→7)
j=7,8
t2(4)=t2(5)=5 (4→5→7)
第2阶段:
t3(3)=min[t3j+t2(j)]=10 (3→5)*
j=5,6
t3(2)=min[t2j+t2(j)]=9 (2→4)
j=4,5,6
最后,第1阶段:
t4(1)=min[t1j+t3(j)]=14(1→3)*
j=2,3
根据上述分析结果,总加工时间最短的路线为:1→3→5→7→9,一共需要14 h。相应的加工路线为:工序B→工序E→工序F→工序I。
2.2 加工费用优化
为了求解加工费用最小的加工路线,根据最优性原理可以写类似的关系式:
Cn(i)=min[Cij+Cn-1(j)]
式中,Cn(i)为性能指标的最小值,由现在的结点i到终点9所需要的最少费用;Cij为工序(i,j)的加工费用;Cn-1(j)为从下一结点j到终点9所需的最少费用;显然C0(9)=0。
同样从后往前求解,得到总加工费用最少的路线为:1→2→6→8→9,一共需要101元。相应的加工路线为:工序A→工序D→工序H→工序J。
2.3 其它方面优化
上述分析为采用现有设备的情况,如果所拟订的加工路线方案中需要新购置自动化高效设备,设计和制造专用设备,或者采用新工艺,则应按照下列方法进行经济评比。
(1)现在价值分析法 新投资方案的现在价值为:
式中,S为新投资方案的现在价值(元);Sj为新设备第j年度的现金收入(元);N为新设备的寿命周期(年);r为年利率。
这里, 1/(1+r)j称为现值系数,它是用来将j年度现金收入折算成投资那一年的数值,当现在价值的累计总额大于设备投资时,认为投资方案是合理的。
(2)投资收益法 新投资方案的收益为:

式中,P为设备方案的收益率;Sj为第二年估计从该设备可获利的金额(元);I为新设备的购置费(元);V为新设备使用第一年的折旧费(元);R为原有设备现在卖出可得的金额(元)。
当投资收益率比较大时,认为可以采用新设备或新加工替代原有的。
3 小结
由上述实例可知,在现有设备的情况下加工一个零件,对于所有可能的组合均计算总的加工时间或加工费用,其中最小者就是加工路线的最优方案。
[1]Lee H F,Stecke K E. An integrated design support system for flexible assembly systems[J].Journal of Manufacturing Systems,1996,15:13~32.
[2]Philippe S,Mario V V. Analytical models for FMS design optimization: a survey[J].International Journal of Flexible Manufacturing Systems,1994,6:209~233.
[3]李建勇, 鄂明成,查建中. 基于混合遗传算法的工艺路线优化配置[J]. 机械科学与技术, 2003,(6):21~23.
[4]钱显志,郑联语,魏 丽. 多工艺路线可视化设计与评估方法[J]. 北京航空航天大学学报, 2005,(7):41~44.
2009-09-25
湖北省教育厅资助项目(D200512003)
彭三河(1963-),男 湖北红安人,副教授,主要从事农业机械设计研究.
10.3969/j.issn.1673-1409(S).2009.04.021
TH162
A
1673-1409(2009)04-S071-03

