哪种解法更贴近实际生活

吴　智

题目:一块长方形麦田的长是500米,宽是300米。如果射程是10米的自动旋转喷灌装置进行喷灌,大约需要多少个这样的喷灌装置?

在教学中,数学组老师对此题的解答至今没有一个统一说法,存在较大的差异。

第一种解法:用长方形的面积除以每个喷灌的喷射面积,得出需要多少个喷灌装置,即500×300÷(3.14×10×10)≈478(个)或477个(其中采用进一法取近似值为478个,采用去尾法取近似值为477个)。理由是因为喷灌喷出的图形呈圆形,因此,求出麦田面积包含有多少个圆形的面积,即可得出需安装几个喷灌装置。这种解法采用了包含除法的思路思考,从数学角度来说这种解法是合理的。然而,我们仔细想想,不难发现,这种思路存在明显的错误。大家知道在正方形或长方形里剪圆形,定会剩下边角料,边角料怎么又能拼成一个圆形呢?更何况这是块麦田呢?边角料更不能拼在一起。可见,这是一种理论上答案。

第二种解法:用长方形面积除以对角线为20米长的正方形面积,即500×300÷(10×10×2)=750(个)。理由是:由于每个喷灌装置能喷灌的面积都是以10米为半径的圆形,而麦田是长方形的,要想使喷灌的面积覆盖整块麦田,必须有重喷的面积,并且在实际应用中,这些喷灌喷射的面积是很难做到不重复、不遗漏的。因此,可用在圆内剪最大的正方形面积的方法来计算所用喷灌装置的个数(如下图)。笔者认为,这也是一种理论上的解法,它完全脱离了生活实际。大家试想一下,假如按照这样的设计来安装喷灌装置,花费的人力、物力、财力比第一种方法多得多,谁愿意这样做呢?此外,这种方法虽然能使喷灌的面积完全覆盖,但对水资源的浪费极其严重,因为它重复喷灌的面积比较多。

可见,以上两种解法都是理想形的解法。笔者认为,此题采用如下的方法解答较为贴近实际生活。题中射程是10米即喷灌喷出图形是半径为10米圆形,那么在半径为10米的圆外切一个正方形,即在正方形内剪一个最大的圆,正方形的边长约10×2=20(米)。如下图:

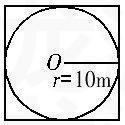
由此可以这样想:用长方形麦田的面积除以正方形的面积,可得出需要多少个喷灌,即500×300÷(20×20)=375(个)。也许有人会问:“这样解法,喷灌装置的面积覆盖不了整块麦田啊?”其实,在实际生活中,人们安装喷灌装置真的要把整块麦田的一点一滴都喷灌吗?不以为然吧。其实,水是一种液体,可以自由流动,并慢慢地渗透到邻近的土块里,没有必要覆盖整块麦田。同时,这种设置比前两种省时、省力、省财,何乐而不为?