简单选择排序算法的改进及分析

张忆文　谭　霁

[摘要]排序是计算机程序设计的重要操作,经典的排序包括:冒泡排序、选择排序、插入排序等等;以简单选择排序算法为基础,对其进行改进,通过分析得出与之具有同样行之有效、甚至更高的排序效率。

[关键词]简单选择排序 改进算法 分析

中图分类号:TP3文献标识码:A文章编号:1671-7597(2009)0920077-01

排序是将数据元素的任一序列,重新排列成一个关键字有序的序列。基于比较和移动的排序算法具有通用性,包括插入排序、选择排序、交换排序、归并排序、计数排序[1]。各种排序的算法各具有优缺点,但就其全面性能而言,很难提出一种被公认的最好的方法。评价算法主要考虑其时间复杂度、空间复杂度、稳定性等。笔者通过对简单选择排序算法进行改进,使其交换或移动的次数减少,从而提高效率。

一、简单选择排序[2]

简单选择排序的基本思想:对待排序的序列进行若干趟处理,通过n-i次关键字的比较,从n-i+1个记录中选出关键字最小的记录和第i(1≤i≤n)个记录进行交换,这样一趟处理就能确定一个数的位置,对n个数如果确定n-1个数的位置,则这n个数就排序成功。

(一)主要代码片段

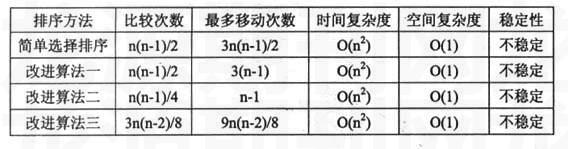
for(i=0;i

{for(j=i+1;j

if(a[i]>a[j])

{t=a[i];a[i]=a[j];a[j]=t;}}

(二)算法分析

时间复杂度:简单选择排序过程中,当待排序序列为正序时,移动的次数最少为0次;当为逆序时最大为3n(n-1)/2;然而无论记录是否有序所需比较的次数都为n(n-1)/2;所以时间复杂度为O(n2)。

二、改进算法一

简单选择排序在每趟中都选一个最小的关键字确定其正确的位置,上述算法只要相邻元素逆序就要交换(移动);可以附设一个变量记录其最小值,然后在与最小值交换,这样可以大大的减少移动的次数。

(一)主要代码片段

for(i=0;i

{k=i;

for(j=i+1;j

if(a[i]>a[j])

k=j;

if(k!=i)

{t=a[i];a[i]=a[j];a[j]=t;}}

(二)算法分析

时间复杂度:当待排序序列为正序时,移动的次数最少为0次;当为逆序时最大为3(n-1),这比3n(n-1)/2大大的减少;比较的次数为n(n-1)/2;所以时间复杂度为O(n2)。

三、改进算法二

简单的选择排序在一趟排序的过程只能确定一个元素的正确位置,现改进为在一趟的排序过程中确定两个元素的位置,即一个最大值和一个最小值。对一个待排序序列应比较第一个元素和最后一个元素的值,若逆序就交换,这样可以保证第一个元素比最后一个元素小;将2到n-1个元素依次同第一个元素比较;若逆序则交换;否则和最后一个元素比较若逆序则交换;这样在一趟排序过程中就确定两个元素的位置;对剩余的n-2个元素,重复上述过程直至全部有序[3]。

(一)主要代码片段

for(i=1;i<=n/2;i++)

{if(a[i-1]>a[n-i])

{t=a[i-1];a[i-1]=a[n-i];a[n-i]=t;}

for(j=i;j

if(a[i-1]>a[j])

{ t=a[i-1];a[i-1]=a[j];a[j]=t;}

else if(a[j]>a[n-i])

{t=a[j];a[j]=a[n-i];a[n-i]=t;}}

(二)算法分析

时间复杂度:当待排序序列为正序时,移动的次数最少为0次;最坏时所需的移动次数为n-1,大大的低于简单选择排序的3n(n-1)/2;从比较次数来看,循环的次数减少一半,所以比较的次数为n(n-1)/4相对与简单选择排序也有所降低。 所以时间复杂度为O(n2)。

四、改进算法三

利用分治法的思想将第一个数和最后一个数比较若逆序,则交换;第二个数和倒数第二个数比较若逆序,则交换;直至第i个数和第i个数比较;将待排序序列分成两部分,将小者放在前半部分,大的放在后半部分,然后再在前半部分选出最小值;后半部分选出最大值;对剩余的n-2个数做同样的处理,直至全部有序。

(一)主要代码片段

for(i=0,j=n-1;i<=j;i++,j--)

{while(i

if(a[i]>a[j])

{t=a[i];a[i-]=a[j];a[j]=t;i++;j--}

k=i-1;static m=0;static l=n-1;

for(t=m;t

if(a[t]>a[t+1])

{ r=a[t];a[t]=a[t+1];a[t+1]=r;}

for(t=k;t

if(a[t]>a[t+1])

{r=a[t];a[t]=a[t+1];a[t+1]=r;}

m++;l--;}

(二)算法分析

第一趟在n个元素的序列比较n/2(n为偶数)次或为(n+1)/2次(n为奇数);为讨论方便取n为偶数;在前半部分选出最小值要比较n/2-1次;后半部分选出最大值需要比较n/2-1次;所以在一趟排序确定两个元素的正确位置要3n/2-2次。在剩余的n-2个元素中确定两个元素的正确位置需要3(n-2)/2-2次;以此类推可知最后一趟剩余的两个元素的比较次数为1次;所以总的比较次数为3n(n-2)/8;这比简单选择排序也有所降低。当待排序序列为正序时,移动的次数最少为0次;最坏时所需的移动次数为9n(n-2)/8比简单选择排序也有所降低。

五、各种排序的比较

六、结束语

各种改进方法的思想和简单的选择排序基本一致;都是在简单选择排序的基础上加以改进;使之成为一种更简单,效率更高的算法。

参考文献:

[1]严蔚敏等,数据结构(C语言版)[M].北京:清华大学出版社,2005.7.

[2]潭浩强,C程序设计[M].北京:清华清华大学出版社,1999.4.

[3]何洪英,双向选择排序算法的实现及性能研究,成功(教育),2007.9.

作者简介:

张忆文,男,本科生,长江师范学院数学与应用数学专业;谭霁,男,本科生,长江师范学院数学与应用数学专业。