税收征纳中的博弈分析
兰 敏 刘造林
[摘 要] 本文旨在运用博弈论的有关知识,通过建立税收征纳模型来分析现实生活中征税方与纳税方的关系及其存在的问题,并从双方的博弈关系中得出几点建议与思考。
[关键词] 税收征纳;混合策略;纳什均衡
[中图分类号]F810.423;F224.32[文献标识码]A[文章编号]1673-0194(2009)01-0046-03
税收收入是我国财政收入的重要组成部分,一般来说,税收收入都会占到财政收入的90%以上,可见,保证税收收入的及时缴纳,防止偷税逃税等对一个国家是极其重要的。但是,对于纳税人来讲,税收是他们的一项费用支出,国家征收税款,虽然说是“取之于民,用之于民”,但很多纳税人并不愿意主动缴纳税款,总希望能够逃避这项义务,正是由于国家和纳税人之间在征纳关系方面存在矛盾,因此,国家一方面大力宣传依法纳税知识,另一方面又不断完善税收征管法,期望使纳税人主动纳税,同时使税务机关减轻征管负担。那么在实际生活中,征纳方之间的矛盾能否有效地解决呢?本文就此问题,通过建立博弈模型来分析税收征纳关系,以期构建一个完善的税收征纳体系。
一、税收征纳关系中的行为主体分析
经济学对人的行为的考察是建立在“理性人”的理论假设基础上的,研究税收征纳关系中的各类主体同样也要以这个假设为基础。在现实生活中,征纳双方都是追求自身利益最大化的,因而他们在作出一定行为之前总要对各种可选行为方式的成本和收益大小进行分析比较,从中选择能给自己带来最大利益的行为。
从理论上讲,征税主体是国家,而在实际执行过程中,国家却将征税的权力委托给了税收征管人员,因此,博弈行为会出现在征税人与国家、征税人与纳税人、征税人与征税人以及纳税人与纳税人等各类行为人之间。
这些错综复杂的博弈行为给税收征管带来了相当大的困难,在各方追求利益最大化的前提下,征税人有可能因为私利而损害国家利益,而纳税人之间也可能存在逃避税款与告发之间的博弈。当然,在这诸多博弈中,最重要的还是征税人与纳税人之间的博弈。一方面,纳税人总存在偷税的意图,另一方面,征税人又会通过稽查等手段防止偷税事件的发生。因此,本文就用博弈论的知识来加以阐释征税方与纳税方之间为追求各自利益最大化而作出的行为。
二、税收征纳关系中完全信息条件下的静态博弈分析
(一)博弈的概念与要素
博弈论是描述和研究行为者之间策略相互依存和相互作用的一种决策理论,任何一种博弈都必须具备3个基本要素:参与者、策略和得益。在每一个博弈中,都至少有两个参与者,每一个参与者都有一组可选择的策略,作为博弈的结局,每一个参与者都得到各自的得益,其得益可为正,也可为负,每一个参与者所得到的得益都是所有参与者各自所选择的策略的共同作用的结果。
(二)税收征纳模型的假设
首先,作出如下假设:
(1)此博弈为完全信息条件下的静态博弈。
(2)纳税人根据自己的经营情况进行纳税申报,税务人员根据其申报的税额进行征收,并适当进行税务检查,防止纳税人偷逃税款。
(3)纳税人是理性人,为追求自身的利益最大化,他们会在偷税与不偷税之间进行选择。
(4)征税人同样是理性人,为了保证税额足额上缴国库,会在检查和不检查之间进行选择。
(5)为简化分析,假定纳税人偷税即为税款全部未缴,不存在偷逃部分税款的情况。
(6)在博弈分析中,假设征税方的征税成本为A,征税方查出偷逃税款,对纳税人的处罚为B,纳税人应该缴纳的税款为C。
(三)税收征纳模型的建立与分析
(1)当征税方选择检查,纳税方选择偷税时,征税方可以得到处罚和税款,但要减去相应的征税成本,故得益为C+B-A,纳税方则不仅失去税款,同时还须缴纳罚款,因此其得益为-C-B。
(2)当征税方选择不检查,纳税方选择偷税时,征税方将损失处罚和税款收入,因此得益为-C-B,纳税方则可以逃避税款,故其得益为C。
(3)当征税方选择检查,纳税方选择不偷税时,征税方可以得到税款,但要减去相应的征税成本,故得益为C-A,纳税方则缴纳了税款,因此其得益为-C。
(4)当征税方选择不检查,纳税方选择不偷税时,征税方可以得到税款,故得益为C,纳税方则失去税款,因此其得益为-C。
根据以上的假设与分析,可以建立如图1所示的得益矩阵模型来进一步地分析。

图1中的得益矩阵表示征税方有两个策略:检查或不检查,纳税方也有两个策略:偷税或不偷税。
(1)对于纳税方来讲,当他选择偷税时,征税方选择检查还是不检查取决于C+B-A与-C-B的大小,若C+B-A>
-C-B,则征税方选择检查,反之,则征税方选择不检查。但是,要使C+B-A<-C-B,除非使得C+B<A/2,但是由于要使税款和罚款的总和不仅要小于A,而且要小于A/2,除非征税成本是巨额的,这种可能性很小,因此,可认为C+B-A>
-C-B,征税方选择检查,即(偷税,检查)的策略组合。
(2)对于纳税方来讲,当他选择不偷税时,由于C-A <C,所以征税方选择不检查才能达到收益最大化,即(不偷税,不检查)的策略组合。
(3)对于征税方来讲,当他选择检查时,由于-C-B<-C,所以纳税方会选择不偷税,即(检查,不偷税)的策略组合。
(4)对于征税方来讲,当他选择不检查时,由于C > -C,所以纳税方会选择偷税,即(不检查,偷税)的策略组合。
从以上的分析中可以看出,在此博弈中,没有一个策略组合能构成纳什均衡,即不存在纯策略下的纳什均衡。
作为理性的博弈参与者,征税方和纳税方为了不让对方猜透自己的策略而遭受损失,都不会采取纯策略,征纳双方只能按照一定的概率随机选择自己的策略,以确保对方难以猜透自己的行为,即该博弈存在一个混合策略纳什均衡。
(四)税收征纳关系中的混合策略纳什均衡分析
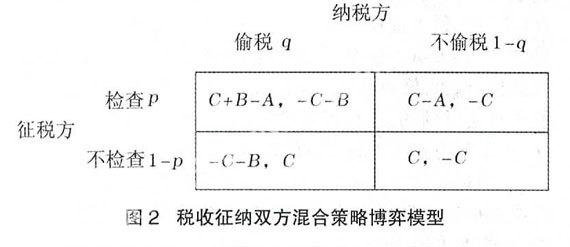
假定征税方检查的概率为p,不检查的概率为1-p;纳税方偷税的概率为q,不偷税的概率为1-q。则税收征纳双方博弈模型如图2所示。
(1)征税方选择检查的期望效用可表示为:(C+B-A)× q+(C-A)×(1-q)=(C-A)+Bq;
征税方选择不检查的期望效用可表示为:(-C-B)× q+ C×(1-q)= -2Cq-Bq+C。
令(C-A)+Bq=-2Cq-Bq+C,
则q = A/(2B+2C)。
(2)纳税方选择偷税的期望效用可表示为:(-C-B)×p+ C×(1- p)= -2Cp-Bp+C;
纳税方选择不偷税的期望效用可表示为:-C×p+[ -C×(1-p)]= -C。
令-2Cp-Bp+C= -C,
则p=2C/(2C+B)。
因此,混合策略组合{[p,(1-p)],[q,(1-q)]},其中p= 2C/(2C+B),q = A/(2B+2C)为该博弈的混合策略纳什均衡。
(3)从以上的分析中可以看出:①纳税方偷税概率与征税成本和税款、罚款的关系密切。当征税方的征税成本增大时,征税方不会十分频繁地进行税收检查,此时纳税人偷逃税款的概率就不可避免地增大了。而当税款与罚款增大时,纳税方偷税概率反而会变小,因为纳税人要顾及到一旦偷税事件被查出,那么根据我国现有的征管法的规定,他会被处以税款的50%以上,5倍以下的罚款,偷税税款越大,罚款也越重。②对于征税方来说,税款越大,则检查概率也越大,因为税收收入是国家收入中极其重要的一部分,征税方为避免税款尤其是巨额税款的流失,势必会增大对这些缴纳巨额税款的企业的检查力度。而当罚款增大时,检查概率会变小,这主要是因为,一旦罚款加重,那么纳税人会心存顾忌,偷税概率会减小,征税方也就没有必要进行大规模检查了。
三、基于模型所得出的几点建议
(1)在现实生活中,税收征纳博弈并不是简单的静态博弈,而是不断的重复博弈过程,征税方要想遏制住纳税方的偷税念头,应该从一开始就从严管理,但又要把握好尺度,防止造成不必要的冲突,反而影响管理。
(2)征税方可以适当提高罚款比例,这种方法通过以上对模型的分析来看,也是切实有效的,可以使纳税人产生惧怕心理,从而减少偷税事件发生的可能性。
(3)征税机关一方面可以改进稽查技术,使得效率更高,花费更少,一方面应加大普法力度,使纳税人自觉进行纳税申报。
(4)在税收征纳关系中,纳税人客观上处于弱势地位,因此有必要通过法律规范来提高纳税人的法律地位,确保纳税人的权利。保障纳税人在税收制度制定中的参与权,可以说是将税收博弈环节前移,使纳税人可以通过立法环节的博弈来降低税负,从而降低在征纳博弈中选择偷税的概率。
四、结 语
税收中的博弈问题纷繁复杂,本文所分析的税收征纳博弈只是众多博弈中的一种,除此之外,还有征税人与征税人之间的博弈,纳税人与纳税人之间的博弈等,因此,在实际运用中,还应该考虑到其他税收关系对征纳的影响,而不能只局限于征纳双方的关系。
主要参考文献
[1] 王则柯,李杰. 博弈论教程[M]. 北京:中国人民大学出版社,2004.
[2] 张维迎. 博弈论与信息经济学[M]. 上海:上海人民出版社,1997.
[3] 邓永勤. 税收征纳模式的博弈分析[J]. 涉外税务,2003(5).
[4] 邓力平,安然. 纳税人遵从的演化博弈分析[J]. 涉外税务,2006(5).

