运用数学知识学历史

闫淑云

教学是一门科学，更是一门艺术，适当引入数学知识，既能使我们的历史课堂内容丰富多彩，又增添了学生的学习兴趣，使学生的知识达到融会贯通。

一、运用曲线图进行直观教学

例一：复习中国古代人口变化情况，如下图。

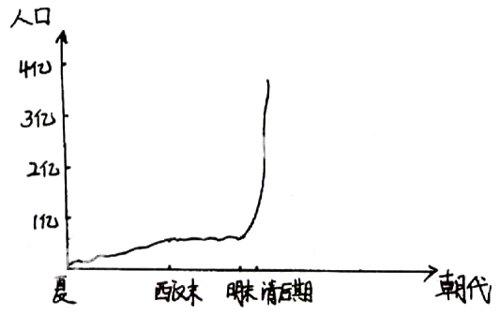
有些历史知识如人口变化、经济发展情况等，分布在课本的各个章节，学生掌握起来比较困难。运用曲线图教学，这些问题便会迎刃而解。

上课时先用多媒体投影出以下资料：纵观数千年来中国人口的发展，我们不难发现，人口总量的增长是中国人口发展中最明显的特征。

1.第一个坡，从夏朝至西汉末年（公元前21世纪到公元初），2000多年时间，中国人口增长沿着一条缓升的总量线波动，直至接近6000万。

2.第二个坡，从东汉至明末（公元初到17世纪初）1600年左右的时间，中国人口增长围绕着一条水平的总量线（6000万至7000万）上下波动。对于宋时期和明时期的人口总量，有学者认为已经达到或突破了1亿。

3.第三个坡，从明末至清后期（17世纪初到1850年），大约200年时间，中国人口增长沿着一条向上倾斜的总量线波动，历经1亿、2亿、3亿，最终达到四亿三千万左右。

教师可以请两名学生在黑板上绘出以上描述的大致曲线图，锻炼学生的绘图能力。由学生自己发现问题，解决问题。教师要适时地提示、点评、总结。

①影响中国古代人口变化的因素有哪些？

②唐朝时人口增多，出现了人地矛盾，当时是如何解决的？带来哪些影响？

③清朝人口猛增的原因主要是什么？

④上述情况对于我们今天制定人口政策有何指导意义？

例二：复习1840~1956年我国主要经济成分。参考下图。

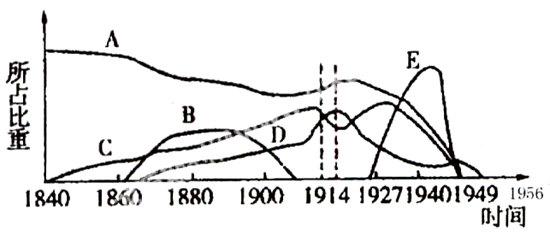
五种经济成分：自然经济、民族资本、外国资本、洋务资本与官僚资本。

教学方法同上例一。

画曲线图是历史分析的一种方法。运用曲线图教学直观、一目了然，教师避免了枯燥乏味的填鸭式教学。我们在探究历史问题的同时与数学知识实现了链接，学生想象力丰富，易于迸发出创造灵感，培养了学生发现问题、解决问题的能力，也令历史课堂充满生机和活力。

二、运用数学换算历史年代，培养学生应用能力

近两年高考常涉及干支纪年问题。怎样将一些历史纪年转化为学生所熟识的公元纪年呢？这就需要数学知识了。

1.干支纪年。

公式：第一步：(公元年份-3)÷60得余数x；

第二步：x÷10所得余数对应天干；

第三步：x÷12的所得余数对应地支。

例如：公元2009年的干支纪年这样计算：

（2009-3）÷60得余数x为26；

26÷10余数为6对应天干“已”；

26÷12余数为2对应地支为“丑”。

故2009年为已丑年。

2.公元换算成年号时，年号年数由“公元年数-年号元年+1”而得。如：641年文成公主入藏是贞观几年？

由“公元年数641-贞观元年627+1”可得641年为贞观15年。

年号换算成公元时，公元年数由“年号年数+年号元年-1”而得。如：民国24年是公元何年？由“民国年数24+民国元年1912-1”可得民国24年为公元1935年。

运用数学换算，学生把前人的认识转化为自己的认识，进而又转化为能力。

三、运用集合方法进行历史教学

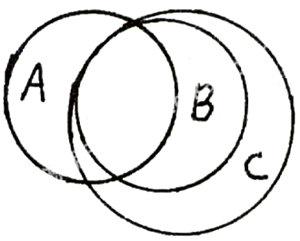
例一：复习近代史上的不平等条约《南京条约》及其附件(即A）、《望厦条约》(即B）和《黄埔条约》（即C）。这些条约单靠死记硬背不仅显得枯燥乏味而且浪费时间。如何能让学生轻松把条约内容记住、记牢是历届师生研讨的重要课题。不妨运用集合方法试试。

先请两名学生在黑板上绘出相应的集合图，然后师生再共同探讨、解决以下问题。

1.找出集合的交集部分：《南京条约》及其附件中除割地、赔款外的一切特权。

2.美国将门户开放得更宽阔，体现在哪里？

3.法国又扩大了哪些侵略权益？

4.通过上述学习，你有何认识？

例二：复习史学著作《史记》(即A）、《汉书》(即B）、《资治通鉴》(即C）。方法同上。

在特定的教学情境中，集合方法能使学生精力集中，观察细致，思维敏捷，识记速度加快，也大大减轻教师的负担，获取了更好的教学效果。总之，恰当运用数学知识，不仅有利于历史的学习，同时在学习历史的过程中，又能更好地理解和掌握数学知识。