Iterative Learning Model Predictive Control for a Class ofContinuous/Batch Processes*

ZHOU Mengfei (周猛飞), WANG Shuqing (王树青), JIN Xiaoming (金晓明) and ZHANG Quanling (张泉灵)



Iterative Learning Model Predictive Control for a Class ofContinuous/Batch Processes*

ZHOU Mengfei (周猛飞), WANG Shuqing (王树青)**, JIN Xiaoming (金晓明) and ZHANG Quanling (张泉灵)

State Key Laboratory of Industrial Control Technology, Institute of Cyber-Systems and Control, Zhejiang University, Hangzhou 310027, China

An iterative learning model predictive control (ILMPC) technique is applied to a class of continuous/batch processes. Such processes are characterized by the operations of batch processes generating periodic strong disturbances to the continuous processes and traditional regulatory controllers are unable to eliminate these periodic disturbances. ILMPC integrates the feature of iterative learning control (ILC) handling repetitive signal and the flexibility of model predictive control (MPC). By on-line monitoring the operation status of batch processes, an event-driven iterative learning algorithm for batch repetitive disturbances is initiated and the soft constraints are adjusted timely as the feasible region is away from the desired operating zone. The results of an industrial application show that the proposed ILMPC method is effective for a class of continuous/batch processes.

continuous/batch process, model predictive control, event monitoring, iterative learning, soft constraint

1 INTRODUCTION

Process industries can be divided into continuous and batch processes. Continuous processes are characterized by a steady stream of material through the plant and are usually operated in a steady-state manner. Batch processes are characterized by a prescribed processing of materials for a finite duration. Some processes, however, are composed of continuous and batch units, such as delayed coking units (DCU), pressure swing adsorption (PSA) [1], sequencing batch reactors (SBR), and simulated moving beds (SMB) [2]. For such processes, two tasks are usually concerned from the process control perspective. The first is the planning, scheduling, sequencing, and[3, 4]. The second is how to eliminate the periodic strong disturbances from batch operations. The main difference between the two tasks is whether some state variables or manipulated variables are discrete variables. In this paper, the second task is studied. The processes have the following characteristics. (1) Significant batch repetitive disturbances come from the batch operations and cyclically generated error persists batch after batch, which will not be compensated completely by the conventional proportional-integral-derivative (PID) controller or model predictive control (MPC). (2) The operation status of batch processes can be detected by on-line monitoring relevant variables.

Continuous process control tends to emphasize regulatory control around a fixed operating point or within a narrow operating region, which is acquired by optimizing certain economic performance under given operating conditions. The set-points should be tracked completely in order to maximize economic benefits. However, with the process restrictions, system constraints and disturbances, the optimal operating points are generally obtained by relaxing the constraints [5]. Especially for the class of continuous/batch processes, the batch processes bring about strong disturbances to the continuous processes, which may change the condition of the optimal steady state. The steady-state target thus has to be recalculated by steady-state optimization objectives.

Recently, MPC [6] has attracted the attention of industrial control engineers and academy, which is a technique with flexibility to handle constrained multivariable and non-square systems with time delays while permitting the use of several modeling forms. MPC is also certainly a helpful technique for the class of continuous/batch processes. MPC technology is originally developed to meet the special control requirement of power plants and petroleum refineries, and now it can be applied in a wide variety of areas including chemicals, food processing, automotive and aerospace [7, 8].

However, MPC has certain limitations in dealing with repetitive processes. The traditional MPC does not have the learning ability and can not make use of the knowledge and experience from the previous periodic operations. The repetitive way of periodic operations or disturbances allows the extraction of information from the past batches in order to improve the new batch. To exploit the repetitive nature of batch processes, the iterative learning control (ILC) is widely used [9, 10]. ILC refers to a body of methodologies that attempt to improve the control performance of a repetitive batch based on the results from previous batches and has been used originally in robotics because of their simplicity and effectiveness for repetitive processes [11]. Despite its comparatively matured conceptualization, the ILC theory is far from being perfect. For example, ILC can not include economically relevant optimization objectives. With the advantages of the MPC and ILC, a number of new formulations and extensions of ILC based on MPC have been proposed recently, greatly expanding the applicability of ILC. Lee. proposed Batch-MPC (BMPC) based on a time-varying multiple-input multiple-output (MIMO) linear model representing the underlying nonlinear batch process, attaining asymptotically perfect tracking despite initialization errors (or constant disturbances) and model errors [12]. Moreover, they presented a model-based iterative learning control algorithms that are tailored specifically for process control application [13]. Wang. combined an iterative learning control with a model predictive control for multi-phase batch processes [14]. Cueli and Bordons presented a new methodology, called iterative nonlinear model predictive control (INMPC) and showed an application to an uncertain pH plant [15]. These methods, however, impose a great computation burden, which are not realistic in practical applications. Tan. proposed a repetitive learning scheme incorporated into a predictive control scheme, but only provided the simulation results [16].

The objective of this study is to develop an iterative learning model predictive control (ILMPC) technique for a class of continuous/batch processes. An iterative learning scheme of batch repetitive disturbances is incorporated into model predictive control scheme. The proposed scheme is suitable to practical applications. An industrial application example will be demonstrated the feasibility and effectiveness of the proposed method.

2 SYSYTEM MODEL

For the class of continuous/batch processes, it is important that the process model is as simple as possible and is also a good representation of the process. On the other hand, the effect of batch operations must be considered and the relevant variables of batch units are integrated in the process model. As a consequence, the system model comprises general continuous process models and batch repetitive disturbances.

Given an open-loop stable MIMO system, the impulse response model of process input-output relationship can be identified through a test on an actual process. The model is expressed as

whereh,,y,,are the impulse response coefficient, system input, system output, settling time of the process, and the prediction horizon, respectively. Eq. (1) can be written in a vector form as

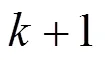
The corrected prediction model for the optimizer is reformulated as follows,

For the inevitable industrial modeling error, the open-loop predictive output has to be corrected. The closed-loop predictive model can be deduced from Eq. (4) as

The main difference between ILMPC and conventional MPC is that a disturbance learning scheme is incorporated into a predictive control scheme using an iterative learning approach. Therefore, a disturbance learning scheme is included in Eq. (5) to compensate the effects of both the state and output disturbances from batch operations. The disturbances from batch operations will be evaluated from previous cycles. The proposed iterative learning method can be easily applied in applications.

3 ILMPC FORMULATION

The ILMPC is realized in the predictive control algorithms on the basis of a process model by minimizing some selected performance index or cost function describing the control quality over the prediction horizon. The constraints are taken into account in the minimization, which may be presented in the manipulated variables and the outputs under operating conditions. For the class of continuous/batch processes, infeasibility problems arise with the strong batch repetitive disturbances and a feasible region is reconstructed by constraint softening.

In practice, the ILMPC formulation of the class of continuous/batch processes is divided into two pieces. The steady-state target calculation is used to obtain target values for each input and output, followed by a dynamic calculation to determine the most desirable dynamic trajectory to these target values. The ILMPC algorithm moves the plant from one constrained steady state to another, while minimizing the constraint violations in the process.

For the linear time invariant multivariable system, we assume that the steady state gain matrix exists, then the model of steady state process can be described by

Because the system constraints and disturbances result in infeasible solution for steady-state target calculation, a feasible region is almost always reconstructed by constraint softening [17]. It is the same for the class of continuous/batch processes. We formulate the slack soft constraint:

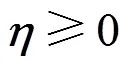
whereis the slack variable. Therefore, the target tracking optimization is formulated as the quadratic program [18]. There are some rather mature optimization techniques to solve the quadratic program, such as the active set method and the interior point method. The latter method is applied in this paper, and is as follows:

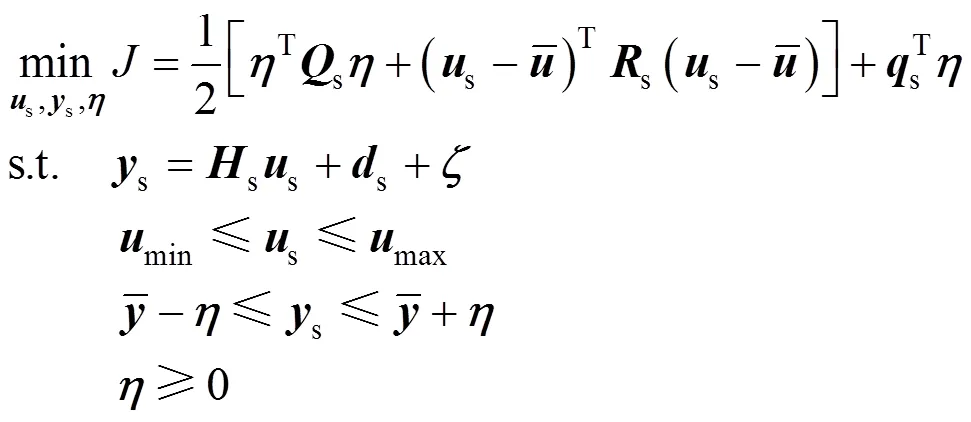
Given the calculated steady-state target (s,s), the regulator is formulated as the following dynamic optimal control problem.

Figure 1 Schematic diagram for a DCU

1—coker furnace; 2—coke drum; 3—fractionator; 4—light gas oil stripper; 5—heavy gas oil (HGO) stripper; 6—air cooler; 7—gas/oil separator; 8—condenser; 9—separator; 10—exchanger; 11—absorption column; 12—desorption column; 13—stabiliser; 14—reabsorber; 15—refluence tank

As showed above, an iterative learning scheme is incorporated into a predictive control scheme, which is applicable for the class of continuous/batch processes. The steady-state optimization provides controlled and manipulated variables set-points to the dynamic calculation, and it is executed at the same frequency as dynamic calculation. Both the steady-state optimization problem and dynamic calculation are translated into quadratic program problems. The quadratic program is in finite dimension and can be solved relatively easily and efficiently on-line at each time step by choosing both the control and predictive horizons to be finite [7]. On the other hand, the online computation burden is rather small for the iterative learning scheme of ILMPC. These characters of ILMPC areone of the main reasons for application of the algorithm.

到了台湾，除了看外景，就会跟她一起约着吃饭，两个人都安安静静的。那时候我还曾经去看过她的表演。我是坐在特别的包厢里面，在楼上的地方，她唱歌的时候，除了会看台底下的观众，也会往上看，我知道她在看我。我就坐在那边，看着台下的观众们为她用力地鼓掌呐喊，心里想，她是我的女朋友。当时外界并不知道我们在一起，看这场演出我也是没有等到结束就离开，在当时的台湾，如果被人拍到我们在一起，会是爆炸性的新闻。

4 CASE STUDY

4.1 Process description

The delayed coking is a thermal cracking process used in petroleum refineries to upgrade and convert petroleum residuum into liquid and gas products leaving behind a solid concentrated carbon material,.., petroleum coke. The DCU, in which the fresh feedstock is preheated, coked and fractionated, consists of one furnace, two coke drums, one main fractionator and absorption/stabilization units. A simplified diagram of a typical DCU is shown in Fig. 1. The vacuum resid from an upstream vacuum unit flows directly to the bottom section of the fractionator, where it is mixed with an internal reflux recycle of heavy cracked material. Then the total fresh and recycled feed is heated in the furnace. From the furnace, the resid flows to the bottom of one of the coke drums, where it continues to thermally crack to gas, gasoline, gas oil and coke. During the coking cycle, coke depositsin the active drum. The drum vapor products are separated into gas, raw gasoline, light and heavy gas oil in the main fractionator. The gas and raw gasoline are processed further in the absorption/stabilization units.

4.2 Batch characteristic analysis for the DCU

The DCU are typical continuous/batch processes. The furnace, fractionator and absorption/stabilization units are continuous processes, while coke drums are batch processes. The DCU have two identical coke drums, onstream and offstream. The coke remains in the drums and is periodically removed. It is the main reason that it is difficult to operate the coke drum. Once switched on, the drum goes through a cycle of steaming out, cooling, opening, coke removal, closing, steaming pressure testing, drum warm-up and coking. The filled coke drum is switched off twice daily for coke removal and then the empty drums are connected. Fig. 2 displays the production process of one of the two drums with 24-hour cycle period, which varies with different plants.

Figure 2 Coke drum operation cycle

By analysis of the process, we know that the events of drum switching, steaming out and drum warm-up operation cause more significant disturbances than others, which depriving the fractionator of both material and heat. Hence, the feed rate and composition of fractionator changes rapidly when the drum events occur. Not only the operation of fractionator but also the operation of downstream units are affected because of the propagated disturbances (such as fluctuations in fuel gas pressure and flow, and inlet temperature of furnace). Traditional regulatory controls are unable to eliminate these periodic transient disturbances, so that the plant is usually operated away from the optimum condition at a heavy economic toll. It is thus regarded that the DCU is one of the refinery units to be operated and controlled most difficultly due to its semi-batch nature [19].

4.3 Control strategy and industrial application

Periodic strong disturbances from batch operations (such as drum switching, steaming out, drum warm-up, and.) enter the system and may prevent the system reaching the desired steady state. Therefore, one of the key control objectives for the DCU is to stabilize the delayed coking operation in the constraints during the drum events. Fig. 3 (in the dotted line) shows the structure of ILMPC for the DCU. Local optimizers at each unit compute an optimal economic steady state and pass this information to the ILMPC for implementation.

Figure 3 The structure of ILMPC for the DCU

According to the characteristic of coking technology and operation experiences, we know that the drum events can be detected by on-line monitoring the top temperature, bottom temperature, pressure and their rate of change for the pair of drums. With the event monitoring scheme, a repetitive disturbance learning algorithm can be initiated timely by drum events [Eq. (3)].

For example, the discrete variable for detecting a drum switching event can be obtained, which is based on the change in the inlet temperatures of the two drums. The following conditions are matched simultaneously within the sampling time interval when a drum switching event occurs.

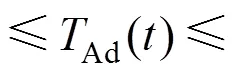
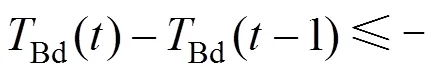
whereAdandBdare the bottom temperatures of the two drums. Subsequently, the response of the controlled variables to the drum event is obtained by disturbance learning scheme. For the illustration, the repetitive disturbance of the heavy gas oil draw temperature to the drum event is exemplified and shown in Fig. 4.

Figure 4 The response of the drum event

On the other hand, as the feasible region is away from the desired operating zone, the steady-state optimization will find new steady-state operating points as close as possible to the desired ones by Eq. (9). In this case, the soft constraints are adjusted and new steady targets are obtained and followed by a dynamic calculation, by Eq. (10).

The ILMPC for the DCU is based on the Distributed Control System (DCS) platform on which the ILMPC runs. The ILMPC runs once every one minute. The basic single-input single-output (SISO) control loopsare managed by DCS of the plant, which have fast dynamics compared with the ones of the whole process.

Figure 5 Comparison of control performance before and after ILMPC

Table 1 Averages and standard deviations of CVs before and after ILMPC

By the learning of the repetitive disturbance, better control performance is obtained after ILMPC, which can compensate the repetitive disturbances from the drum events. Fig. 5 shows the control performance before and after ILMPC with one cycle coking period of 24 h. Figs. 5 (a) and 5 (b) give the outlet temperature of furnace before and after ILMPC, respectively, indicating that ILMPC improves the control performance and reduces the regulation errors in the output. Before the ILMPC, the operators adjust the flow of fuel gas during drum events in order to reduce the influence of variance of furnace inlet temperature and gas pressure. Relative to the furnace and absorption/stabilization units, the main fractionator is affected most seriously by drum events. Figs. 5 (c) and 5 (d) show the control results for draw temperature of HGO and Figs. 5 (e) and 5 (f) for the overhead temperature of fractionator, before and after ILMPC respectively. Before ILMPC, the operators adjust intensively each reflux flow and the low/high feed ratio of fractionator in order to stabilize the operation of fractionator, resulting in poor control performance. With ILMPC, the fractionator operation fluctuates less and its key variables are kept within the desired operating range, providing better conditions for the smooth operation of the downstream units.

Table 1 shows the averages and standard deviations of the CVs from the data of one cycle period, comparing the systems without and with the proposed ILMPC control. ILMPC allows a closer approach to the limits. In all cases, the proposed ILMPC achieves more than 50% reduction for fluctuations.

5 CONCLUSIONS

In this paper, an ILMPC method for a class of continuous/batch processes is presented, in which batch repetitive disturbances enter continuous processes of the system and change the condition of the optimal steady state. Hence, the steady-state target received by the dynamic controller is recalculated in order to avoid poor control performance. An event-driven disturbance learning scheme is incorporated into the model predictive control. The ILMPC method is used in the delayed coking units, presenting better performance than a conventional method.

NOMENCLATURE

repetitive disturbance

ssteady value of measurable disturbance

model predictive error

transfer function matrix of

gtransfer function matrix ofg

ssteady state gain matrix

himpulse response coefficient

batch index

settling time of the process

prediction horizon

symmetric weighting matrix

ssymmetric positive definite matrix

symmetric weighting matrix

ssymmetric positive definite matrix

Adbottom temperature of drum

Bdbottom temperature of drum

ssampling time

system input

future control vector

gpast control vector

maxmaximization of the manipulating variables

minminimization of the manipulating variables

ssteady values of manipulating variables

measured output

ysystem output

predictive output vector

rreference trajectory

ssteady values of controlled variables

parameter of reference trajectory

learning gain matrix

deviation between predictive output and current output

slack variable

error correction vector

time constant of reference trajectory

1 Zeng, R., Guan, J.Y., “Progress in pressure swing adsorption models during the recent 30 years”,...., 10 (2), 228-235 (2002).

2 Huang, L., Sun, L., Wang, N., Jin, X.M., “Multiobjective optimization of simulated moving bed by tissue P system”,...., 15 (5), 683-690 (2007).

3 Sarabia, D., De, P.C., Cristea, S., “Hybrid predictive control of a simulated continuous-batch process”, In: Proceedings of the 16th IEEE International Conference on Control Applications, Singapore, 1400-1407 (2007).

4 Shaw, K.J., Lee, P.L., Nott, H.P., Thompson, M., “Genetic algorithms for multiobjective scheduling of combined batch/continuous process plants”, In: Proceedings of the IEEE Conference on Evolutionary Computation, California, USA, 293-300 (2000).

5 ZOU, T., LI, S.Y., “Constraints adjustment and objectives coordination of satisfying optimal control applied to heavy oil fractionators”,...., 13 (3), 380-387 (2005).

6 Camacho, E.F., Bordons, C., Model Predictive Control, Springer, New York (2004).

7 Morari, M., Lee, J.H., “Model predictive control: Past, present and future”,..., 23 (4/5), 667-682 (1999).

8 Qin, S.J., Badgwell, T.A., “A survey of industrial model predictive control technology”,.., 11 (7), 733-764 (2003).

9 Xu, J.X., Tan, Y., Linear and Nonlinear Iterative Learning Control, Springer-Verlag, Berlin (2003).

10 Lee, J.H., Lee, K.S., “Iterative learning control applied to batch processes: An overview”,.., 15 (10), 1306-1318 (2007).

11 Arimoto, S., Kawamura, S., Miyazaki, F., “Bettering operation of robots by learning”,., 1 (2), 123-140 (1984).

12 Lee, K.S., Chin, I.S., Lee, H.J., Lee, J.H., “Model predictive control technique combined with iterative learning for batch processes”,., 45 (10), 2175-2187 (1999).

13 Lee, J.H., Lee, K.S., Kim, W.C., “Model-based iterative learning control with a quadratic criterion for time-varying linear systems”,, 36 (5), 641-657 (2000).

14 Wang, Y., Zhou, D., Gao, F., “Iterative learning model predictive control for multi-phase batch processes”,, 18 (6), 543-557 (2008).

15 Cueli, J.R., Bordons, C., “Iterative nonlinear model predictive control. Stability, robustness and applications”,.., 16 (9), 1023-1034 ( 2008).

16 Tan, K.K., Huang, S.N., Lee, T.H., Tay, A., “Disturbance compensation incorporated in predictive control system using a repetitive learning approach”,, 56 (1), 75-82 (2007).

17 Kassmann, D.E., Badgwell, T.A., Hawkins, R.B., “Robust steady-state target calculation for model predictive control”,., 46 (5), 1007-1024 (2000).

18 Rao, C.V., Rawlings, J.B., “Steady states and constraints in model predictive control”,., 45 (6), 1266-1278 (1999).

19 Haseloff, V., Friedman, Y.Z., Goodhart, S.G., “Implementing coker advanced process control”,, 86 (6), 99-103 (2007).

2009-03-12,

2009-10-12.

the National Creative Research Groups Science Foundation of China (60721062) and the National High Technology Research and Development Program of China (2007AA04Z162).

** To whom correspondence should be addressed. E-mail: sqwang@iipc.zju.edu.cn