A Strategy for the Integration of Production Planning and Scheduling in Refineries under Uncertainty*
LUO Chunpeng (罗春鹏) and RONG Gang (荣冈)**
A Strategy for the Integration of Production Planning and Scheduling in Refineries under Uncertainty*
LUO Chunpeng (罗春鹏) and RONG Gang (荣冈)**
State Key Lab. of Industrial Control Technology, Institute of Cyber System and Control, Zhejiang University, Hangzhou 310027, China
A strategy for the integration of production planning and scheduling in refineries is proposed. This strategy relies on rolling horizon strategy and a two-level decomposition strategy. This strategy involves an upper level multiperiod mixed integer linear programming (MILP) model and a lower level simulation system, which is extended from our previous framework for short-term scheduling problems [Luo, C.P., Rong, G., “Hierarchical approach for short-term scheduling in refineries”,...., 46, 3656-3668 (2007)]. The main purpose of this extended framework is to reduce the number of variables and the size of the optimization model and, to quickly find the optimal solution for the integrated planning/scheduling problem in refineries. Uncertainties are also considered in this article. An integrated robust optimization approach is introduced to cope with uncertain parameters with both continuous and discrete probability distribution.
refinery, planning and scheduling, optimization model, simulation system
1 INTRODUCTION
To compete successfully in international markets, oil refineries are concerned with improving the planning and scheduling of their operations to achieve better economic performance. Many progresses have been achieved on planning and scheduling in refineries [1-13], and commercial softwares, such as RPMS, PIMS and ORION, for refinery production planning and scheduling have facilitated the development of general production plans and schedules of the whole refinery. Linear programming is a good technique for production planning of refineries. However the short-term scheduling problem is still one of the most challenging problems in operational research due to the complexity of the scheduling operations and the corresponding process models. In addition, the integration of planning and scheduling has received less attention because of the major challenges toward dealing with the different time scales and the problem size of the resulting optimization model.
To meet the challenge in the short-term scheduling, many scheduling models and solution strategies, such as scheduling models with discrete time formulation, scheduling models with continuous-time formulation, decompose strategies, heuristic algorithms, and simulation and expert systems, have been proposed in literature [1-13]. When a model is described with discrete time, the time slot duration must be short enough to honor all the operation rules and the variables during the whole scheduling horizon will increase dramatically. Pinto and Joly [9] had defined a time slot duration of 15 minutes for crude oil scheduling problems, which generated a discrete time mixed integer optimization model with 21504 binary variables in a 3-4 days horizon. They pointed out that the solution of such a problem is far beyond the capabilities of the current optimization technology. The continuous-time modeling is particularly suitable for scheduling problems with activities ranging from a few minutes to several hours. Because of the possibility of eliminating a major fraction of the inactive event-time interval, the resulting mathematical programming problems are usually of much smaller sizes and require less computational efforts for their solution [2, 3, 6]. However, due to the variable nature of the timings of the events, it becomes more challenging to model the scheduling processes and the continuous-time approach may lead to mathematical models with more complicated structures compared with their discrete-time counterparts.
Some other authors have resorted to intelligent simulation systems to deal with scheduling problems. Paolucci and Sacile [11] used a simulation-based decision support system (DSS) to improve the effectiveness of the decisions on allocating crude oil supply to port and refinery tanks. Chryssolouris and Papakostas [12] used an integrated simulation-based approach to evaluate the performance of short-term scheduling with tank farm, inventory and distillation management. The use of simulation model to provide decision support can allow the application of public domain of heuristic knowledge, support what-if analysis and be able to evaluate the performance of alternative solutions. But simulation systems rely on the user to specify the independent variables,.., flows into and out of a unit over time. The simulator can then calculate the dependent variables such as a tank’s holdup and quality at each time interval. The values of those independent variables are mainly dependent on scheduler’s experience and can’t ensure optimal schedules.
Although many progresses have been achieved on planning and scheduling in refineries, the integration of planning and scheduling has received less attention. Two of the major challenges towards this integration are dealing with the different time scales and with the problem size of the resulting optimization model [14-17].
Regarding the time representation, one approach is to define a very large scheduling problem that spans the whole planning horizon and, to define longer lengths for future time periods to yield a formulation where the immediate future includes more details than the distant future. This approach always generates a model that can not be solved in the full space due to its size and that some type of decomposition is required [14, 15]. The second approach is to define an aggregate planning problem and a detailed scheduling problem with equivalent horizon, and information is passed from the planning model to the scheduling model [14, 16]. A third method for dealing with the different time scales is to use a rolling horizon approach where only a subset of the planning periods include the detailed scheduling decisions with shorter time increments. The detailed planning/scheduling period moves as the model is solved in time [14, 17]. When such a planning/scheduling model is solved in real time, the first planning period is often a detailed scheduling model while the future planning periods include only planning decisions and this approach is mainly used in this study.
Because of the challenge in the computation of the integrated planning/scheduling problem, a framework is introduced in this article. This framework is an extension of our previous study, which involves two decision levels for short-term scheduling problems in refineries: an optimization model at the upper level and a simulation system at the lower level. The main purpose of the approach is to reduce the binary variables and the size of the optimization model caused by the representation of multipurpose tanks in refineries and operation rules for material movements. The optimization model is used to decide when, how long, and how much an operation (operation mode) is active and, also, to determine how many materials (raw materials, intermediate materials, and final products) are produced and consumed by the operations. In this optimization model, only operation modes of processing units, blenders, and pipelines are considered. Although this model is based on discrete time formulation, we use the methods mentioned by GÖthe-Lundgren and Lundgren [4] to extend the model and allow the start and end of each operation mode at any point in a time slot. Another characteristic of the optimization model is that only aggregate tanks are used, and that each kind of material [2, 3, 6] has only one aggregate tank. The details of material movements between all actual units (including individual tanks) will be determined in the simulation system at the lower level. The simulation system uses some heuristics and rules to arrange actual tanks to receive/send materials with logic operation constraints (operation rules) on respective tanks. The maximum storage capacities of aggregate tanks can be violated in the optimization model, and this strategy is used to model the multipurpose tanks, which can hold different materials in different operation modes. The simulation system uses a heuristic to try to eliminate the extra capacity requirements of these aggregate tanks. The iteration procedure between the upper level and the lower level can be used to find optimal solution under updated aggregate storage capacities. With the cooperation of the simulation system, the upper level optimization model only needs to make macro decisions, and the time slot does not need to be short enough to honor all the operation rules. Just for this reason, we believe that the upper level model can be easily transformed to an integrated planning/scheduling optimization model, and that the simulation system can still be a good tool for the detailed decision-making during the scheduling horizon.
Uncertainties are also considered in our integratedplanning/scheduling model. Generally, stochastic models under uncertainty can be divided into two categories depending on whether it follows the scenario-based framework. When the uncertain parameters follow continuous probability distribution, one usually generates a finite set of scenarios, from sampling or a discrete approximation of the given distributions, to represent the probability space [18]. As the number of uncertain parameters increases, more scenarios must be considered, which results in a much larger problem. This main drawback that limits the application of these approaches is to solve practical problems with various uncertain parameters. Stochastic models not following scenario-based framework have also been applied to scheduling problems, and probabilistic (chance) programming, fuzzy mathematical programming, probabilistic programming, and flexible programming are important approaches of non-scenario- based framework [19].
In this article, we integrate the robust optimization approach presented by Janak et al. and Leung et al., to cope with the uncertain parameters with both continuous and discrete probability distribution respectively [20, 21].
2 ARCHITECTURE OF THE STRATEGY
In this study, the hierarchical approach of our previous framework for short-term scheduling in refineries is extended, which includes a mathematical programming model at the upper level and a simulation system at the lower level [22]. The upper level optimization model is now changed to an integrated robust planning/scheduling model. A time representation called rolling horizon mode is adopted to address the integrated planning/scheduling optimization strategy in refineries. The planning horizon (1 to 3 months) is divided into a certain number of planning periods (weeks). Only the first planning period includes the detailed scheduling decisions with shorter time increments (days), and only those decisions belonging to the first planning period are passed to the simulation system at the lower level. At the end of the first planning period, the state of the system is updated, and the computational cycle is repeated with the horizon advancing one period by one period.

Figure 1 Time representation of our approach
The mathematical scheduling model in the first planning period is based on discrete time formulation with 1 day increment for each scheduling period. This scheduling model is used to decide sequencing and timing of the operation modes of units and to determinethe quantities of materials consumed/produced by each operation mode of a unit. Although this is a scheduling model, it does not consider the operation details of each individual tank. Only aggregate tanks are considered in this model, and an aggregate tank is used only for one kind of material. And the operation rules related to material movements for each individual tank are not considered in this model. The storage capacity of an aggregate tank is the sum of the storage capacities of individual tanks storing the same material.
It is well-known that there exits multipurpose tanks in refineries, and they can be used to store different materials when their operation modes are changed. An aggregate tank may possess some multipurpose tanks, so the storage capacity of an aggregate tank may change depending on which operation modes the multipurpose tanks will be in.
To model the alterable storage capacity of each aggregate tank, the maximum storage capacities of aggregate tanks can be violated by using some slack variables which are punished by penalties in the mathematical model. And the value of each slack variable, which is called the extra capacity requirement of an aggregate tank, represents the degree to which the current maximum storage capacity of a corresponding aggregate tank cannot satisfy the demands of production.
The planning model beyond the first planning period is similar to the scheduling model. The main difference is that the planning period (1 week) is longer than the scheduling model (1 day), and the planning model is only used to determine which operation is active and how long an operation is active during each period. So the tight constraints, such that each unit can at most be in one mode during a period, are relaxed in the planning model. And, some operation details considered in the scheduling model, such as modeling the changeover of operation modes between two adjacent periods, and modeling the variety of the charge size of each unit between two adjacent periods, are ignored in the planning model. In the planning model, aggregate tanks are the same as those in the scheduling model, and the maximum storage capacities of aggregate tanks can also be violated.
Because slack variables are used in the upper level optimization model to represent the extra storage capacity requirements of aggregate tanks, one important role of the simulation system at the lower level is trying to eliminate the extra capacity requirements by adjusting the operation modes of the multipurpose tanks within some aggregate tanks that have redundant capacities. Once the upper level model finds an optimal solution without extra storage capacity requirements, another important role of the simulation system is to determine detailed operations for each individual tank with operation rules considered. These decisions involve arranging the sequence and the time point that each individual tank receives/sends materials. Some heuristics are used in the simulation system to deal with these tasks.
The strategies, involving the mathematical representation of multipurpose tanks and the operation rules for material movements related to each individual tank are ignored in the mathematical model, can reduce a large number of binary variables and the size of the integrated planning/scheduling model. This can help the model to find the optimum solution within a reasonable time.
The solution strategy for the integrated planning/ scheduling decisions of refineries involves an iteration procedure between the integrated planning/scheduling optimization model and the simulation system. The iteration procedure is shown in Fig. 2. When the integrated planning/scheduling optimization model finds an optimal solution, the variables in the first planning period, which are scheduling decisions, are taken as inputs in the simulation system at the lower level. The lower level then first tries to eliminate the extra capacity requirements by adjusting the operation modes of the multipurpose tanks within some aggregate tanks that have redundant capacities. When the simulation system adjusts the operation modes of some multipurpose tanks, the storage capacities of the corresponding aggregate tanks will be changed. Then the updated storage capacities will be feed back to the mathematical model at the upper level, and the integrated planning/scheduling optimization model will be recalculated to find the new optimal solution. The variables in the first planning period of this new optimal solution are again taken as inputs in the simulation system, and then the simulation system try to eliminate the new extra capacity requirements. So, there is an iterative link between the upper lever and the lower level.
If the simulation system at the lower level cannot find redundant storage capacities, the maximum storage capacity constraints at the upper level must be changed to hard constraints that cannot be violated. The optimization model will be recalculated with hard constraints. The iteration procedure of our approach is shown in Fig. 2 and the termination conditions of the iteration procedure can be referred from our previous work [22].
After the termination of the iteration procedure, if an optimal solution is found, the simulation system will continue to use heuristics to determine the detailed material movements related to each individual tank in the first planning period.
Because rolling horizon mode is adopted, only the first planning period includes the detailed scheduling decisions and only these decisions belonging to the first planning period are passed to the simulation system at the lower level. The extra capacity requirements beyond the first planning period show the shortage of the storage capacities in the future, but they will not be inputted to the simulation system in the current time. When the horizon advances, they will be dealt with one period by one period.
Since our upper level model is for long-term planning/scheduling problem, its uncertainty is also considered. In this article, properties for components entering blending units are uncertain parameters with continuous probability distribution, and demands for final products in the scheduling horizon are uncertain parameters with discrete probability distribution. The integrated planning/scheduling model with these uncertain parameters is converted to determinative model by integrating the robust approaches proposed by Janak. and Leung[20, 21]. The approach of Janak. can avoid enumerating scenarios for uncertain parameters following continuous probability distribution, but it has the difficulty of dealing with uncertain parameters following discrete probability distribution [20]. However, the approach of Leung. can deal with uncertain parameters following discrete probability distribution by enumerating scenarios [21]. In this article, we integrate the robust optimization approach presented by Janak. and Leung. to cope with the uncertain parameters with both continuous and discrete probability distribution.
3 An Overview of Robust Optimization
3.1 Scenario-based robust optimization
The robust optimization, presented by Leung., integrates a goal-programming formulation with a scenario-based description of input data [21]. The model generates a series of solutions that are progressively less sensitive to the realizations of input data from a set of scenarios.

Figure 2 Iteration procedure of our approach
Letbe a vector of the design variables that cannot be adjusted once a specific realization of the data has been observed, and letbe a vector of control variables that are subject to adjustment once uncertain parameters are observed. Then the form of their robust optimization model is as follows:
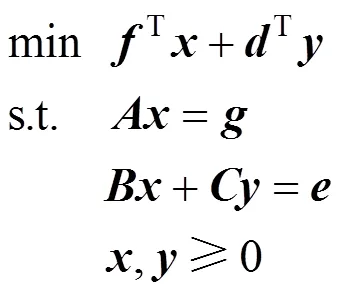

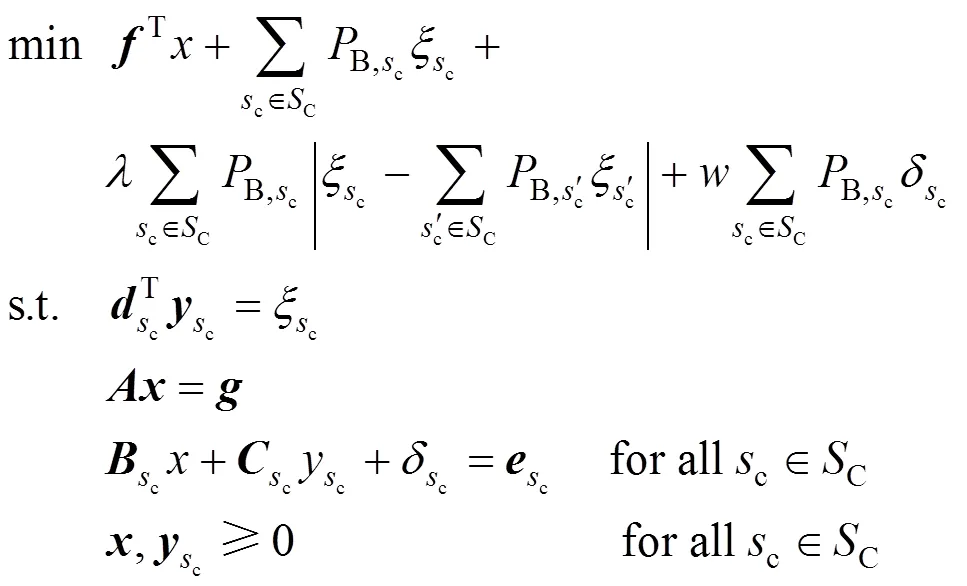
3.2 Non-scenario-based robust optimization
Janak. assumed that the uncertainty may arise from both the coefficients and the right-hand-side parameters of the inequality constraints, and the uncertainty may also arise from the coefficients of objective function [20]. Thus, the feasibility of the following inequality is concerned.
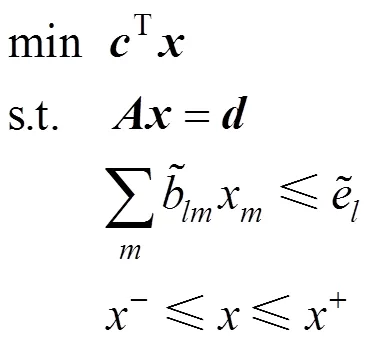
Assuming that the true values of the uncertain parameters are obtained from their nominal values by random perturbations:

In this situation, solutionis called robust if it satisfies the following:
(i)is feasible for the nominal problem, and
(ii) the probability of violation of the uncertain inequality with an error is at most:


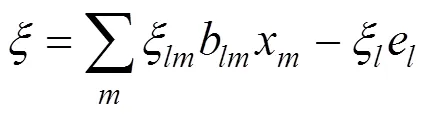
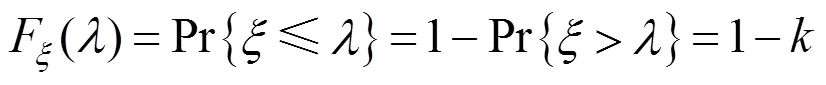
The final form of the deterministic constraint (or robust counterpart problem) is simply determined using the inverse distribution function of the random variable. Let

then we can get the deterministic constraint:
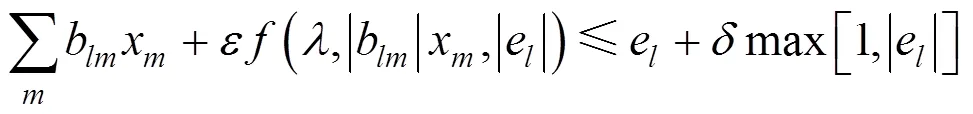
4 INTEGRATED PLANNING/SCHEDULING MODEL
The proposed model divides the planning horizon(1-3 months) into periods of length1(1 week) where production is planned using both known and estimated demands. The first planning period of the time horizon is divided into time intervals of lower length2(1 day). The model is to be rerun every period1as forecasts become real orders. In the model, demands for some final products in the first planning period are random parameters with discrete probability distribution, which represents the fluctuation of arrival time of vehicles that transport products. However, the properties for components entering the blenders are all random parameters with continuous probability distribution during the whole planning horizon.
The optimization model is a MILP model based on discrete time. The flow sheet of a refinery studied is the same as our previous work, as shown in Fig. 3. The figure consists of a set of rectangles/triangles that represent the units/tanks in the plant and “connections” which represent the flow paths between equipments. The small squares connected to the equipment by short lines are the “ports” where flow enters or leaves the equipment. The pentagons represent the “perimeter” (equivalent to pipelines) through which materials entering/leaving the plant. The ports of perimeters are not shown in the figure for simplification. Supply orders or demand orders can be defined on the perimeters. The description of the flow sheet in Fig. 3 is based on the works of Kelly and on Honeywell Process Solutions called “Honeywell Production Scheduler”, and the modeling data is provided by a refinery of PetroChina where “Honeywell Production Scheduler” has been implemented [23, 24].
4.1 Constraints of the scheduling model in the first planning period
Some constraints are similar to our previous study, it is not presented here and more details can be obtained from our previous work [22] and Appendix A. The following constraints are only the important constraints that can help to understand the strategies adopted in this study.
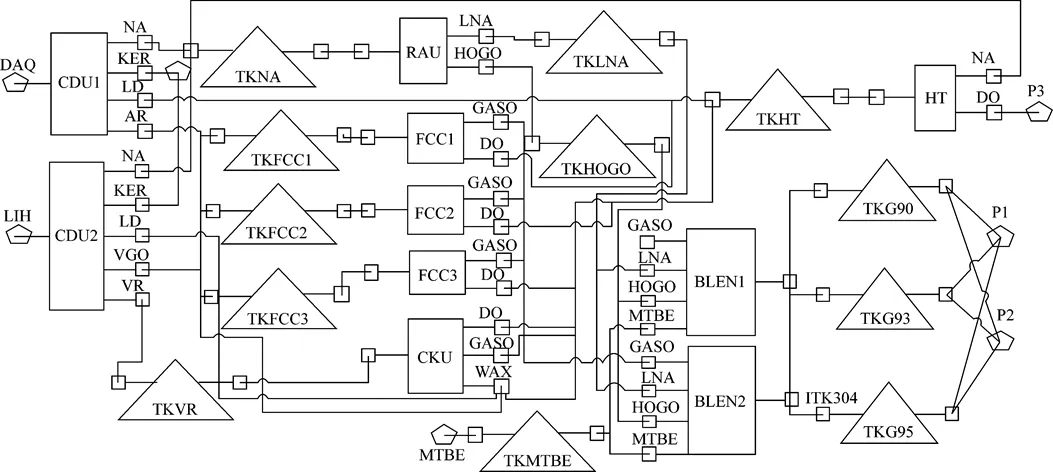
Figure 3 Simplified flow sheet of a refinery
():



:


:


Constraints (12) and (13) specify that the minimum and maximum capacity of each aggregate tank must be satisfied if there are no other storage capacities that can be adjusted to extend the current storage capacity. Otherwise the maximum storage capacity can be violated as shown by (14) and (15). Constraints (13) and (15) are used for products with random demands.
:
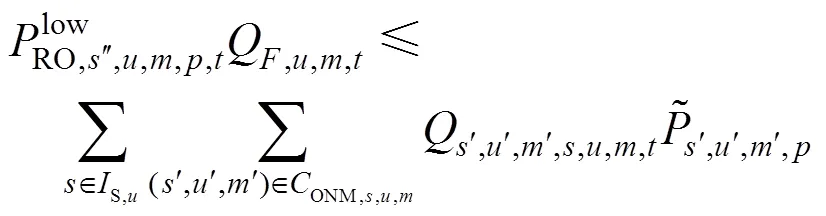

These constraints are used to blenders only. The properties of the product leaving the outflow port (each blender only has one outflow port) can be directly predicted by using a volumetric average, and, constraint (16) specifies that propertyof the flow leaving the outflow port must satisfy the minimum and maximum specifications. In this article, we assume that the properties of the flows entering the blenders are random parameters with continuous probability distribution. The blending index for each of the different nonlinear qualities is used to convert each of the nonlinear qualities to a linear index that may be blended linearly by volume.
Let the reliability level for this uncertain constraint be, and assume that the true value of each uncertain property of component is obtained from their nominal values by random perturbations, which is shown as follows:

Then the deterministic robust counterpart problem of (17) is (18).

:


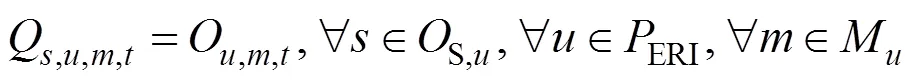
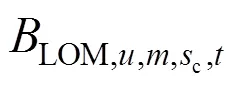
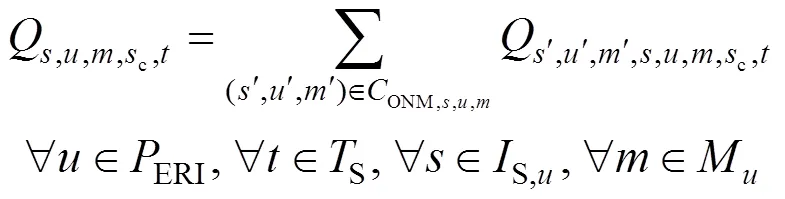
4.2 Constraints of the planning model beyond the first period
The time period in the planning model is 1 week. We assume that the random demands in the first planning period will at most influence the production to the end of the second planning period. So the inventory for these products with random demands will be design variables at the end of the second period, which cannot be adjusted once uncertain demands have been observed. Thus, Constraint (10) is changed to:
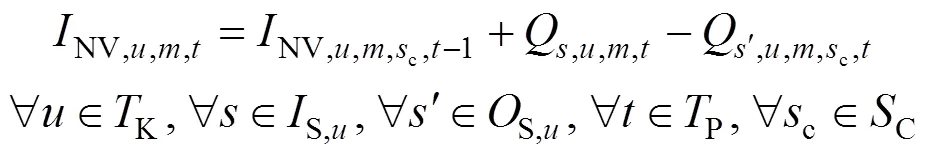
In the planning model, the maximum capacity of each aggregate tank also can be violated using soft constraints as (12). However, the extra capacity requirements beyond the first planning period are not adjusted by the simulation system in the current time, and they will be adjusted one period by one period as the horizon advances. To ensure that the solution beyond the first planning period is as feasible as possible, the maximum capacity of tank farms that the aggregate tanks belong to cannot be violated, shown as follows:

The demands beyond the first planning period will be unknown and be estimated, and the estimated minimum and maximum demands for each product are defined on the outflow perimeters. Constraints (19)-(21) are changed as follows:



Constraint (26) is only used in the second period.
In the planning model, detailed operational rules considered in the scheduling model are ignored. For example, constraints, such as modeling the changeover of operation modes between two adjacent periods, modeling the variety of the charge size of each unit between two adjacent periods, and that each unit can at most be in one operation mode during one period, can be ignored to allow more than one operation mode during one planning period. Finally, constraints (12), (14), (18), (23)-(27), as well as constraints (A-1)- (A-4), (A-9), (A-10) in Appendix A, constitute all the planning constraints beyond the first period.
4.3 Objective function
The main objective of the integrated scheduling/ planning problem is to maximize the profits of products and minimize all kind of penalties. The objective function is as follows:


5 The Simulation System at the Lower Level
The simulation system at the lower level is the same as that in our previous study. Several heuristics are used in the system, and the simulation system serves five objectives: (1) to try to adjust the operation modes of multipurpose tanks within the aggregate tanks to change storage capacities of some aggregate tanks, (2) to construct a schedule including detailed material movements related to each individual tank, (3) to evaluate the performance of alternative schedules obtained by the experience of schedulers, (4) to generate detailed scheduling orders to workshops, and (5) to evaluate the effects on production when production fluctuation and unpredicted events occur. More details about the simulation system can be obtained from our previous work [22].
6 Computation Results
Several cases are studied based on the flow sheet shown in Fig. 3. The flow sheet is composed of an atmospheric distillation column (CDU1), an atmospheric distillation column combined with a vacuum distillation column (CDU2), three fluidized catalytic cracking units (FCC1, FCC2, FCC3), a delaying coke unit (CKU), a hydrotreatment unit (HT), a reforming unit (RAU), two blenders (BLEN1, BLEN2), twelve aggregate tanks, three inflow perimeters and four outflow perimeters. Atmospheric distillation fractionates crude oil into the following hydrocarbon streams: naphtha (NA), kerosene (KER), light diesel (LD) and atmospheric residue (AR). The vacuum distillation column fractionates the AR stream into two streams: vacuum gas oil (VGO) and vacuum residue (VR). FCC unit produces a gasoline component (GASO) and diesel oil (DO). Reforming unit (RAU) produces light naphtha (LNA) and high quality gasoline component (HOGO). CKU produces a gasoline component (GASO), diesel oil (DO) and wax oil (WAX). Material MTBE is used to improve the quality of gasoline products. HT improves diesel oil quality by reducing the sulfur content. The 90# gasoline, 93# gasoline, 95# gasoline can be blended by each blender. Two different crude oils DAQ and LIH are supplied to CDU1 and CDU2 respectively. The minimum capacity (LB) and maximum capacity (UP) for each unit and the initial inventory (INIVF) for tanks are shown in Table 1. The unit of each minimum capacity, maximum capacity, and initial inventory for the tanks is cubic meters. Otherwise the unit is cubic meters per hour. The actual tanks in TKG90, TKG93, and TKG95 are all multipurpose tanks, and the data of the actual multipurpose tanks in TKG90, TKG93, and TKG95 are shown in Table 2.

Table 1 Capacity data and initial inventory
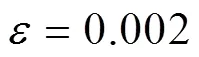

Table 2 Multipurpose tanks in aggregate tanks

Table 3 Property data of materials entering the blenders
The two blenders (BLEN1and BLEN2) and perimeters P1 and P2 all have three operation modes: G90 (90# gasoline mode), G93 (93# gasoline mode) and G95 (95# gasoline mode). They can only transfer material to/from one aggregate tank in one operation mode. For example, BLEN1 in operation mode G90 can only send material to TKG90, and P2 in operation mode G93 can only receive material from TKG93. The specifications on octane value of the products leaving the blenders in different modes are shown in Table 4.
A planning horizon of 1 month with 1 week for each planning period is used for these cases, which have in total ten time slots: seven time slots for the first planning period and three time slots for the other planning periods. The penalty for the inventory and the penalty for the extra storage capacity requirement are 1. The other penalties are all 10. We assume that some demand for product G93 with the quantity of 2640 in time slot 4 is uncertain, and this demand may arrive at the plant with the probability 0.8 in time slot 4, 0.1 in time slot 3, and 0.1 in time slot 5, which depends on the arrival time of the vehicles. Correspondingly, there are three scenarios in the robust model. The orders defined on each perimeter unit are shown in Table 5. In the first period, each order specifies quantities of demands/supplies and the time horizon of demands/supplies. And beyond the first period, each order specifies the minimum and maximum quantities of demands/supplies and the time horizon of demands/ supplies. The UNIT and MODE shown in Table 5 represent the materials transferred by the unit in that mode. ST and ED represent the start time slot and end time slot in which the materials can be transferred. LB and UP represent the minimum and maximum quantities that can be transferred by each day between periods ST and ED. Demands for product G93 from time slot 1 to time slot 5 are the nominal demands.

Table 4 Specifications on octane value of gasoline products

Table 5 Orders defined on each perimeter
The integrated scheduling/planning robust model with uncertain data was implemented in LINGO 9. The calculations were performed on a Celeron(R) 2.40 GHz/512Mb RAM platform. The model involves 380 discrete variables, 12000 continuous variables, and 11394 single constraints. The CPU time required for the solution of the model is 223s, and objective value is 627888000.
Only the maximum storage capacity of aggregate tank TKVR is violated. The inventory level and the extra capacity requirement in each period are shown in Table 6. To eliminate the extra capacity requirements of TKVR in the first planning period, the simulation system at the lower level selects Tank3 in aggregate tank TKG93 to extend the maximum storage capacity of TKVR. By this adjustment, the maximum storage capacity of TKVR and TKG90 change to 28000 and 24000 m3, respectively. The CPU time required for the solution of the updated MILP model is 220 s, and the value of the objective function is 627923900. There are no tanks with the maximum capacities violated are found in the new solution for the first period, and the iteration procedure terminates. But there are still extra capacity requirements for TKVR beyond the first planning period (the first seven time slots), and they will be adjusted one period by one period as the horizon advances. The extra capacity requirements for TKVR after the adjustment are also shown in Table 6.

Table 6 Inventory in TKVR and the extra storage capacity requirement in each time slot
The penalties defined in this model are subjective, and a series of cases are used to test the influence of the penalties on the solution. Three kinds of penalties are considered, which are the penalty for extra storage capacity requirement, the penalty for inventory, and the penalty for changeover of operation modes. It is found that the value of the objective function will decrease with the increase in penalties. When the penalties for extra storage capacity requirements take the values between 1 and 10000, the solutions are all the same. This means that this kind of penalties will have no influence on the production decisions when they are between 1 and 10000. When the penalties for changeovers of modes are greater than 50, the solutions of our model keep constant. However, the modes of the blenders change more frequently when this kind of penalties are less than 50. It is found that the solution will also keep constant when the penalties for inventory take the values between 1 and 10000. In a real case, if the holding cost for inventory and the cost for changeover are known, these penalties can be equal to the cost. If these costs are not known, it is suggested that these penalties should be as small as possible. So the penalties for extra storage capacity requirements, for changeovers of modes, and for inventory, should take the values of 1, 50, and 1 respectively in our model. In a real case, the values of penalties may also be used depending upon the decision makers’ goals and the specific nature of the problems.
To compare with the results of a model with nominal data, a “nominal” model is built. The CPU time required for the solution of the model is 144 s, and objective value is 630405600. In each period, the inventory level for TKVR of the nominal model is the same as that of the robust model, and the case is the same for the extra capacity requirements of this tank. The simulation system still select Tank3 in aggregate tank TKG93 to extend the maximum storage capacity of TKVR. The CPU time required for the solution of the updated MILP model is 142 s, and the value of the objective function is 630441500. The property values for the products in both the “nominal” model and the robust model are shown in Table 7. It is found that the property value for each product always reaches the upper bound of the property specification in the “nominal” model. This means that the upper bound of the property specification will be easily violated by the fluctuation of the property for each component. However, the property for each product in the robust model is close to the center between the lower bound and the upper bound, which means that it is more robust when the property of each component fluctuates.
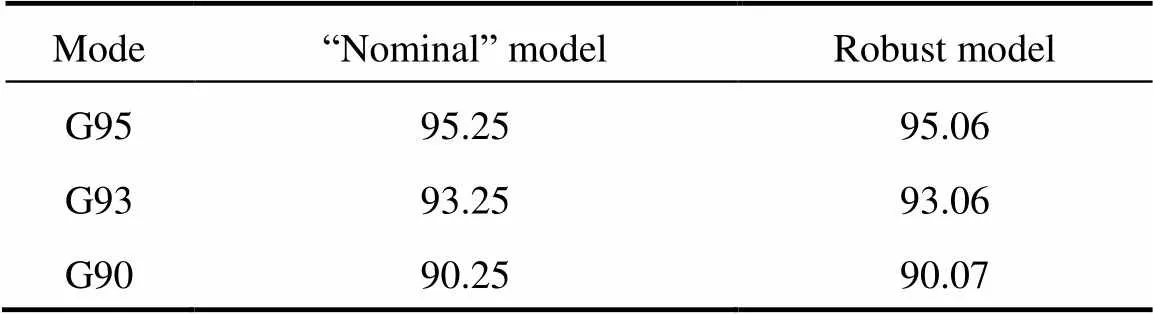
Table 7 Property of gasoline products produced in each model
The quantities of product G93 produced in each time slot for the “nominal” model and the robust model are shown in Table 8. The total production during each period in Table 8 represents the total quantities produced from time slot 1 to the current time slot. It can be seen that the total amounts in time slot 5 for each model are the same. This means that the two models produce the same amount of product G93 during the first five time slots. However, the total quantities in the robust model in time slot 2, 3, and 4 are greater than that in the “nominal” model. This is caused by eliminating the influences of the fluctuated demands for G93 from time slots 3 to 5.


Table 8 Amount and total amounts of product G93 produced in each model
To test the influences of various parametersandon the model, the maximum production capacities of blenders BLEN1 and BLEN2 are set to 200 and 100, respectively. At the same time, the inventory for tank TKG93 at the beginning of time slot 1 is set to 0. The demands of product G93 will not be satisfied by these adjustments. In this case, the change ofandstill has no influences on the values of all the variables in the results except whengets value 0. The value of the objective function will decrease withincreased. And the value of the objective function keeps constant whenchanges. That parametersandhave no influences on the solution may be caused by our modeling strategy and model structure.
To compare with our approach, a monolithic integrated planning/scheduling optimization model with a planning horizon of 3 months is built. And another four operation modes are added to each of unit CDU1, CDU2, FCC1, FCC2 and FCC3. We refer to the study of Shah [25] to model the multipurpose tanks. During the whole planning horizon, each multipurpose tank within TKG90, TKG90 and TKG95 has four operation modes G90, G93, G95 and VR. Moreover, during the scheduling horizon, the flows leaving each outflow port of unit BLEN1 and BLEN2 can at most move to two of these multipurpose tanks and each of P1 and P2 can receive materials from at most two of these multipurpose tanks. This model involves 1927 discrete variables, 39742 continuous variables and 37647 single constraints. Even the first feasible solution of this model cannot be found within 10000 s. However, our approach for this problem involves only 990 discrete variables, 38626 continuous variables and 35901 single constraints. The CPU time required for the optimal solution of this MILP model is only 4836s.
The time needed to find the optimal solution depends on the size of the optimization model and the number of binary variables in this model. Three main factors influence the model size and the number of binary variables. The first is the number of units involved in the model. The second is the number of operation modes each unit possesses. The third is the number of periods adopted in the model. According to our tests, when more units without multimode operations and more blending properties are considered in the mode, the computational time does not change significantly. The reason is that no more discrete variables are created. However, when the added units have more than one operation modes, the computational time will have a remarkable change. For example, we add the following units and properties to the last model: 20 additional types of crude oils with 20 aggregate tanks, four crude oil blenders with 5 operation modes for each, two additional vacuum distillation columns with 5 operation modes for each, two additional product blenders with 5 operation modes for each, 5 additional products with 5 aggregate tanks, and 7 additional properties needed to be controlled. When these new added units are confined to only one operation mode, the computational time is 5141 s, which is 305 s more than 4836 s. However, if the operation modes are not confined, the computational time is 12155 s. This remarkable change in time is caused by much more discrete variables in this model. To control the number of binary variables and the size of the optimization model, some strategies can be used. For example, the length of the period beyond the first month can be changed to 1 month. Only 3474 s is needed for this case. Another strategy is to exclude operation modes for units according to the results of previous computation when the horizon advances or according to the experience of planners.
Our optimization model does not include all the events that may happen in a real refinery, so the detailed schedule after a short time may be useless. Then, the simulation system will be a good tool to find new schedule through what-if analysis. Simulation-based rescheduling is also an interesting approach to manage events, and we are resorting to this approach to improve our simulation system. And, the works of Adhitya. are good references for rescheduling in refineries [26, 27].
7 Conclusions
A novel short-term scheduling methodology, originally proposed by our previous research, is extended to integrate production planning and scheduling in refineries under uncertainty for plant wide management. In this article, we address the integrated scheduling/ planning model and the solution strategy. Several reasons motivate the use of a hierarchical scheduling approach for integrated planning/scheduling in refineries, one of which is the difficulty in the industrial practice to represent all the constraints in a mathematical formulation when mathematical programming is adopted. The other reason is that a monolithic mathematic model involves numerous continuous, binary variables and a large number of nonlinear constraints that may lead to the failure of getting feasible solutions at the right time. To cope with the uncertain parameters with continuous and discrete probability distribution, an integrated robust optimization is also introduced in this paper.
Nomenclature
LOM,u,m,ttotal demands forthat can’t be satisfied at the end of period, m3
INV,upenalty for inventory in tank
ONM,s,u,mflow paths that connect portof unitin operation
ONNflow paths between two units
ON,s,uflow paths that connect portof unit
OP,u,m,tpenalty for total unsatisfied demands for unitin operation
Q,s,u,mcost of raw materials
D,m,tdemand of material transferred by unitin operationin scheduling time slot, m3
M,u,m,tbinary variable denoting the end of operation modeduring period
tank farm
Atank farms
CR,u,mfraction of inflows contributing to the total charge size of unitin operation
NV,u,m,tinventory in tankin operationat the end of period, m3
PERIperimeter units that transfer crude oils into plants
S,uinflow ports of unit
Moperation modes of unit
,operation mode
TUunits with tanks excluded
PERIperimeter units that transfer products out of plants
S,uoutflow ports of unit
property
ERIperimeter units
F,u,m,tprofit for products transferred by unitin operation
LSM,u,mpenalty for unitchanging operation to
LT,upenalty for variance of charge size of unit
RO,s,u,m,p,tvalue of propertyfor the flow of portof unitin operationduring period
P,u,m,pnominal propertyfor flow of portof unitin operation
F,,m,tcharge size of unitin operationduring period, m3

Q,u,m,tvolumetric flow of portof unitin operation m during period, m3
Cscenarios
M,u,m,tbinary variable denoting the start of operation modeduring period
,port
cscenario
Aaggregate tanks in which maximum storage capacities cannot be violated
Kaggregate tanks
Ptime periods beyond the first planning period
Stime slots in the first periods
QF,u,tcharge size of unitduring period, m3
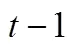
time period
processing units, perimeter units and aggregate tanks
,unit
TAaggregate tanks in which maximum storage capacities can be violated
parameter used to control trade-off between solution robustness and model robustness
IED,s,u,mstandard yield of material leaving portof unitin operation
y,m,tbinary variable denoting that unitis in operationduring period
uncertain level
parameter used to control sensitivity of the solution to the realization of uncertain data
1 Pinto, J.M., Joly, M., “Planning and scheduling models for refinery operations”,..., 24, 2259-2276 (2000).
2 Jia, Z., Ierapetritou, M., “Efficient short-term scheduling of refinery operations based on a continuous time formulation”,..., 28, 1001-1019 (2004).
3 Reddy, P.C.P., Karimi, I.A., “A new continuous-time formulation for scheduling crude oil operations”,..., 59, 1325-1341 (2004).
4 GÖthe-Lundgren, M., Lundgren, J.T., “An optimization model for refinery production scheduling”,...., 78, 255-270 (2002).
5 Glismann, K., Gruhn, G., “Short-term scheduling and recipe optimization of blending processes”,..., 25, 627-634 (2001).
6 Jia, Z., Ierapetritou, M., Kelly, J.D., “Refinery short-term scheduling using continuous time formulation: Crude-oil operations”,...., 42, 3085-3097 (2003).
7 Moro, L.F.L., Pinto, J.M., “Mixed-integer programming approach for short-term crude oil scheduling”,...., 43, 85-94 (2004).
8 Bhattacharya, S., Bose, S.K., “Mathematical model for scheduling operationsin cascaded continuous processing units”,...., 182, 1-14 (2007).
9 Pinto, J.M., Joly, M., “Planning and scheduling models for refinery operations”,..., 24, 2259 (2000).
10 Floudas, C.A., Lin, X., “Continuous-timediscrete-time approaches for scheduling of chemical processes: A review”,..., 28, 2109-2129 (2004).
11 Paolucci, M., Sacile, R., “Allocating crude oil supply to port and refinery tanks: A simulation-based decision support system”,., 33, 39-54 (2002).
12 Chryssolouris, G., Papakostas, N., “Refinery short-term scheduling with tank farm, inventory and distillation management: An integrated simulation-based approach”,...., 166, 812-827 (2005).
13 Zhao, X.Q., RONG, G., “Blending scheduling under uncertainty based on particle swarm optimization algorithm”,...., 13, 535-541 (2005).
14 Van den Heever, S.A., Grossmann, I.E., “A strategy for the integration of production planning and reactive scheduling in the optimization of a hydrogen supply network”,..., 27, 1813-1839 (2003).
15 Bassett, M.H., Dave, P., Doyle, F.J., Kudva, G.K., Pekny, J.F., Reklaitis, G.V., Subramanyam, S., Miller, D.L., Zentner, M.G., “Perspectives on model based integration of process operations”,..., 20, 821-844 (1996).
16 Birewar, D.B., Grossmann, I.E., “Simultaneous production planning and scheduling of multiproduct batch plants”,...., 29, 570 (1990).
17 Guillén, G., Badell, M., Espuna, A., Puigjaner, L., “Simultaneous optimization of process operations and financial decisions to enhance the integrated planning/scheduling of chemical supply chains”,..., 30, 421-436 (2006).
18 Cheng, L.F., Subrahmanian, E., Westerberg, A.W., “A comparison of optimal control and stochastic programming from a formulation and computation perspective”,..., 29, 149-164 (2004).
19 Sahinidis, N.V., “Optimization under uncertainty: State-of-the-art and opportunities”,..., 28, 971-983 (2004).
20 Janak, S.L., Lin, X., Floudas, C.A., “A new robust optimization approach for scheduling under uncertainty II. Uncertainty with known probability distribution”,..., 31, 171-195 (2007).
21 Leung, S.C.H., Tsang, S.O.S., Ng, W.L., Wu, Y., “A robust optimization model for multi-site production planning problem in an uncertain environment”,...., 181, 224-238 (2007).
22 Luo, C.P., Rong, G., “Hierarchical approach for short-term scheduling in refineries”,...., 46, 3656-3668 (2007).
23 Kelly, J.D., “Production modeling for multimodal operations”,, 100, 44-47 (2004).
24 Kelly, J.D., “Logistics: The missing link in blend scheduling optimization”,, 45-55 (2006).
25 Shah, N., “Mathematical programming techniques for crude oil scheduling”,..., 20, 1227-1232 (1996).
26 Adhitya, A., Srinivasan, R., Karimi, I.A., “A model-based rescheduling framework for managing abnormal supply chain events”,..., 31, 496-518 (2005).
27 Adhitya, A., Srinivasan, R., Karimi, I.A., “Heuristic rescheduling of crude oil operations to manage abnormal supply chain events”,., 53, 397-422 (2007).
Appendix A: Other constraints in the planning/ scheduling model
:

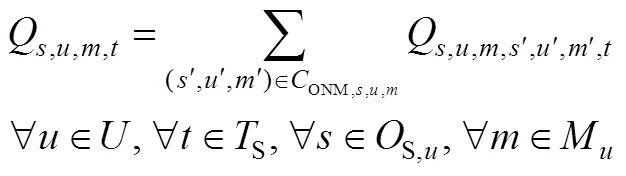

():



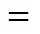
():
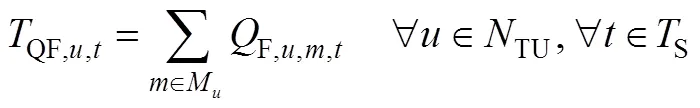

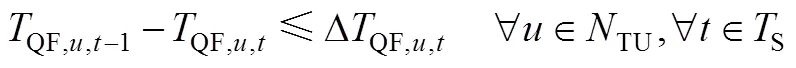

():

Yield expressions in our approach are based on a standard valueIED,,u,m, which is determined over average values obtained from plant data. In different modes of a processing unit, the materials produced have different yields.
():
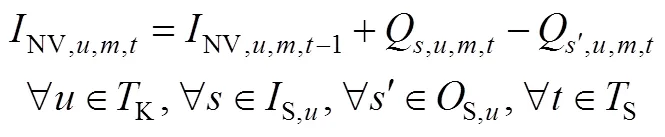
:


Whenever there is an end of the operation mode, constraint (A-11) forces the corresponding variableM,u,m,tto take the value 1. And whenever there is a start of the operation mode, constraint A-12 forces the corresponding variableM,u,m,tto be 1.
:
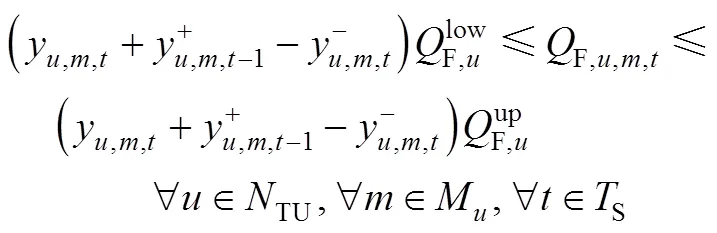
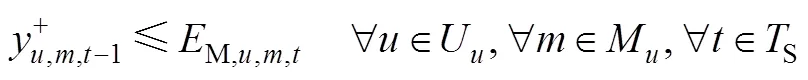

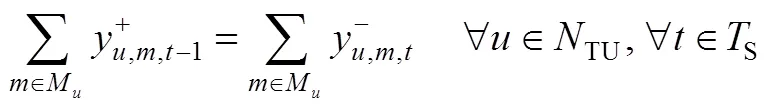
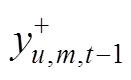
2008-05-05,
2008-08-19.
the National Natural Science Foundation of China (60421002) and the National High Technology R&D Program of China (2007AA04Z191).
** To whom correspondence should be addressed. E-mail: grong@iipc.zju.edu.cn
 Chinese Journal of Chemical Engineering2009年1期
Chinese Journal of Chemical Engineering2009年1期
- Chinese Journal of Chemical Engineering的其它文章
- Modeling and Optimization for Scheduling of Chemical Batch Processes*
- Simulation of Droplet-gas Flow in the Effervescent Atomization Spray with an Impinging Plate*
- Numerical Investigation of Constructal Distributors with Different Configurations*
- The Kinetics of the Esterification of Free Fatty Acids in Waste Cooking Oil Using Fe2(SO4)3/C Catalyst
- Multiple Model Soft Sensor Based on Affinity Propagation, Gaussian Process and Bayesian Committee Machine*
- Measurement and Correlation of Solid-Liquid Equilibria of Phenyl Salicylate with C4 Alcohols
