A Fully Flexible Potential Model for Carbon Dioxide*

ZhuAimei (朱爱梅), Zhang Xinbo (张新波), Liu Qinglin (刘庆林) and Zhang Qiugen (张秋根)



A Fully Flexible Potential Model for Carbon Dioxide*

ZhuAimei (朱爱梅), Zhang Xinbo (张新波), Liu Qinglin (刘庆林)**and Zhang Qiugen (张秋根)

National Engineering Laboratory for Green Chemical Productions of Alcohols, Ethers and Esters, Department of Chemical and Biochemical Engineering, College of Chemistry & Chemical Engineering, Xiamen University, Xiamen 361005, China

molecular simulations, radial distributions, fully flexible potential model, carbon dioxide

1 Introduction

Carbon dioxide, especially, supercritical carbon dioxide (ScCO2) is widely studied as a “green solvent” in chemical reaction and catalysis because it is nonflammable, inexpensive, nontoxic, and has exceeding miscible ability.

In order to improve the precision of physical models for solute solubility and reaction rates in a liquid and supercritical carbon dioxide, a model should include intermolecular interactions between carbon dioxide molecules and/or other solutes. For decades, the most acceptable models are fully rigid models, such as the rescaling the potential parameters of the elementary physical model (EPM2) [1], one of three different atom-atom intermolecular potentials developed by Murthy, Singer, and McDonald (MSM) [2, 3], and transferable potentials for phase equilibria (TraPPE) [4],and several optimized potential models with improvement in some aspects [5-7] have been proposed. For example, Vrabec. [5] developed the two-centers+ quadrupole model that predicted saturated vapor pressures with a better precision (10%) than the EPM2 model. Draghi. [7] added bond stretching and bending potentials and developed a fully flexible model on the basis of the EPM2 model, however, there were 11% and 15% average deviation of the saturated pressure and the saturated vapor density, respectively.

Although several potential models have been proposed for carbon dioxide, unfortunately, none of them can meet all requirements.and Car-Parrinello molecular-dynamics (CPMD) calculations on charged CO2clusters [8, 9], and neutron diffraction experiments on supercritical carbon dioxide [9-11] have shown a similar deviation. The CPMD simulations of carbon dioxide have been employed within a plane-wave- basis density functional theory (DFT). Comparing with neutron diffraction experiments, the CPMD simulations [8] on the microscopic structure of carbon dioxide are quite good, while they are unable to describe the phase behaviors accurately since they have employed only 32 molecules in the system.

The aim of this study is to find a suitable potential model for carbon dioxide, which will accurately predict both the microscopic structure and the phase behavior under high and low temperatures and pressures. For the proposed model, the ways to obtain the parameters, the methodologies, and the simulation details were provided. The simulation results of carbon dioxide obtained by the present potential and the best-known potential EPM2 were discussed, including vapor-liquid equilibra (VLE), structural properties, PVT properties, and dynamic properties.

2 Potential models

The non-bonded interactions are described by pair wise-additive Lennard-Jones (L-J) 12-6 potentials and Coulombic interactions of partial charges.

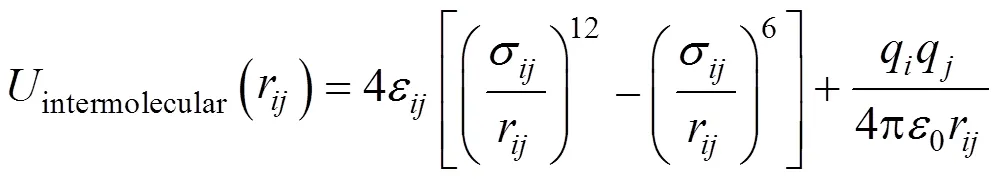
where,r,ε,σ,q,q, and0are the separation, L-J well depth, L-J size, partial charges, and permittivity of free space, respectively, for the pair of atomsand. The parameters for unlike L-J interactions are determined by Lorentz-Berthelot combining rules [13].

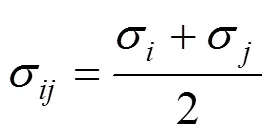
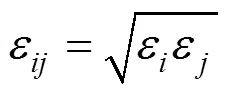
The long-range interactions using a Group based summation method [14-16] were compared with the Ewald summation. The intramolecular part consists of harmonic bond stretching and bond angle vibration terms in the equation below

where,,0,, and0are the measured bending length, the equilibrium bending length, the measured bending angle, and the equilibrium bending angle, respectively; andkandkare the force constants.

The force field parameters are obtained using the optimization method proposed by Zhang [6] and Khare. [16]. Firstly, we understand how the parameters affect the simulations results. The initial force constants are obtained from quantum chemical calculations, and the other initial parameters are obtained from the EPM2 model. For example, the PVT properties at supercritical conditions for carbon dioxide are calculated to get a prerequisite knowledge of the parameter spaces. Then, the Lennard-Jones parameters of oxygen or carbon atom are changed, and the PVT properties of carbon dioxide that are the most sensitive to the Lennard-Jones parameter of oxygen atoms are slightly changed to get good results. The analysis of the carbon dioxide structure shows that the equilibrium bending length is short, which is consequently increased. The process described above was repeated to obtain all the optimized parameters that were different from the initial parameters. All the parameters for carbon dioxide in this study are listed in Table 1.

3 Simulation Details

3.1 Phase equilibrium simulations

Pure component vapor-liquid equilibria were obtained using the NVT-Gibbs ensemble Monte Carlo (GEMC) method [17] with periodic boundary conditions. The intra and intermolecular force field parameters adopted are shown in Table 1. The simulation system contained 400-500 molecules. Simulations for the vapor-liquid equilibria at high temperature consisted of 1.2´107moves, and longer simulations (1.5´107) were required at low temperatures. The ratio of the different types of Monte Carlo moves was 13%-16% translation moves, 13%-16% rotation moves, 8%-12% volume moves, and the rest were transfer moves that were employed. The temperature increases with the decreasing of the ratio of transfer moves. A cutoff distance of 1.05 nm was used for the non-bonded interactions, with long-range corrections applied beyond this distance for the van der Waals interactions. Initial configurations were based on the face centered cubic (fcc) lattice. Then, enough Monte Carlo cycles (1×104moves) at an elevated temperature were used to “melt” the crystal structure, and the system was then “cooled” to the desired temperature.

Owing to the large fluctuations near the critical point, it is not possible to determine its location explicitly. Simulation data at subcritical conditions are used to estimate the critical point by invoking the following scaling law

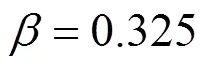
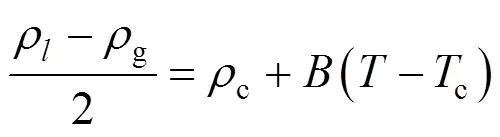
where,is a constant, andcis the critical density. The critical pressures were found by extrapolating the vapor pressure curve to the critical temperature. The vapor pressures were fitted to the semi-empirical equation [18]

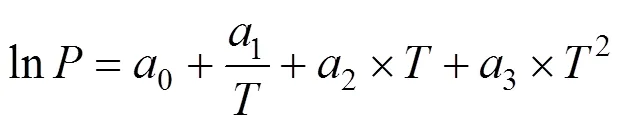
where,0-3are the fitting constants.

3.2 Pressure, self-diffusion coefficient, and structure of pure carbon dioxide

In our molecular dynamics simulations, 400 molecules were placed in a cubic simulation box. The conventional periodic boundary conditions and minimum image conventions were used in the simulations. Velocity Verlet algorithm was adopted to propagate the statistical trajectory. Long-range electrostatic forces and energies were calculatedthe group based method, which was compared with the Ewald method in calculating the pressures of VLE. The constant number of atom, pressure and temperature ensemble molecular dynamics (NPT-MD) simulations proposed by Khare. [14-16] were used to calculate the vapor pressures (the saturated pressures), and then the pressure-density data were fitted linearly to determine the vapor pressure corresponding to the equilibrium vapor density from coexisting calculations. The NPT-MD ensemble was also used to calculate the dynamic properties, and the self-diffusion coefficients were calculated by the Einstein equation [19]:

where,r() is the molecular positionat time, and ther(0) is the initial position.

The constant number of atom, volume and temperature ensemble molecular dynamics (NVT-MD) ensemble was used to investigate the structural properties of pure carbon dioxide. All the simulations were run at the time step of 1 fs for 120 ps, using the method of Andersen and Berendsen for the temperature control and the pressure control, respectively. The choice of the simulation length, number of molecules,., in this study is made on the basis of Ref. [14-16].

Table 1 Parameters for carbon dioxide in this study

4 Results and Discussion

Figure 1 shows the simulated coexistence envelopes, the experimental observations [20], and the literature simulation data [5, 21]. At 230 K, the deviations of the saturated liquid and vapor density are 0.5% and 17% (EPM2), and 0.2% and 18% (TraPPE), respectively. At 290 K, the maximums are 3.3% and 8.7% (EPM2), and 3.5% and 18.6% (TraPPE), respectively. The present model shows as good results as the EPM2 and TraPPE models below 260 K. The deviations of the saturated liquid and vapor density by the present model are 0.6% and 1.3% (230 K), and 0.7% and 2.0% (290 K), respectively. The average absolute deviation by the EPM2, TraPPE, and the present model are 2.3% and 6.3%, 1.7% and 19.1%, and 0.3% and 2.0%, respectively. Generally, the present model produces improved saturated liquid and vapor density over the two well-known models in a wide temperature range, especially at higher temperatures.

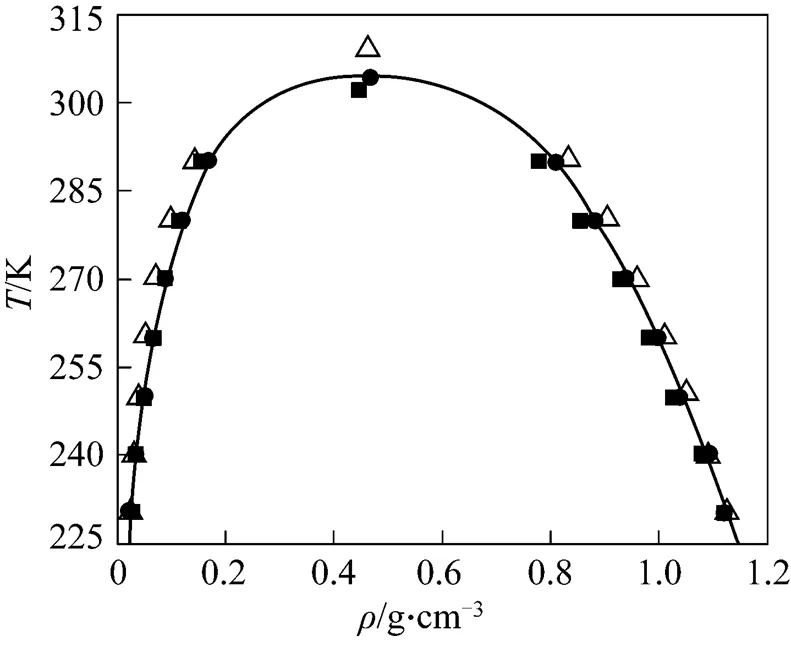
Figure 1 Pure carbon dioxide phase equilibria—— Exp. [20];△ TraPPE [6];■ EPM2 [21];● this work

The experimental data [20], the literature simulation data [1, 4, 6], and the predictions in this study for the critical properties are shown in Table 2. The EPM2 predictions agree with the experimental data for the critical density and pressure, however, there is significant deviation for the critical temperature. The critical pressure predicted by the MSM and TraPPE models is either considerably lower or higher than the experimental data. The critical properties obtained by the Errington and the present model agree with the experimental values. In this study, the deviation ofc,c, andcare only 0.09 K, 0.0003 g×cm－3, and 0.01 MPa, respectively.

Table 2 Critical properties of carbon dioxide reproduced by different models

The simulated densities by the present model and the experimental data [20] from 5 to 800 MPa are shownin Fig. 2. The relative errors for other models increased almost parallel with increasing the pressures [5]. The largest deviation for the EPM2 model is almost 7 % at 980.65 K and 800 MPa. Below 100 MPa, the simulated densities of the present model agree with the experimental data. In the range of 100 to 800 MPa, the deviations increase slightly, and the largest deviation is 5 % at 1100 K and 800 MPa.

Figure 3 Snapshot of CO2under the supercritical state from the NVT-MD simulations (Oxygen atoms are in white, and carbon atoms are in gray)

Table 3 The structural features for ScCO2

The self-diffusion coefficient estimated by the present model and the experimental observations [22] are shown in Table 4. The self-diffusion coefficient at supercritical condition is important for chemical industries, particularly at 10-15 MPa. The best prediction of the present model is at 13.79 MPa and the predicted results are also reasonable with increasing the pressures in the supercritical condition.

Table 4 Self-diffusion coefficients estimated by this study and the experiments at 348.15 K

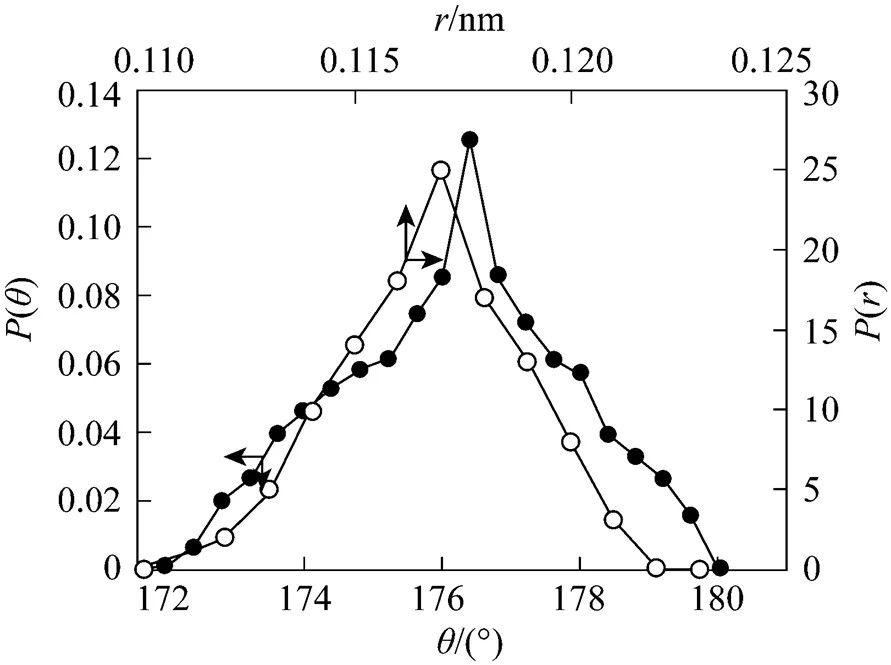
5 Conclusions

A new fully flexible potential model for carbon dioxide was optimized to reproduce experimental properties. The phase equilibrium of pure carbon dioxide was calculated by the GEMC over a wide temperature range. The densities of supercritical carbon dioxide and the structural properties (318.15 K and 0.703 g×cm－3) for carbon dioxide were calculated using the present method. Radial distribution functions for ScCO2were calculated. The critical properties were estimated from subcritical simulation data using the critical scaling laws.

1 Harris, J.G., Yung, K.H., “Carbon dioxide’s liquid-vapor coexistence curve and critical properties as predicted by a simple molecular model”,..., 99, 12021-12024 (1995).

2 Murthy, C.S., Oshea, S.F., McDonald, I.R., “Electrostatic interactions in molecular crystals: lattice dynamics of solid nitrogen and carbon dioxide”,.., 50, 531-541 (1983).

3 Geiger, L.C., Ladanyi, B.M., Chapin, M.E., “A comparison of models for depolarized light scattering in supercritical CO2”,..., 93, 4533-4542 (1990).

4 Potoff, J.J., Siepmann, J.I., “Vapor-liquid equilibria of mixtures containing alkanes, carbon dioxide, and nitrogen”,., 47, 1676-1682 (2001).

5 Vrabec, J., Stoll, J., Hasse, H., “A set of molecular models for symmetric quadrupolar fluids”,..., 105, 12126-12133 (2001).

6 Zhang, Z., Duan, Z., “An optimized molecular potential for carbon dioxide”,..., 122, 214507-214522 (2005).

7 Draghi, C.N., Bruin, T.D., Pellitero, J.P., Avalos, J.B., Mackie, A.D., “Thermodynamic and transport properties of carbon dioxide from molecular simulation”,..., 126, 064509-1-8 (2007).

8 Saharay, M., Balasubramanian, S., “molecular-dynamics study of supercritical carbon dioxide”,..., 120, 9694-9702 (2004).

9 Zhang, Y., Yang, J., Yu, Y., “Dielectric constant and density dependence of the structure of supercritical carbon dioxide using a new modified empirical potential model: A Monte Carlo simulation study”,..., 109, 13375-13382 (2005).

10 Ishii, R., Okazaki, S., Odawara, O., Okada, I., Misawa, M., Fukunaga, T., “Structural study of supercritical carbon dioxide by neutron diffraction”,., 104, 291-304 (1995).

11 Ishii, R., Okazaki, S., Okada, I., Furusaka, M., Watanabe, N., Misawa, M., Fukunaga, T., “Density dependence of structure of supercritical carbon dioxide along an isotherm”,..., 105, 7011-7021 (1996).

12 Fedchenia, I.I., Schröder, J., “Local orientational correlations and short time anisotropic motion in molecular liquids: computer simulations of liquid CO2”,..., 106, 7749-7755 (1997).

13 Kolafa, J., Nezbeda, I., Lisal, M., “Effect of short- and long-range forces on the properties of fluids. III. Dipolar and quadrupolar fluids”,.., 99, 1751-1764 (2001).

14 Chen, B., Potoff, J.J., Siepmann, J.I., “Monte Carlo calculations for alcohol and their mixtures with alkanes. Transferable potential for phase equilibra.5.united-atom description of primary, secondary, and tertiary alcohols”,..., 105, 3093-3104 (2001).

15 Nath, S.K., “Molecular simulation of vapor-liquid phase equilibria of hydrogen sulfide and its mixtures with alkanes”,..., 107, 9498-9504 (2003).

16 Khare, R., Sum, A.K., Nath, S.K., de Pablo, J.J., “Simulation of vapor-liquid phase equilibria of primary alcohols and alcohol-alkane mixtures”,..., 108, 10071-10076 (2004).

17 de Pablo, J.J., Laso, M., Suter, U.W., “Simulation of polyethylene above and below the melting point”,..., 96, 6157-6162 (1992).

18 Errington, J.R., Panagiotopoulos, A.Z., “Phase equilibria of the modified Buckingham exponential-6 potential from Hamiltonian scaling grand canonical Monte Carlo”,..., 109, 1093-1100 (1998).

19 Allen, M.P., Tildesley, D.J., Computer Simulation of Liquids, Oxford Science, Oxford (1989).

20 National Institute of Standards and Technology, NIST Chemistry WebBook, http://webbook.nist.gov/chemistry

21 Vorholz, J., Harismiadis, V.I., Rumpf, B., Panagiotopoulos, A.Z., Maurer, G., “Vapor plus liquid equilibrium of water, carbon dioxide, and the binary system, water plus carbon dioxide, from molecular simulation”,, 170, 203-234 (2000).

22 Etesse, P., Zega, J.A., Kobayashi, R., “High pressure nuclear magnetic resonance measurement of spin-lattice relaxation and self-diffusion in carbon dioxide”,..., 97, 2022-2029 (1992).

2008-07-30,

2008-12-01.

the National Natural Science Foundation of China (50573063), the Program for New Century Excellent Talents in University of the State Ministry of Education (NCET-05-0566) and the Specialized Research Fund for the Doctoral Program of Higher Education of China (2005038401).

** To whom correspondence should be addressed. E-mail: qlliu@xmu.edu.cn