Activity Coefficient Models to Describe Vapor-Liquid Equilibrium in Ternary Hydro-Alcoholic Solutions*
Claudio A. Faúndezand José O. Valderrama
Activity Coefficient Models to Describe Vapor-Liquid Equilibrium in Ternary Hydro-Alcoholic Solutions*
Claudio A. Faúndez1and José O. Valderrama2,3,**
1Universidad de Concepción, Fac. de Cs. Físicas y Matemáticas, Casilla 160-C, Concepción, Chile2Universidad de La Serena, Fac. de Ingeniería, Casilla 554, La Serena, Chile3Centro de Información Tecnológica (CIT), Casilla 724, La Serena, Chile
In this study, three semipredictive activity coefficient models: Wilson, non-random-two liquid model (NRTL), and universal quasi-chemical model (UNIQUAC), have been used for modeling vapor-liquid equilibrium properties of ternary mixtures that include substances found in alcoholic distillation processes of wine and musts. In particular, vapor-liquid equilibrium in ternary mixtures containing water + ethanol + congener has been modeled using parameters obtained from binary and ternary mixture data. The congeners are substances that although present in very low concentrations, of the order of part per million, are important enological parameters. The results given by these different models have been compared with literature data and conclusions about the accuracy of the models studied are drawn, recommending the best models for correlating and predicting phase equilibrium properties of this type of mixtures.
wine distillation, activity coefficient models, vapor-liquid equilibrium
1 Introduction
To design and simulate alcoholic distillation processes, knowledge of the equilibrium conditions is of special importance. This is because the driving force that produces component separation is the difference between the actual concentration and the concentration at thermodynamic equilibrium. Therefore, knowledge of vapor-liquid equilibrium conditions (VLE) is necessary to design and optimize distillation processes. In wine and must distillation, the great amount of substances found in the mixture to be distilled and the very low concentration of several other components (different from ethanol and water), called congeners, makes it difficult to correlate and predict the concentration of the distilled product, considered to be the most important variable in the produced spirit[1, 2]. Several congener compounds form an essential part of the aroma of the distilled product and therefore their concentrations are important enological parameters [3]. These congener substances are usually present in concentrations of part per million, 10-6to 10-4mg·L-1[4, 5].
As known, the phase equilibrium problem to be solved consists of the calculation of some variables of the set,,,(temperature, pressure, liquid-phase concentration, and vapor-phase concentration, respectively), when some of them are known. For a vapor- liquid mixture in thermodynamic equilibrium, the temperature and the pressure are the same in both phases, and the remaining variables are defined by the material balance and the “fundamental equation of phase equilibrium”. The application of this fundamental equation requires the use of thermodynamic models, which normally include binary interaction parameters.
The operating pressure in most alcoholic distillation processes is of the order of the atmospheric pressure and most of the substances involved are highly polar. The classical thermodynamic models commonly used in the literature to treat these mixtures at low pressure require a great amount of binary parameters, which must be determined from binary experimental data [6]. Theoretically, once these binary parameters are known, one can predict the behavior of multicomponent mixtures using standard thermodynamic relations and thermodynamics models.
Binary mixtures containing water + congeners and ethanol + congeners have been studied in literature [7-10] and values of the binary parameters have been provided for several models. However, the use of binary parameters to treat mixtures with more than two components in wine distillation process has not been thoroughly analyzed. The authors have analyzed selected ternary mixtures water + congener + congener and ethanol + congener + congener [11], however, the strong interaction between ethanol and water in ternary mixtures was not analyzed. This article considers the study of twelve ternary mixtures containing water+ ethanol + congener. The twelve congeners are: acetaldehyde, ethyl acetate, furfural, methanol, 3-methyl-1-butanol, 2-methyl-1-propanol, 1-pentanol, 1-propanol, 2-propanol, methyl acetate, 1-butanol, and butyl acetate. The first 8 congeners mentioned are considered as legal compounds by the Chilean legislation for the production of a spirit called “Pisco” and are controlled by the Chilean Health Ministry. As stated above, in wine distillation process, the congeners are present in low concentrations and modeling studies should consider this aspect. However, the limited experimental data available in open literature place an additional difficulty to more accurately correlate these mixtures in the congener infinite dilution region. Therefore in these cases where data is not available in the low concentration range for the congeners, we rely on the extrapolation capabilities of the models used.
The fundamental equations of phase equilibrium are described as follows.
Equality of fugacities of each component in the mixture in both phases:
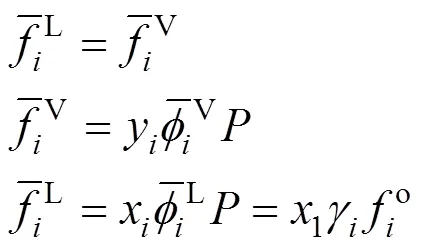
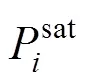
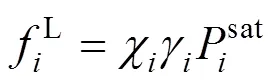
The fugacity is related to the temperature, the pressure, the volume, and the concentration through a standard thermodynamic relation [12]. If the fugacity coefficient is used in both phases, the method of solution of the phase equilibrium problem is known as “the equation of state method”. If the fugacity coefficient is used for the vapor phase and the activity coefficient is used for the liquid phase, the equilibrium problem is known as “the gamma-phi method”. If the equation of state method is used, an equation of state and a set of mixing rules are needed, to express the fugacity coefficient as a function of the temperature, the pressure, and the concentration. Modern equation of state methods include an excess Gibbs free energy model (E) in the mixing rules of the equation of state, giving origin to the so-called “equation of state +Emodel” [13].
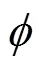
Most models available in literature for the activity coefficient are of the correlating type (Van Laar, Margules, Redlich-Kister, NRTL, UNIQUAC, and Wilson), indicating that experimental data are needed to calculate certain empirical parameters; although some predictive models are also available [universal functional activity coefficient model (UNIFAC), analytical solution of groups (ASOG)]. An interesting model to explore for predicting VLE in mixtures of interest in wine distillation is the predictive Soave- Redlich-Kwong (PSRK) of the group “equation of state +Emodel”, proposed by Holderbaum and Gmehling [15]. This predictive model has been used in several applications including mixtures containing ethanol, water, and congeners [16]. However, to the best of the authors’s knowledge, no systematic study on ternary mixtures, as the one presented here, has been published.
In the study detailed in this article, ternary mixtures congener + ethanol + water were considered. Three activity coefficient models, Wilson, non-random-two liquid model (NRTL), and universal quasi-chemical model (UNIQUAC), are analyzed and the result compared with experimental data available in literature. Two approaches are considered: i) ternary data are predicted using parameters obtained from binary VLE data only; and ii) ternary data are correlated using the ternary VLE data. In both cases, it is assumed in the modeling that the model parameters are independent on concentration and temperature. The first approach makes use of the so-called pair wise additivity concept. This indicates that the pair interactions coefficients do not depend on the presence of other components in the mixture, therefore, interaction between molecules 1 and 2, for instance, are the same in a ternary or multicomponent mixture in which the components 1 and 2 are present. The second approach represents a simple correlation procedure in which the binary interaction parameters,Afor Wilson,Bandαfor NRTL, andUfor UNIQUAC, are calculated using ternary VLE data.
2 Model Description
The main equations for the three models studied (Wilson, NRTL, and UNIQUAC) and the meaning of the different variables and parameters are described in the following.


2.1 Wilson model
Wilson (1964) [18] presented the following expression for the liquid phase activity coefficients:
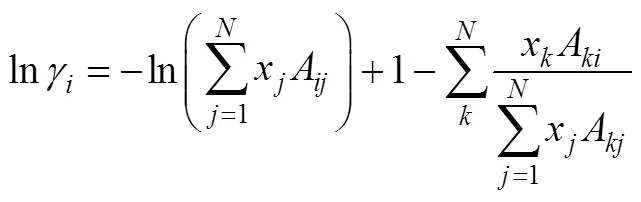
The details of the Wilson model are given below.
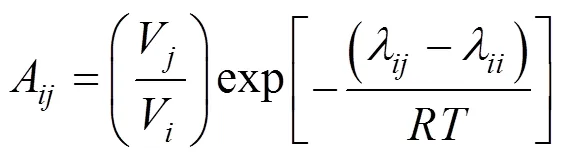
whereV, liquid molar volume of component;,empirical energy term;x, mole fraction of component.
UNIQUAC model
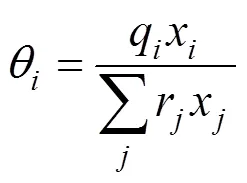
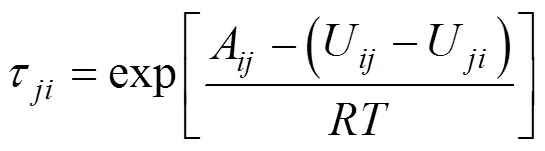

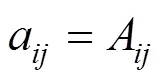
2.2 NRTL model
The NRTL model for the activity coefficient at a given absolute temperaturein Kelvin has the following form [19]:
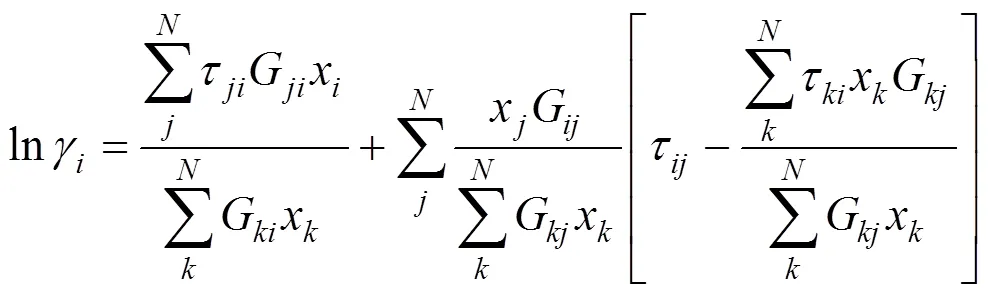
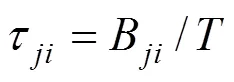
The termsB,B, andrepresent adjustable parameters usually calculated from the experimental vapor- liquid equilibrium data.
2.3 UNIQUAC model
The Universal Quasi-Chemical theory, from which the UNIQUAC model is derived, can be expressed in terms of the activity coefficients as Ref. [20]:

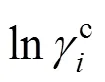
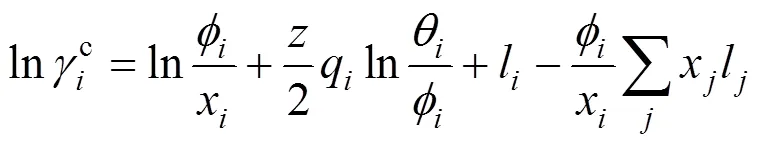
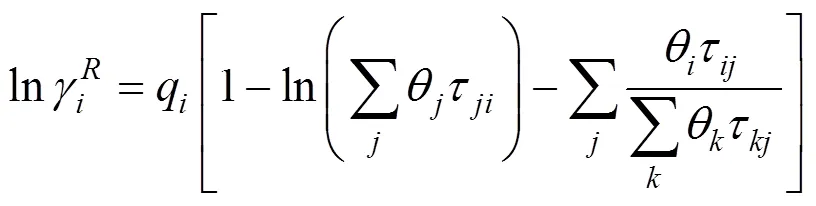
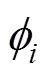
3 Ternary mixtures
Twelve ternary ethanol + water + congener mixtures were considered for the study. The congeners included in these mixtures are acetaldehyde, ethyl acetate, furfural, methanol, 3-methyl-1-butanol, 2-methyl-1-propanol, 1-pentanol, 1-propanol, 2-propanol, methyl acetate, 1-butanol, and butyl acetate.
Table 1 shows some pure component properties for all the substances involved in this study. In the table,Wis the molecular weight,bis the normal boiling temperature,cis the critical temperature,cis the critical pressure,cis the critical volume, andis the acentric factor. The data were obtained from Refs. [21, 22].
教学中要以紧扣教学重点为基础,精选关键问题,改变重点不突出、满堂问的毛病,调动学生学习的积极性,以读为主,有足够思考的空间,进行创造性学习。一堂课的教学不能离开主线、重点,否则支离破碎,达不到效果,教学目标难以达成。
Table 2 provides some details on the experimental data used in the study. In this table, Δis the temperature range (in K) in the data set, Δxis the liquid mole fraction range for the component “”, and Δyis the vapor mole fraction range for the component “”. The experimental data used in the study were obtained from Refs. [6, 22-24], as detailed in Table 2.
Although values of the interaction parameters in the Wilson, NRTL, and UNIQUAC models [Eq. (4) for Wilson, Eq. (7) for NRTL, and Eq. (5) for UNIQUAC], are given in literature for most binary pairs, in this study, these parameters were obtained from available experimental binary and ternary VLE data. This was done because the range of temperature and pressure for the data presented in the literature are not necessarily the same as for the data used in this study. This is the recommended way to analyze these types of systems if better results are desired [7]. The new binary and ternary mixture parameters are shown in Table 3 for the three models.
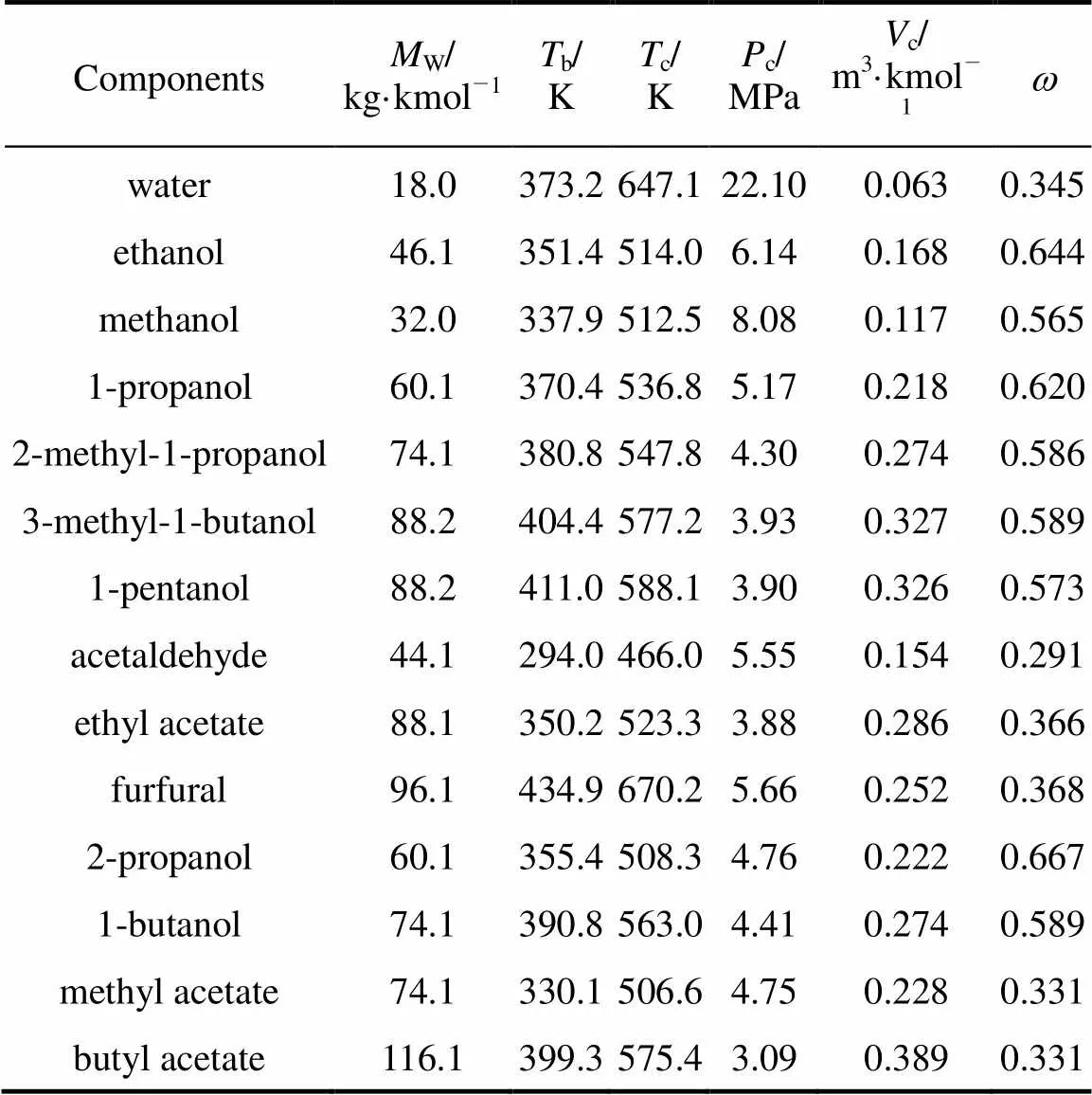
Table 1 Some properties for the substances involved in this study
According to the Phase Rule for a three-component mixture, three variables must be set to calculate the rest[12]. Here, pressure () and concentration of water in both phases (3and3) are given, while the temperature () and concentration of the other components (1,1,2and2) are calculated, thereby determining the optimum binary parameters .
4 Results and Discussion
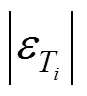
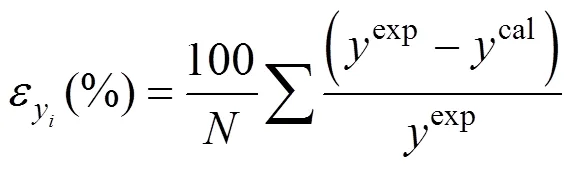
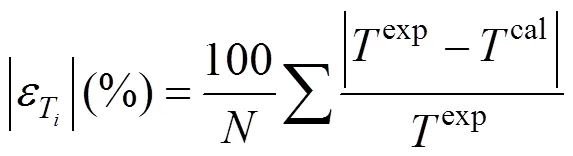
In these tables, the deviations for water concentration3are not shown since the water concentrations in both phases are the data given in the bubble temperature calculations. Since for wine distillation, the congener concentration is of more interest, the results and discussion refer to this variable. The temperature is generally well predicted by all models; however, it is better when the model parameters (given in Table 3) are obtained from ternary data. Table 4, also shows the deviations calculated using the activity coefficient models Wilson, NRTL, and UNIQUAC with parameter obtained from VLE binary and ternary data.

Table 2 Temperature and mole fraction ranges for the experimental data employed in the analysis
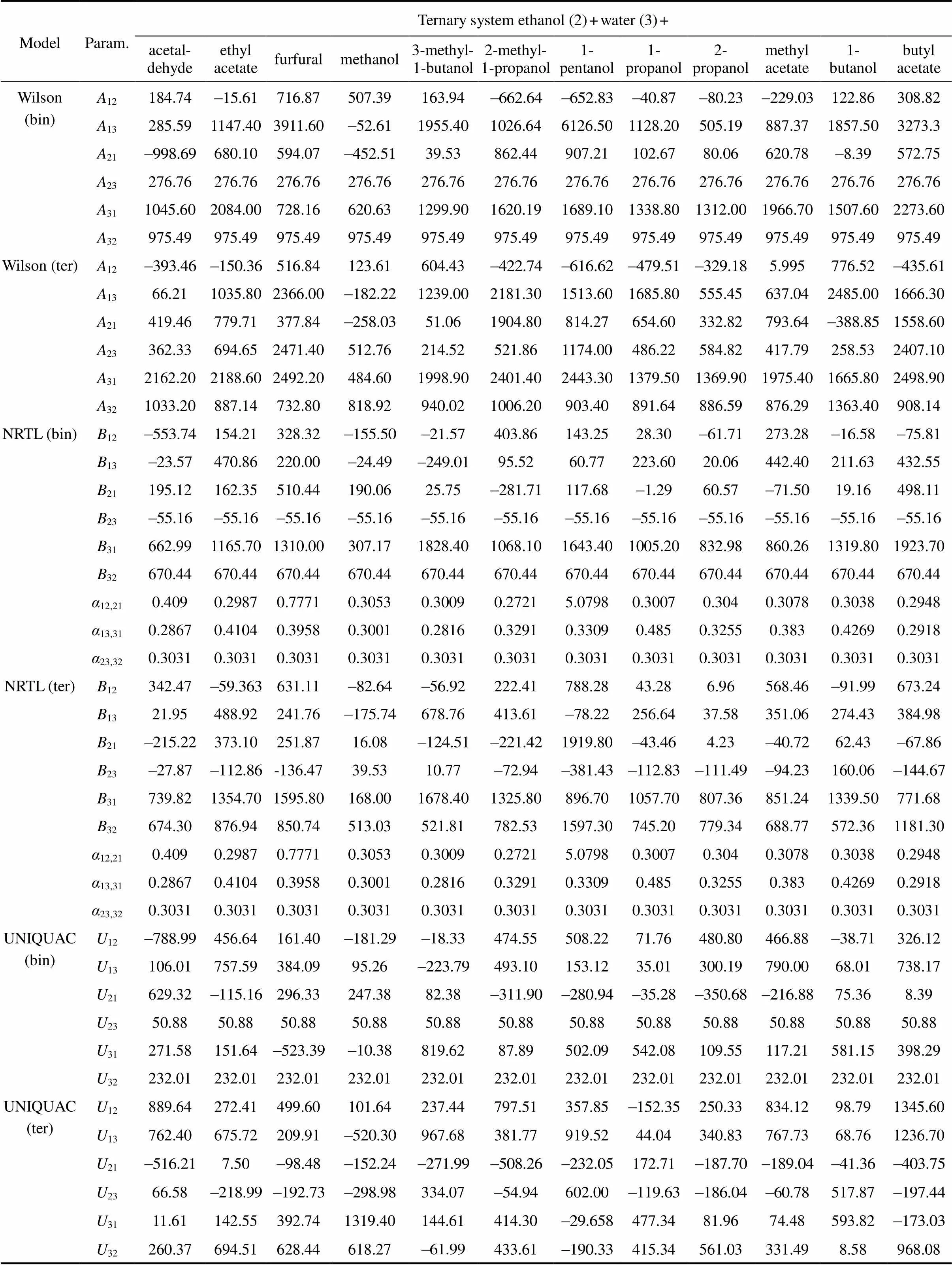
Table 3 Parameters (Aij, Bij, Uij and αij) for the models Wilson, NRTL and UNIQUAC calculated from experimental binary (bin) and ternary (ter) VLE data
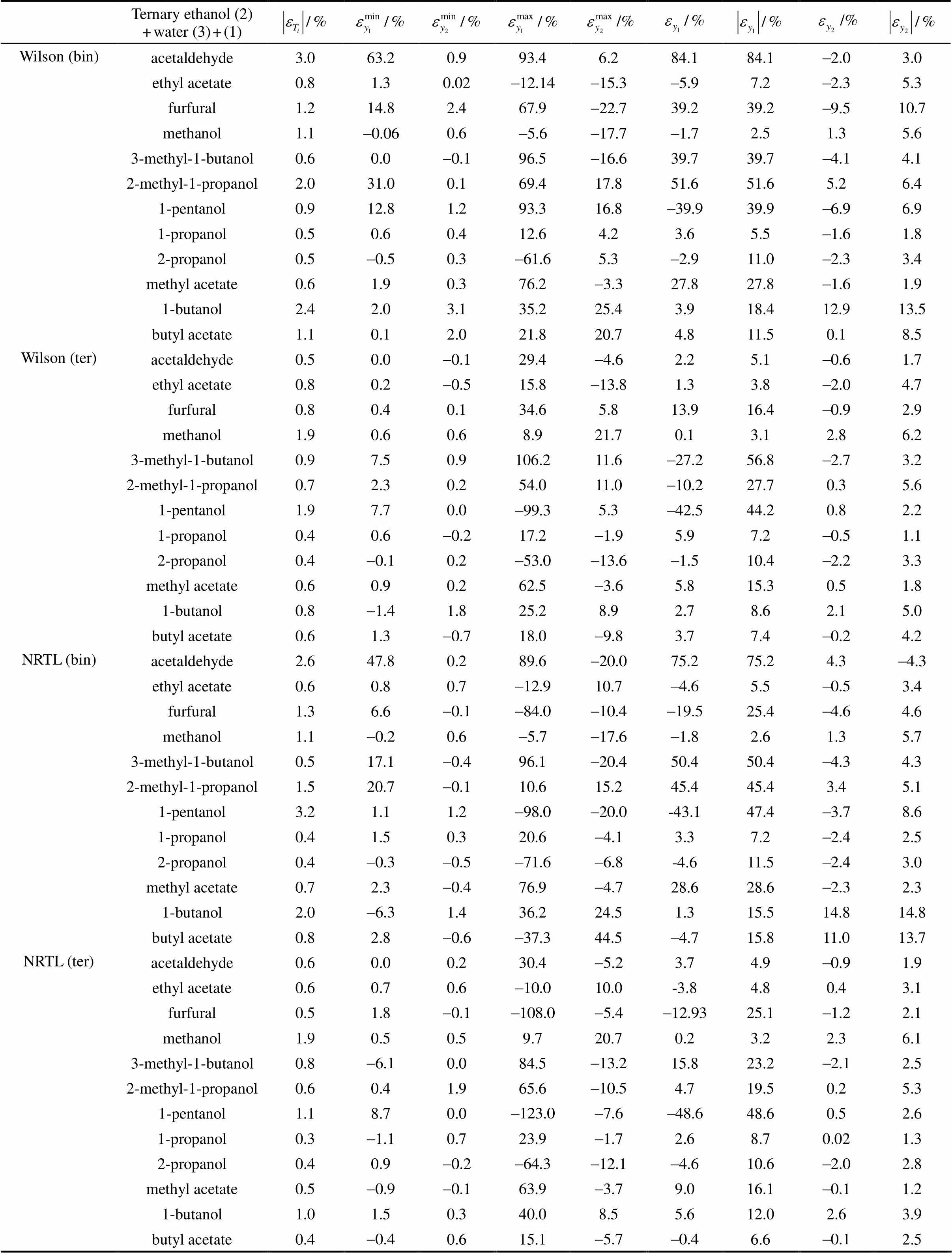
Table 4 Minimum, maximum, and average deviations for the vapor phase mole fraction of components (1) and (2) for the ternary system: congener (1) + ethanol (2) + water (3), using binary and ternary parameters with the models Wilson,NRTL and UNIQUAC
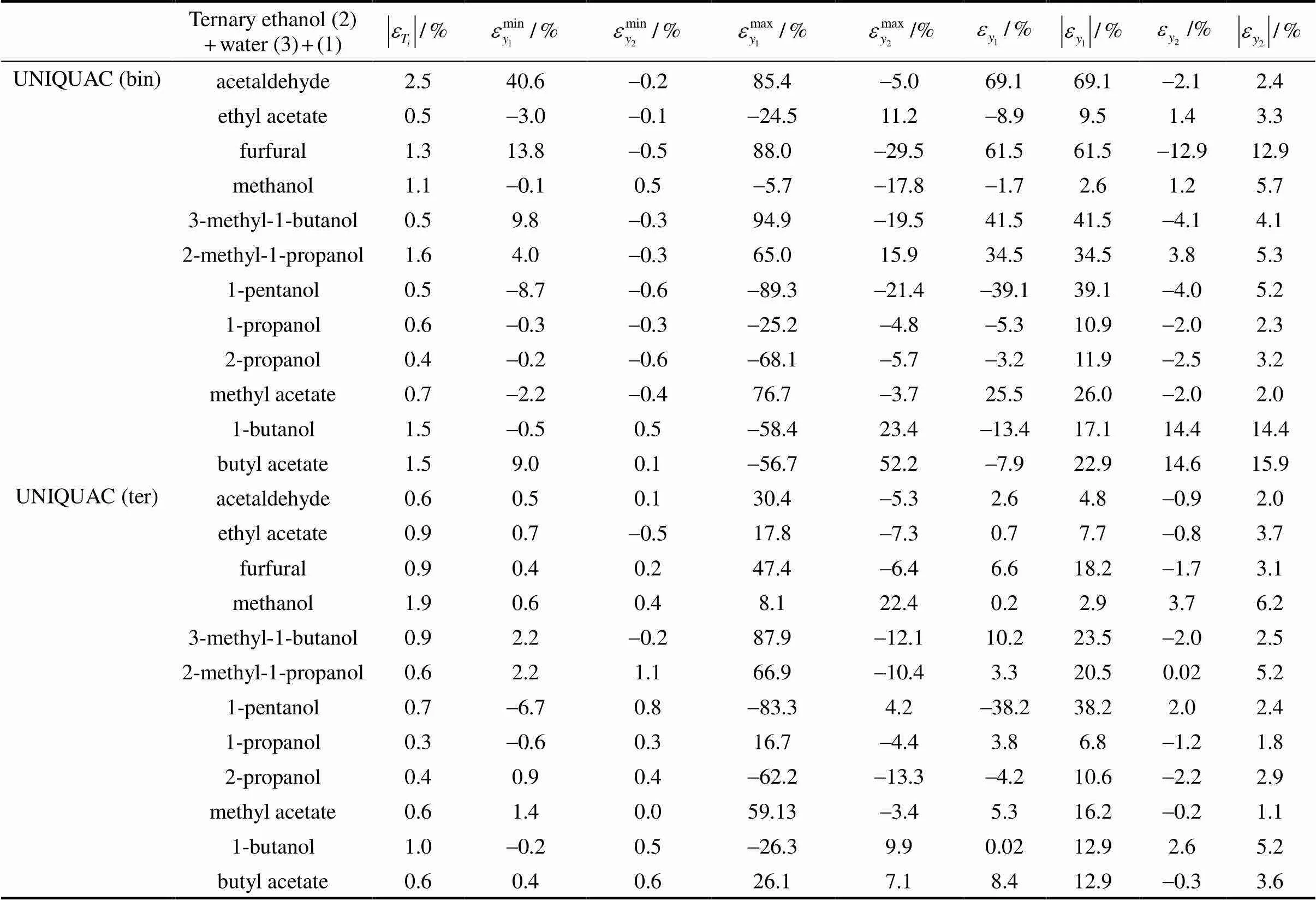
Table 4 (Continued)
As observed in the Table, the Wilson model with parameters obtained from VLE data of binary systems, predicts concentration (1) with relative and absolute deviations below 30% for only seven of the twelve systems analyzed. The highest absolute deviations, between 39% and 85%, are found for the mixtures acetaldehyde (1) + ethanol (2) + water (3), furfural (1) + ethanol (2) + water (3), 3-methyl-1-butanol (1) + ethanol (2) + water (3), 2-methyl-1-propanol (1) + ethanol (2) + water (3) and 1-pentanol (1) + ethanol (2) + water (3). These models provide lower deviations for the ethanol concentration in the gas phase (below 14%).
When the Wilson model is used with parameters obtained from VLE data of ternary systems, the concentration values1present relative and absolute deviations below 30% for ten of the twelve systems analyzed. The highest absolute deviations, between 44% and 57%, are found for the mixtures 3-methyl-1- butanol (1) + ethanol (2) + water (3) and 1-pentanol (1) + ethanol (2) + water (3). Wilson model gives lower deviations for the ethanol concentration in the gas phase (below 7%).
The NRTL model used with parameters obtained from VLE data of binary systems, predicts the concentration1with relative and absolute deviations below 30% for eight of the twelve systems analyzed. The highest absolute deviations, between 45% and 76%, are found for the mixtures acetaldehyde (1) + ethanol (2) + water (3), 3-methyl-1-butanol (1) + ethanol (2) + water (3), 2-methyl-1-propanol (1) + ethanol (2) + water (3) and 1-pentanol (1) + ethanol (2) + water (3). When NRTL model is used with parameters obtained from VLE data of ternary systems, it predicts concentration1with relative and absolute deviations below 30% for eleven of the twelve systems analyzed. The high absolute deviation, of 45% is found for the mixtures 1-pentanol (1) + ethanol (2) + water (3).
The UNIQUAC model used with parameters obtained from VLE data of binary systems, predicts the concentration1with relative and absolute deviations below 30% for seven of the twelve systems analyzed. The highest absolute deviations, between 34% and 70%, are found for the mixtures acetaldehyde (1) + ethanol (2) + water (3), furfural (1) + ethanol (2) + water (3), 3-methyl-1-butanol (1) + ethanol (2) + water (3), 2-methyl-1-propanol (1) + ethanol (2) + water (3) and 1-pentanol (1) + ethanol (2) + water (3).
Now, if we use the UNIQUAC model with parameters obtained from VLE data of ternary systems, this model predicts the concentration1with relative and absolute deviations below 30% for eleven of the twelve systems analyzed. For the mixture 1-pentanol (1) + ethanol (2) + water (3), the high absolute deviation (38%) is found. In all the cases analyzed and discussed above, the ethanol concentration in the gas phase is obtained with relative low deviations (below 15% for the predictive models and below 7% for the correlating models).
As seen in Table 4, Wilson, NRTL, and UNIQUAC models give better results when the parameters obtained from experimental data of ternary systems are used, as expected. Although, theoretically, the use of parameters obtained from binary mixture data can be used to predict VLE in ternary mixtures containing the binary mixture substances, however, this is not true in practice. This fact indicates the inaccuracy of the approach and the limitations of the model to capture these inaccuracies. For example, in the system acetaldehyde (1) + ethanol (2) + water (3), prediction of concentration1is considerably improved when the three models are used with parameters obtained from ternary data. This is also true for the prediction of concentration of ethanol in the gas phase2in which deviations are lower. Similarly, better results of2are obtained for the system 1-butanol (1) + ethanol (2) + water (3). On the whole, the NRTL and the UNIQUAC models give similar deviations.
In Figs. 2 and 3, the results obtained with parameters calculated from ternary data are shown, for the three models. Fig. 2 shows the individual relative deviations of the predicted congener concentration in the gas phase1in the mixture 3-methyl-1-butanol (1) + ethanol (2) + water (3). Experimental data are taken from Hausen [23] and the calculated values are obtained from the models NRTL, UNIQUAC, and Wilson. As observed in the figure, to lower concentrations of1, the Wilson model gives higher individual relative deviations. The three models did not satisfactorily reproduce the highest concentration of1. In this case, individual relative deviations are about 90%. For this system, the models NRTL and UNIQUAC give similar deviations.
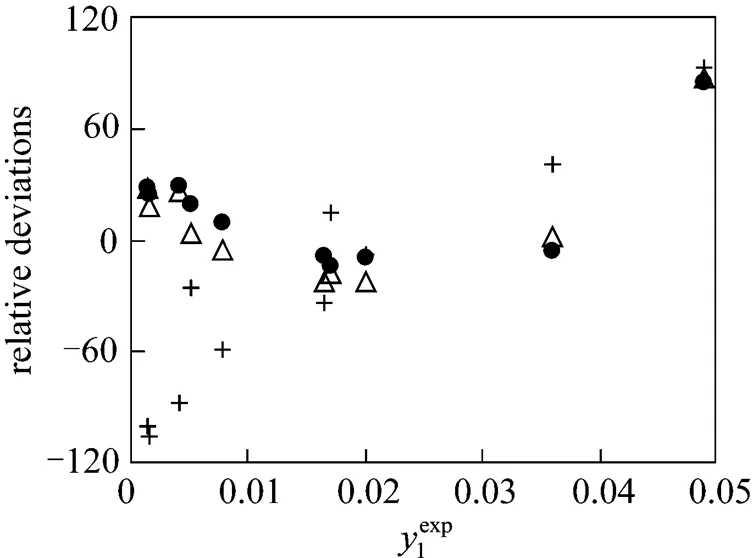
Figure 2 Individual relative deviations of the predicted congener concentration in the gas phase (1) in the mixture 3-methyl-1-butanol (1) + ethanol (2) + water (3)
● NRTL;△ UNIQUAC; + Wilson
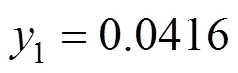
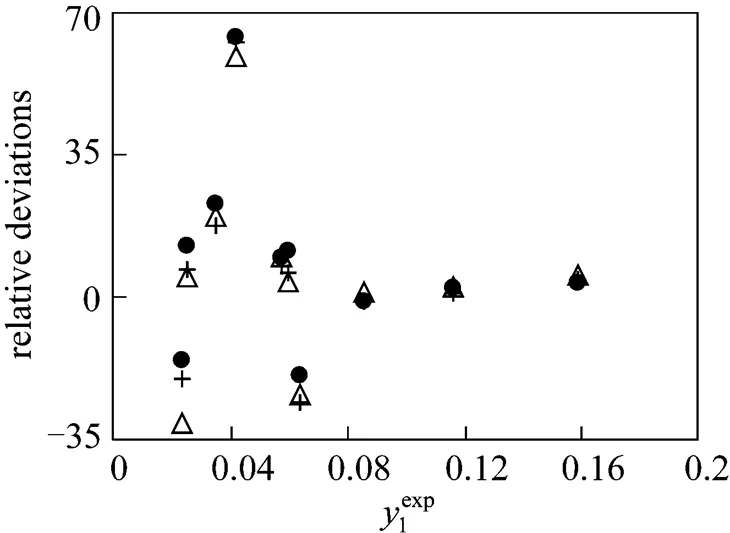
Figure 3 Individual relative deviations of the predicted congener concentration in the gas phase (1) in the mixture methyl acetate (1) + ethanol (2) + water (3)
● NRTL;△ UNIQUAC; + Wilson
Although one model gives better results for some particular cases, it is not possible to generalize the results and select one of the models used as the best one for this type of complex mixtures that appear in wine distillation processes. If better results are desired, further studies are needed with data restricted to narrower ranges of temperature, pressure, and concentration. Also, more complex models, hopefully specific for hydro-alcoholic mixtures, should be used.
It should be finally mentioned that although there are numerous data on compositions of wine distillates [25-27], the information provided is not given in the required form for the type of modeling needed in alcoholic distillation processes. In the Dechema Database [6], the only multicomponent mixture ethanol + water + congeners is the five-component mixture water + ethanol + methyl acetate + ethyl acetate +-propanol. This mixture includes congeners of interest in other distillation processes but not in the production of “Pisco”.
5 Conclusions
Vapor-liquid equilibrium in ternary mixtures containing water + ethanol + congener has been modeled using parameters obtained from binary and ternary mixture data. The study allows to obtain two main conclusions: i) as expected, the predictions of the concentrations of1and2with parameters obtained from ternary systems, give better results than those determined with parameters obtained from binary data; and ii) the NRTL and UNIQUAC models give better overall results for the systems studied.
AcknowledgEments
,,,.
Nomenclature
AWilson parameter
BNRTL parameter
Eexcess Gibbs free energy
pressure
q van der Waals area parameter
ideal gas constant
r van der Waals volume parameter
temperature
ccritical temperature
UUNIQUAC parameter
volume
xexperimental mole fraction of congener in the liquid phase (component)
ymole fraction of congener in the vapor phase (component)
expexperimental mole fraction of a congener in the vapor phase
NRTL parameter
activity coefficient
Δ interval (for temperature, pressure, and mole fraction)
percent deviation
acentric factor
Superscripts
cal calculated
exp experimental
Subscripts
,components
1 Hikari, A., Kubo, R., “Behavior of various impurities in simple distillation of aqueous solutions of ethanol”,..., 8, 294-299 (1975).
2 Lillo, M.P.I., Latrille, E., Casaubon, G., Agosin, E., Bordeu, E., Martin, N., “Comparison between odour and aroma profiles of Chilean Pisco spirit”,, 16, 59-70 (2005).
3 Lora, J., Iborra, M.I., Perez, R., Carbonell, I., “Simulación del proceso de destilación para la concentración de aromas del vino”,....., 32, 621-633 (1992).
4 Herraiz, M., Reglero, G., Herraiz, T., Loyola, E., “Analysis of wine distillates made from muscat grapes (Pisco) by multidimensional gas chromatography and mass spectrometry”,..., 38, 1540-1543 (1990).
5 Osorio, D., Perez-Correa, R., Belancic, A., Agosin, E., “Rigorous dynamic modeling and simulation of wine distillations”,.,15, 515-521 (2004).
6 Gmehling, J., Onken, U., Arlt, W., Vapor-Liquid Equilibrium Data Collection, DECHEMA, Verlag + Druckerei Friedrich Bischoff, Frankfurt (1982).
7 Valderrama, J.O., Pizarro, C., Rojas, R., “Equilibrio líquido-vapor en mezclas complejas para la simulación de procesos de destilación de mostos y vinos”,, 39, 151-156 (2001).
8 Faúndez, C.A., Valderrama, J.O., “Phase equilibrium modeling in binary mixtures found in wine and must distillation”,., 65, 577-583 (2004).
9 Faúndez, C.A., Alvarez, V.H., Valderrama, J.O., “Phase equilibrium in binary aqueous mixtures of interest in alcoholic distillation using a modified PSRK equation of state”,..., 25, 230-236 (2004).
10 Alvarez, V.H., Faúndez, C.A., Valderrama, J.O., “Vapor-liquid equilibrium in binary aqueous mixtures using a modified Regular Solution model”,...., 83, 485-492 (2005).
11 Faúndez, C.A., Valderrama, J.O., “Ecuaciones de Estado vs modelos de coeficientes de actividad para describir el equilibrio líquido-vapor en mezclas ternarias de interés en destilación alcohólica”,, 352, 141-146 (2004).
12 Walas, S.M., Phase Equilibria in Chemical Engineering, Butterworth Pub., Storeham (1985).
13 Valderrama, J.O., “The state of the cubic equation of state”,...., 42, 1603-1618 (2003).
14 Orbey, H., Sandler, S.I., Modeling Vapor-Liquid Equilibria: Cubic Equations of State and Their Mixing Rules, Cambridge University Press, USA (1998).
15 Holderbaun, T., Gmehling, J., “PSRK: A group contribution equation of state based on UNIFAC”,., 70, 251-256 (1991).
16 Faúndez, C.A., Alvarez, V.H., Valderrama, J.O., “Predictive models to describe VLE in ternary mixtures water + ethanol + congener for wine distillation”,, 450, 110-117 (2006).
17 Soave, G., “Equilibrium constants from a modified Redlich-Kwong equation of state”,..., 27, 1197-1203 (1972).
18 Wilson, G.M., “Vapour-liquid equilibrium. XI. A new expression for the excess free energy of mixing”,...., 86, 127-139 (1964).
19 Prausnitz, J.M., Lichtenthaler, R.N., Gomes de Azevedo, E., Molecular Thermodynamics of Fluid-Phase Equilibria, Prentice Hall International Series, New Jersey, USA (1999).
20 Abrams, D.S., Prausnitz, J.M., “Statistical thermodynamics of liquid mixtures: A new expression for the excess Gibbs energy of partly or completely miscible systems”,., 21, 116-128 (1975).
21 Daubert, T.E., Danner, R.P., Sibul, H.M., Stebbins, C.C., Physical and Thermodynamic Properties of Pure Chemicals: Data compilation, Taylor&Francis, London, UK (1996).
22 Chu, J.C., Getty, R.J., Brennecke, L.F., Paul, R., Distillation Equilibrium Data, Reinhold Publishing Corporation, New York, USA (1950).
23 Hausen, H., Numerical Data and Functional Relationships in Science and Technology, Volume 3, Thermodynamic Equilibria of Boiling Mixtures, Springer, Berlin-Germany (1975).
24 Fernández, M.J., Gomis, V., Loras, S., Ruiz, F., “Isobaric vapor-liquid equilibria for the system 1-pentanol + ethanol + water at 101.3 kPa”,...., 46, 665-667 (2001).
25 Conner, J.M., Paterson, A., Piggott, J.R., “Interactions between ethyl esters and aroma compounds in model spirit solutions”,..., 42, 2231-2234 (1994).
26 Conner, J.M., Paterson, A., Piggott, J.R., “Release of distillate flavour compounds in Scotch malt whisky”,..., 79, 1015-1020 (1999).
27 Conner, J.M., Birkmyre, L., Paterson, A., Piggott, J.R., “Headspace concentrations of ethyl esters at different alcoholic strengths”,..., 77, 121-126 (1998).
2008-08-26,
2009-01-04.
the Direction of Research of the University of La Serena-Chile (220-2-05 and 220-2-21), and the National Council for Scientific and Technological Research, CONICYT (FONDECYT 3020020).
** To whom correspondence should be addressed. E-mail: jvalderr@userena.cl
 Chinese Journal of Chemical Engineering2009年2期
Chinese Journal of Chemical Engineering2009年2期
- Chinese Journal of Chemical Engineering的其它文章
- Kinetics of Reactive Extraction of Nd from Nd2O3 with TBP-HNO3Complex in Supercritical Carbon Dioxide*
- Position Group Contribution Method for Predicting the Normal Boiling Point of Organic Compounds
- Experimental Study on the Initial Position Distribution of Taylor Bubbles in Cryogenic Upward Inclined Tubes*
- Enhancement of Proton Exchange Membrane Fuel Cell Performance Using a Novel Tapered Gas Channel*
- Tert-butylation of Toluene with Tert-butyl Alcohol over Realuminated H-mordenite Zeolite*
- A Fully Flexible Potential Model for Carbon Dioxide*
