对一道物理竞赛试题的解析

■张文献

对一道物理竞赛试题的解析

■张文献

一、试题提出的背景

带电粒子在电场、磁场和重力场组成的复合场中的运动规律十分典型，且该部分知识是高中物理中许多重要定理、定律、运动模型的载体，因此在高考中占有很重要的地位。近几年的高考物理试题特别是压轴题与一些竞赛题“长得很象”，将物理竞赛题改编成高考试题，虽然降低了一些难度，但仍让相当多的考生一筹莫展。现对一道不难的物理竞赛试题进行分析、引申，希望对更多同学有所帮助。

二、试题及分析

试题：如图1所示，质量为m、电量为q的带正电粒子，从垂直纸面向里磁感应强度为B的匀强磁场中由静止释放，不计空气阻力，当地重力加速度为g.试求粒子在磁场中运动的最大深度和最大速度。

分析：带电粒子在运动过程中受到重力和洛仑兹力这两个力的作用，开始时粒子在重力作用下而向下运动，粒子随后受到的洛伦兹力与速度方向垂直，且洛仑兹力的大小和方向都在随时间变化，因此粒子所受合力为变力，且合力方向与速度方向不在一条直线，粒子将做复杂的曲线运动。由于洛仑兹力始终不做功，故粒子的动能和重力势能相互转化。粒子在水平方向上受到洛仑兹力的水平分量而做变加速运动，竖直方向受到重力和洛仑兹力的竖直分量而做变加速运动。粒子运动到最大深度（即轨迹曲线最低点）处，速度方向必沿水平方向，洛仑兹力和重力的合力提供向心力，以后粒子将斜向上运动，由能量关系可知此时粒子速度最大。

三、三种解法

解法一：微元求和法.

在粒子运动轨迹上任取一点A，令粒子在此点速度为，以水平向右方向为x轴，竖直向下为y轴建立直角坐标系，将速度v分解为vx和vy，将洛仑兹力f分解为fx和fy，如图2所示。则有：

将①式两边同乘以△t（△t→0）得：

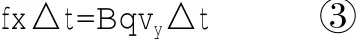
fx△t表示在极短时间△t内粒子在x方向的合力的冲量，vy△t表示在时间内粒子在y方向的位移.由动量定理知粒子从开始到运动至最低点这过程中，粒子水平方向上合力的冲量等于粒子水平方向动量的变化。

③式两边求和分别得：

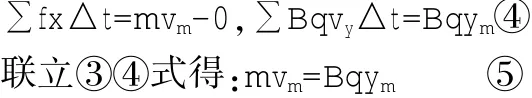
又因为粒子从开始到运动至最低点这过程中只有重力做功，故由动能定理得：

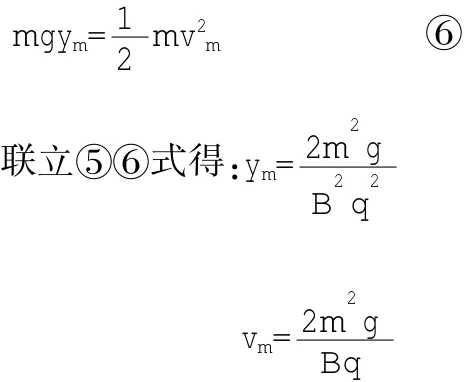
微元求和法是分析、解决高层次物理问题的常用方法。也是局部到整体的思维方法。此题粒子在x方向只受洛仑兹力的水平分量作用，微元求和后得出一个重要结论：粒子在x方向的速度改变△v与y方向的位移△y成正比，即

解法二：数学判别式法。

粒子作曲线运动到最低点时速度最大为vm，方向沿水平方向，令粒子轨迹曲线最低点的曲率半径为ρ。

则由向心力公式得：

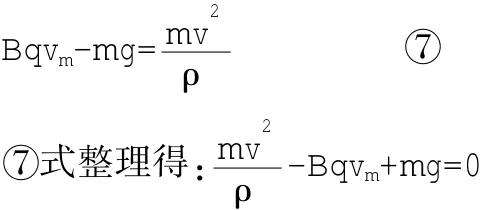
这是关于的一元二次方程，在题设条件的约束下，最低点的速度大小为唯一的确定值，故关于的二次方程判别式为零。

解法三：建立物理模型法。

粒子开始时速度为零，可设想其具有沿水平向右的速度和水平向左的速度.由于初速度为零，则和大小相等，且使对应的洛仑兹力。则粒子在以后的运动过程中受到三个力作用：重力mg，与对应的洛仑兹力，与对应的洛仑兹力.由于f1与mg相平衡，粒子在这两个力作用下做匀速直线运动，粒子所受另一个力提供向心力，使粒子做匀速圆周运动，如图3所示.则粒子的曲线运动可以看作以速度做水平向右的匀速直线运动和以速度在同一平面内做逆时针匀速圆周运动的合运动。这样在任一时刻粒子的速度是和的矢量和，曲线运动最低点即圆周运动的最低点，此时和同向故合速度最大，。粒子从开始到最低点下降的高度为圆周运动直径，即由洛仑兹力提供向心力得：由1011式得

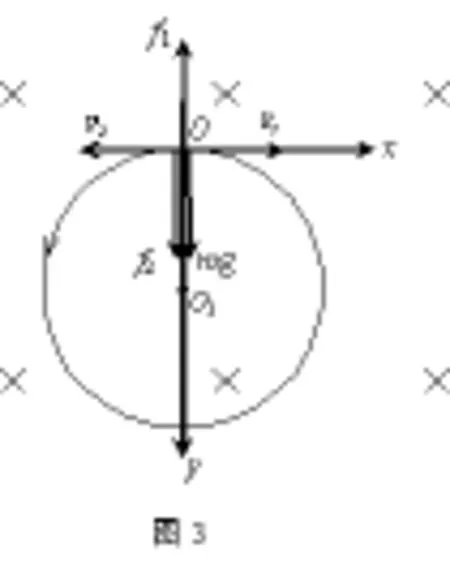
此方法关键在于建立恰当的物理模型，将复杂的曲线运动分解成两个简单运动，求解较简单。

四、试题引申：

解法三还可求出任一时刻粒子的运动轨迹坐标方程和速度方程.现提供求t时刻粒子轨迹坐标方程的解法：

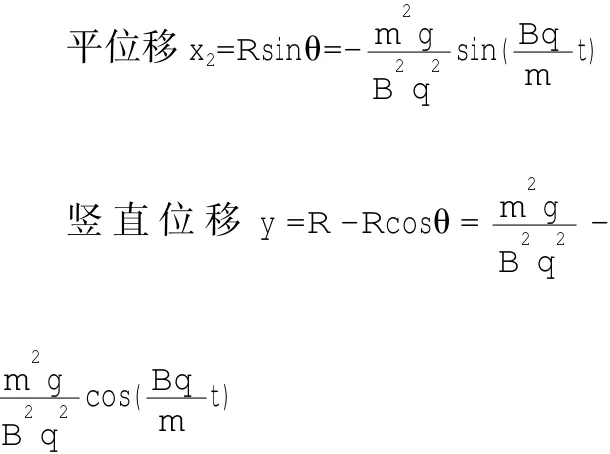
所以粒子的轨迹坐标参数方程为：

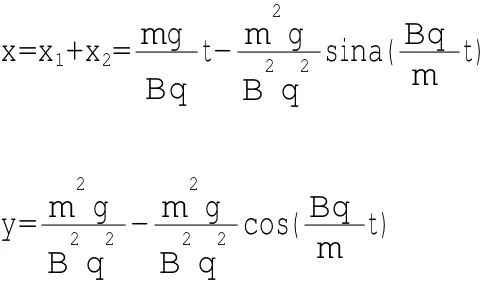
粒子的运动具有周期性，粒子的运动轨迹是一条滚轮曲线，如图5所示。

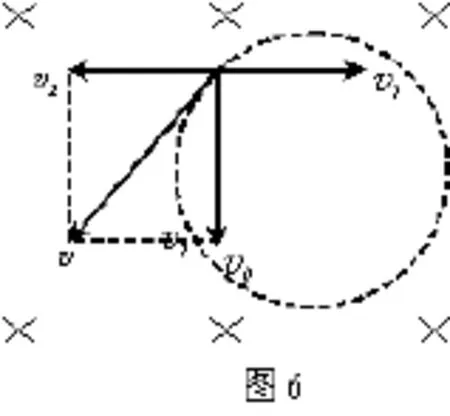
该试题中带电粒子由静止释放，如果粒子开始时就有初速度，那该怎么求解呢？这时同样给粒子附加沿水平方向向左，向右速度大小相等的速度，由于这两个方向相反速度的合速度为零，因而不影响粒子的运动，粒子以后的运动可以看作以速度v1水平向右的匀速直线运动和以速度v2与v0的合速度作匀速圆周运动的合运动，如图6所示.如果该空间还有恒定电场，又该如何来求解呢？这时可以将重力mg和电场力Eq等效成一个恒力，相当于试题中的恒力即重力来求解，这里不再赘述。

此道试题是带电粒子在复合场中运动的一道经典题目，由它可以引申出很多类型的试题。2008年江苏省高考物理试卷第14题就是改编自这道竞赛试题。对此物理竞赛试题透彻掌握了，那高考试题就迎刃而解了。老师要能把握高考命题走向，同时要有扎实的基本功，抓住问题的本质，高屋建瓴地给学生用通俗易懂的方式讲解。通过一题多解，一题多变，对学生进行物理竞赛辅导，拓宽学生的知识面，提高学生分析问题、解决问题的能力，培养学生的创新能力，有利于优秀学生的成长和提高，增强他们学习物理的兴趣，为他们日后的发展打下坚实的基础。

(作者单位：湖北省武钢三中)

责任编辑 张 泉