三体船耐波性预报

黄晓琼 陈 立 杨雄辉 周心桃

中国舰船研究设计中心，湖北武汉430064

三体船耐波性预报

黄晓琼 陈 立 杨雄辉 周心桃

中国舰船研究设计中心，湖北武汉430064

应用三维势流理论，计算了三体船在不同航速下垂荡、纵摇、横摇运动频率响应函数。预报了三体船在不规则波中各种海况下航行时的运动和加速度有义值，同时分析了三体船在西北太平洋海区一定海况下的运动特征和规律，最终根据舰船耐波性衡准要求，确定了三体船适合航行的海况与航速，为三体船耐波性方面得出了有价值的参考。

三体船；耐波性；运动响应；势流理论

1 引言

2008年4月，美国海军濒海战斗舰LCS－2三体战舰在美国Austal船厂成功下水，该舰由美国通用动力公司设计，2008年底完成海试，这是三体船型应用于舰船的又一次革命性突破。近年来，多体船船型受到越来越多国家的广泛关注，全世界范围内掀起一股研究三体船的热潮，而三体船型也逐步地由理论研究转变为实际应用。

三体船不同于常规排水型单体船，其主船体由三个部分组成，中间为主体，两舷侧各有一个侧体，三个片体相对于单体船更加瘦削细长，因此保证了其航行的快速性，而两侧侧体的吃水和浮力不断地调整，使得其具有非常好的稳定性，与同等排水量的单体舰船相比，三体船型也提高了耐波性，可在高海情下保持高速航行。

工程中常用的舰船耐波性预报方法有二维切片理论，二维半理论等［1－4］。本文将基于三维势流理论，利用Rankine源（简单格林函数）方法解决三维辐射／绕射问题［5，6］，研究了三体船在波浪中的摇荡运动以及垂向加速度。

2 三体船耐波性预报理论

耐波性指舰船在规定的海洋环境条件下能够完成任务的能力，研究三体船的耐波性能，必须从三体船在波浪中的运动开始研究，即三体船的摇荡运动［7，8］。而三体船在波浪中运动主要是三体船沿坐标轴运动的线位移和角位移、速度、加速度。

2.1 基本假定

研究三体船在波浪中的运动与单体船相似，还是需要分析三体船在规则波中的运动规律，以此找到三体船的运动与波浪之间的关系。为此，需要引入如下基本假定：

1）认为流体是不可压缩的理想流体，其表面张力效应可以忽略不计；

2）运动是无旋的，即存在速度势Φ（x，y，z，t），其梯度▽Φ（x，y，z，t）给出流体质点的速度矢量；

3）认为波浪是微幅波，水域底部以光滑水平壁面为界。

2.2 三体船在规则波中的运动

假定三体船在微幅规则波中以一定的航速和航向行驶，由于波浪的扰动而引起三体船的摇荡运动。为了更加形象地描述三体船在波浪中的运动，本文需要假定3个坐标系：

第一，空间固定坐标系OXYZ，它固定于流场中的某一位置，即原点O位于未扰动的水平面上，OZ轴垂直向上，固定坐标系不随流场或船体运动，可以反映船体在波浪中的实际运动情况；

第二，参考坐标系o′x′y′z′，随船体平均前进速度移动，不随船体一起摇荡，始终处于平衡位置。其坐标原点o′与舰船未受波浪扰动时的重心重合，三个坐标轴分别和船体的惯性轴一致，用于表征舰船摇荡运动位移和姿态的基准；

第三，半固定坐标系oxyz，随船匀速移动，原点o位于未扰动的水平面上，ox轴与三体船航行方向一致，z轴垂直向上。应用该坐标系可以直观地呈现并确定三体船在波浪中的摇荡运动，同时也可以简单实现空间固定坐标系和参考坐标系之间的相互转换。

3个坐标系的关系和位置如图1详细所示：

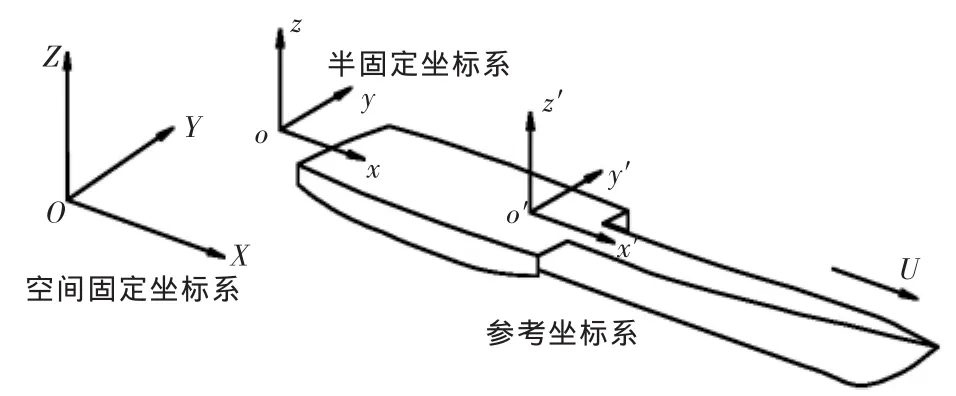
图1 描述三体船运动的坐标系

三体船沿着x方向以速度U航行，当 t＝0时，时刻点o与O重合；入射波沿－X方向传播，浪向角为β（该坐标系里β＝0°为顶浪航向，β＝ 180°时随浪航行）。当三体船无摇荡运动时，则坐标系间存在如下的坐标关系转换。

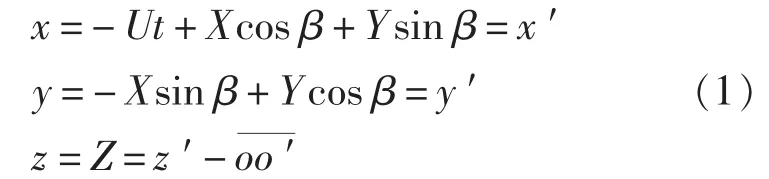
舰船的摇荡运动主要是由波浪干扰而引起的往复运动，其中在风浪中运动显著而影响严重的是垂荡、纵摇、横摇3个自由度的运动，因此它们是舰船摇荡研究的主要内容［9，10］。三体船在规则波中垂荡、纵摇、横摇运动的数学模型为：

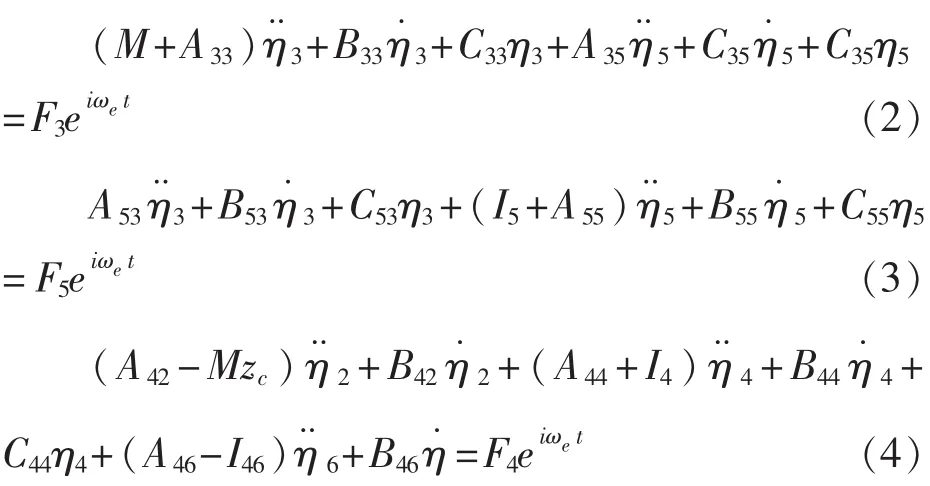
式（2）、式（3）为三体船的纵向运动方程，式（4）为三体船的横向运动方程。横向与纵向运动并不耦合，可以进行独立求解。其中：ηi为三体船的自由度；Ajk、Bjk、Cjk为附加质量、阻力系数、复原力系数；Fj为波浪扰动力；Ii为船相对于坐标轴的质量惯性矩。

3 计算结果与分析

本文研究的三体船与英国“海神”号三体试验舰外形类似，主体采用瘦削方尾船型，无球鼻首；侧体采用双向抛物线数学船型，即分别沿中纵剖面和中横剖面对称。主体与侧体船舯的纵向相对位置为46 m，两片体中心线间距为15 m。主侧体水线长的比值为8∶3，两侧体总排水量约占主体排水量的6.8%。该三体船无减摇鳍、舭龙骨等减摇设备，这样更加能反映三体船型耐波性的优劣。

首先计算三体船静水无航速状态、静水航行状态，分别进行纵倾平衡调节，同时可以得到三体船在静水中的浮态，然后计算三体船在波浪中航行的状况。图2为分析三体船运动时所需要的船体三维湿表面和自由液面网格模型：

质量模型采用全船纵向重量分布的形式，可以由沿全船中线面的很多质量点组成，质量点重量各不相同，重心高度不一，这些质量点的总重量重心与全船总重量重心一致，充分反映了三体船全船纵向重量分布的详细情况。全船重量纵向分布如图3所示：

计算时的坐标系为X轴指向船首方向，Y轴水平指向左舷，Z轴沿船中心线垂直向上，原点在主体尾柱与基线的交点处。三体船的总重量约为5 454 t，重心的X轴坐标为76.5 m，Z轴坐标为8.5 m。

图2 三体船模型

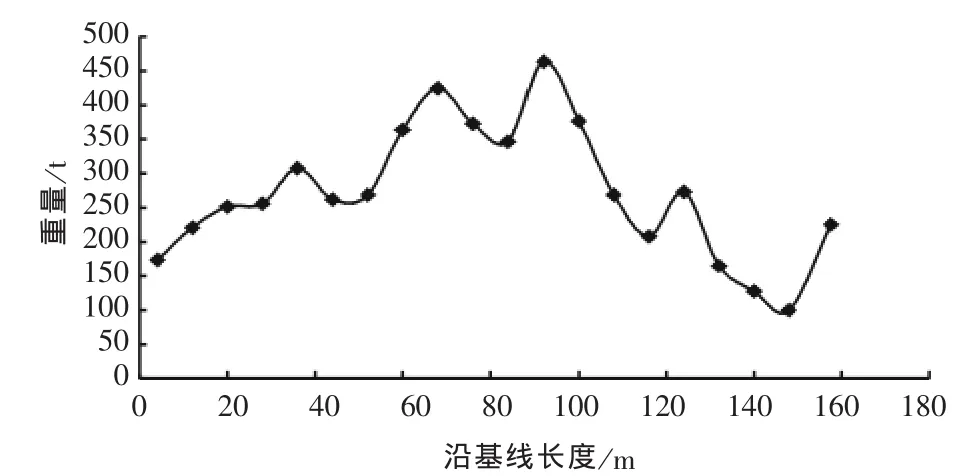
图3 三体船重量纵向分布曲线

3.1 规则波下的运动响应

该三体船的设计航速为30 kn，因此计算所取的三体船航速分别为30 kn（15.433 m／s）、25 kn（12.861 m／s）、20 kn（10.289 m／s）。选择三体船在波浪中运动的典型浪向：迎浪和艏斜浪状态，即浪向角分别为0°、30°、60°。通过计算结果发现，艏斜浪（浪向角为60°时）系统响应的传递函数幅值相对于其他两个浪向角时要大一些。因此，在此有选择性地给出了三体船在规则波中浪向角为60°时垂荡、纵摇、横摇的系统响应。具体如下：

由图4～图6中三体船规则波下稳态的系统响应传递函数曲线可以看到，三体船在规则微幅波下的垂荡、纵摇、横摇运动响应幅值随着三体船的航速（亦可是傅汝德数）不同而有一定的差异。其中三体船垂荡响应幅值极大值相对较大，纵摇响应幅值极大值数量级较小，均小于0.03，而横摇响应幅值极大值范围在0.1～0.12以内。从表1可以更加清楚直观地比较三体船这三个自由度的响应幅值极大值：

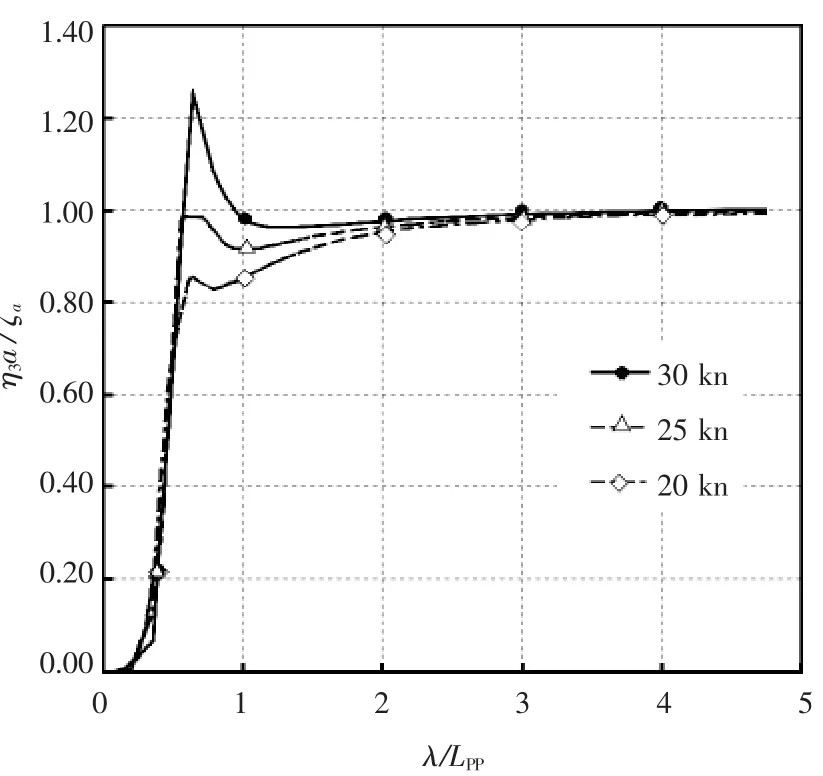
图4 60°时垂荡的传递函数

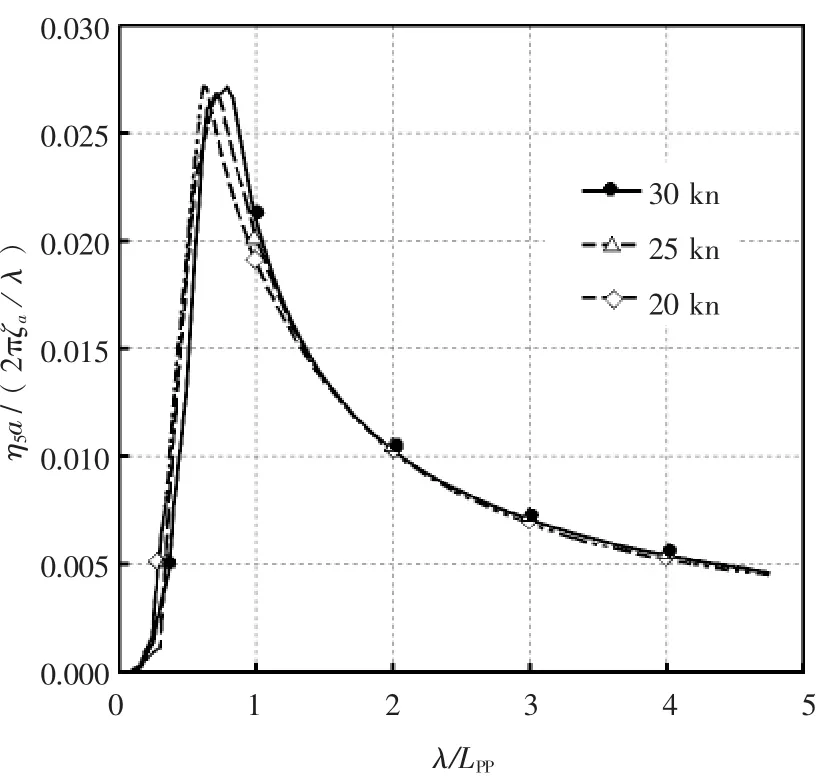
图5 60°时纵摇的传递函数

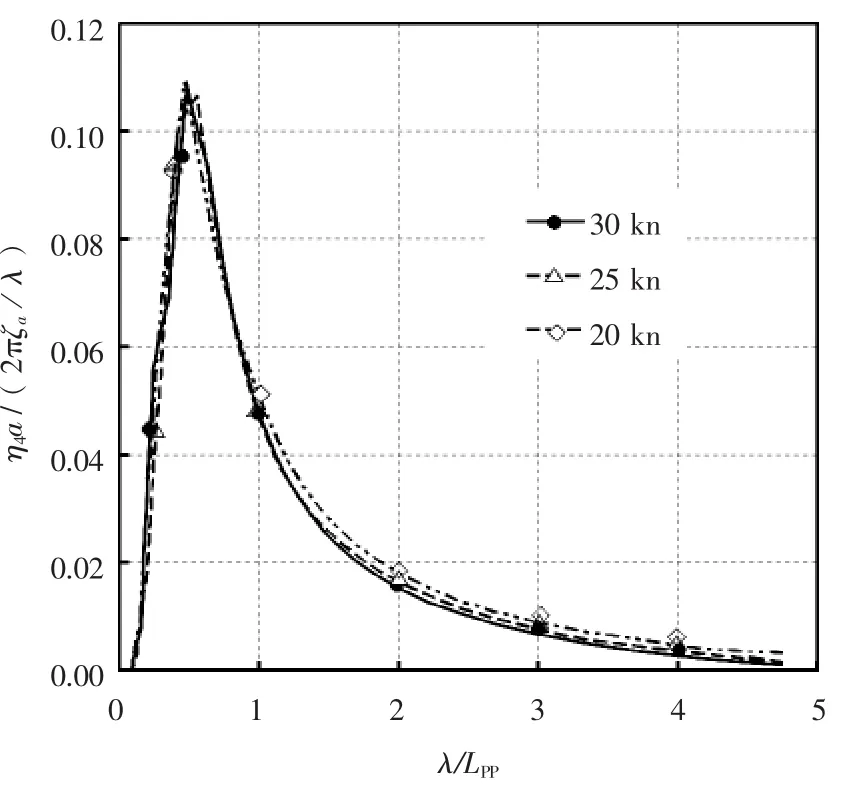
图6 60°时横摇的传递函数

表1 斜浪时摇荡运动响应幅值极值

三体船艏斜浪航行时，纵摇、横摇的响应幅值极大值分别在不同航速下近似相等，且发生在频率相近的规则波中，规则波波长均小于LPP，而垂荡的响应幅值极值有一定不同，当航速为30 kn时，最大响应幅值发生在波长小于LPP内，而25 kn、20 kn时，响应幅值极值发生在波长大于5 LPP的规则波中，最大响应幅值也趋近于1。因此，可以粗略断定，三体船特定装载状态、特定浪向角航行时，摇荡运动响应幅值极值最终也将达到稳态，即收敛在一定范围以内。

3.2 三体船在不规则波下的运动

通过海浪统计资料，确定不同海况波浪所对应的有义波高、平均周期，利用ITTC双参数谱来模拟典型海况，这样每个海况对应的即不规则波。考虑三体船在这些海况的不规则波中垂荡、纵摇、横摇运动幅值，以及特定点垂向加速度幅值。

3.2.1 海况分析与选择

目前国内建造的多体船均航行于我国沿海海域，为了使本文短期预报结果更加具有借鉴性，本文假定该三体船航行海域为西北太平洋海区。根据我国现用的海况等级划分资料和有关西北太平洋统计资料可以发现，该航行区域0～2级海况（0～0.5 m）出现的概率为7.66%，3～4级海况（0.5～2.5 m）出现的概率为 65.63%，5级海况（2.5～4 m）出现的概率为19.86%，由此可以发现西北太平洋海区里0～5级海况出现的概率为93.15%，而0～6级海况出现的概率达到99.1%，也就是考虑6级以内海况基本是考虑了该航行海域的主要海况。因此，选取如下典型波浪参数。

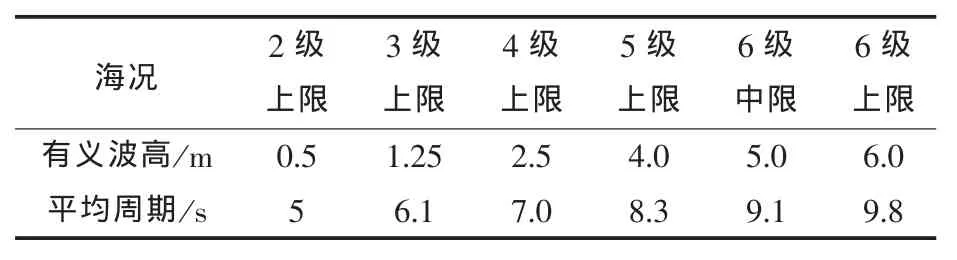
表2 海浪输入参数

波谱为ITTC双参数谱，表达式为：

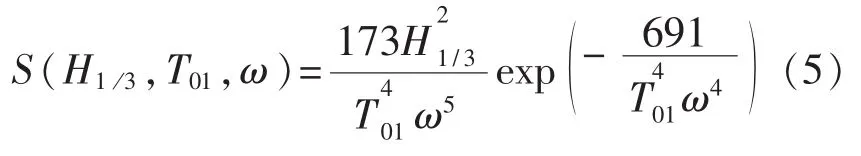
其中，H1／3为有义波高（三一有义值），m；T0为平均周期，s；ω为波浪圆频率，rad／s。

3.2.2 运动响应预报

对于船舶等线性系统，响应谱即运动与载荷的谱密度等于波浪谱密度函数乘以系统的响应幅值算子，即系统传递函数的平方，如下式：

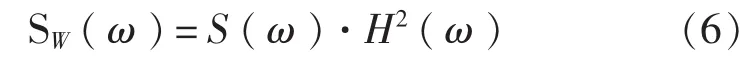
其中，SW（ω）为运动与载荷的谱密度；H（ω）为系统传递函数；H2（ω）为响应幅值算子。

本文即通过上述系统传递函数曲线以及选取的波浪谱密度曲线，确定了三体船在不规则海浪下的运动响应谱密度曲线，通过对谱密度曲线进行积分而得到运动响应的统计值。

短期海况视作均值为零的平稳正态随机过程，其幅值服从Rayleigh分布，因此三体船的运动响应谱幅值也服从Rayleigh分布，则有以下一些统计特性：

0阶谱矩m0：

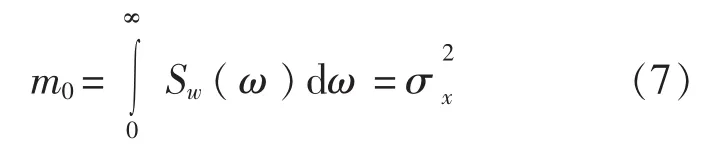
其中，σx为舰船运动响应（或运动速度、加速度）的方差。

舰船在不规则海浪上运动响应的统计值是：

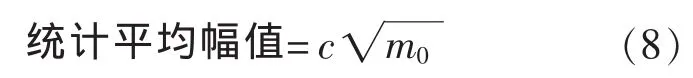
当c＝2.0时给出单幅有义值，即三分之一最大平均幅值，c＝4.0时为双幅有义值，c＝2.55为1／10最大平均值，即十一值。

有关三体船在不规则海况下的运动，表3给出部分计算结果：当航速为30 kn时，三体船在4～6级海况下迎浪和斜浪状态运动的单幅有义值。

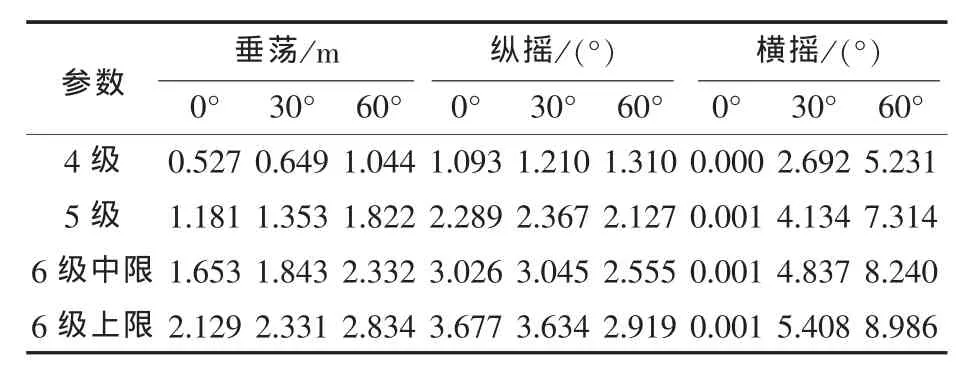
表3 航速为30 kn时运动的单幅有义值

与3.1节里的分析类似，根据最终预报的三体船在不同航速、不同浪向角时垂荡、纵摇、横摇运动幅值有义值结果里发现，当浪向角为60°（艏斜浪状态）时，该三个自由度的运动幅值相对较大。为了方便比较，图 7～图9给出三体船在不同航速时60°艏斜浪状态的垂荡、纵摇、横摇运动有义幅值。

同时，结合基本理论，选取三体船的3个重要定点来反映三体船在波浪中的运动特征，即考察三体船的桥楼（13站）处、首部0站甲板处、尾部20站甲板处的垂向加速度单幅有义值。详见表4～表6。

由表3结果可见，三体船相对于常规排水型单体船，由于增加了左右两个片体，迎浪航行时，在2～6级海况，其横摇角非常小，均不会超过0.01°，而当三体船斜浪航行时，其横摇角变化较大，其原因很显然是此时三体船左右片体吃水变化差异加剧导致重力和水动力的不平衡。在6级上限海况时，横摇角最大达到8.99°；纵摇角最大达到3.68°；垂荡幅值达到2.8 m。

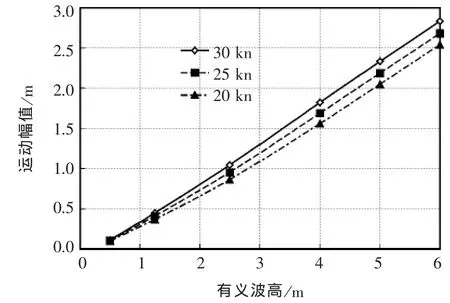
图7 不同海况下斜浪状态垂荡运动单幅有义值

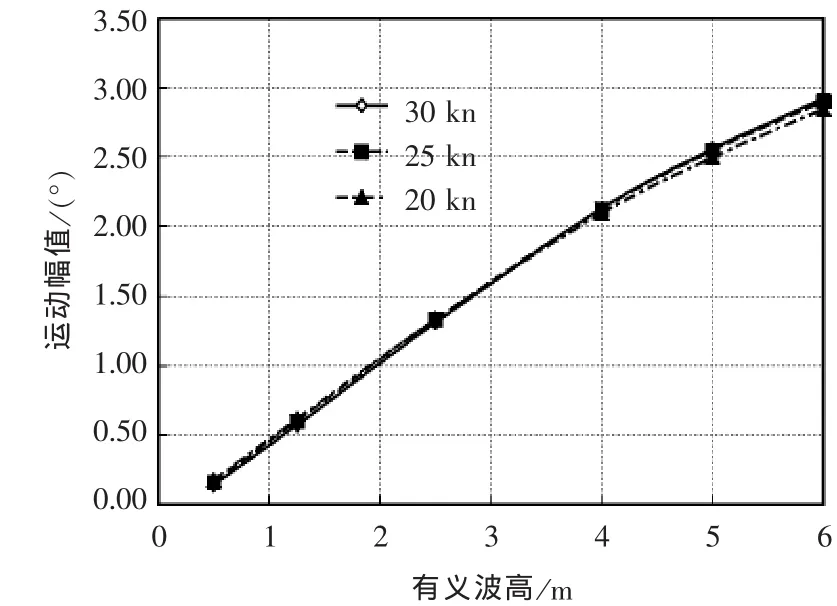
图8 不同海况下斜浪状态纵摇运动单幅有义值

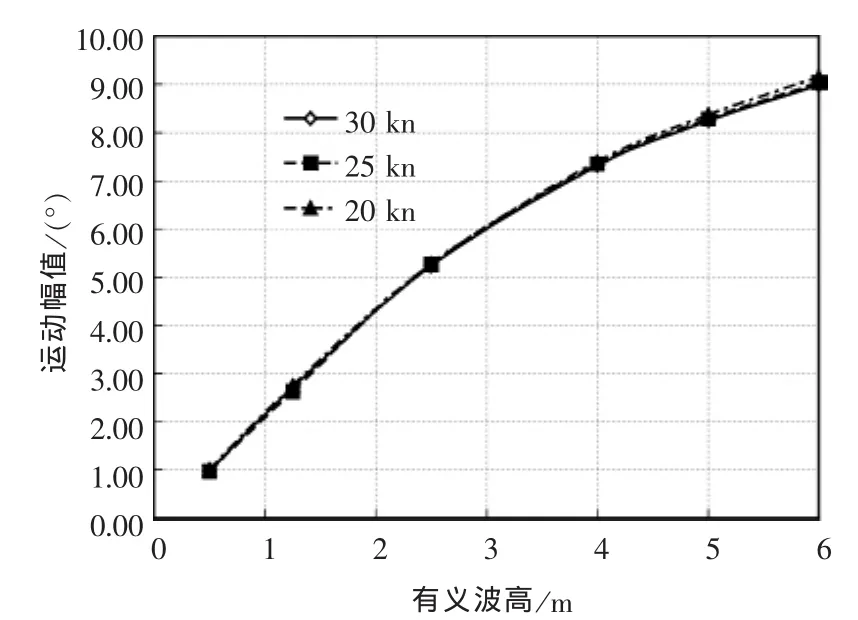
图9 不同海况下斜浪状态横摇运动单幅有义值

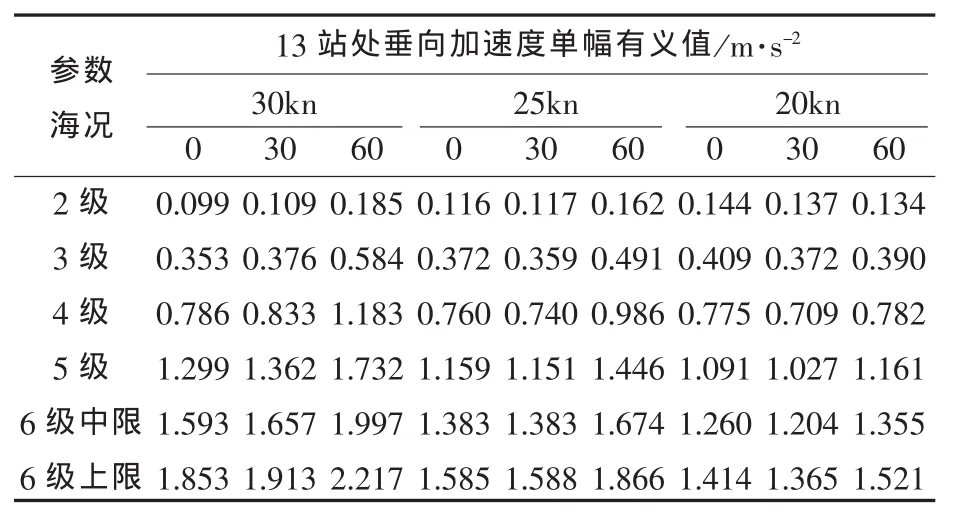
表4 桥楼（13站）垂向加速度单幅有义值

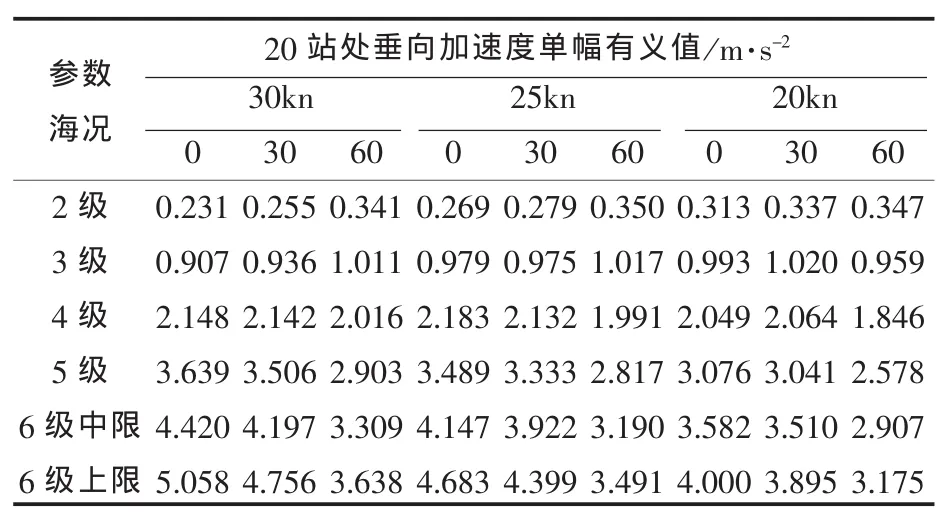
表5 20站处垂向加速度单幅有义值

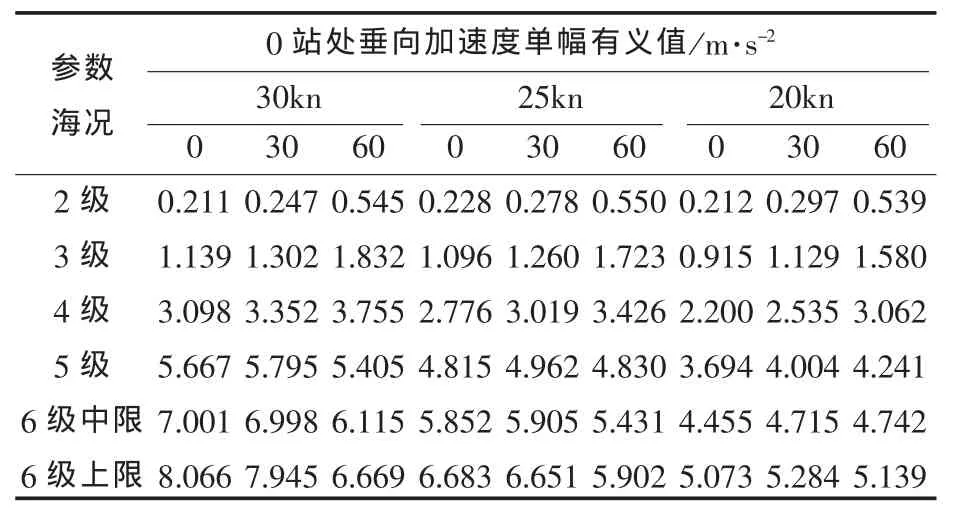
表6 0站处垂向加速度单幅有义值

由图9还可以发现，三体船在波浪中航行时，随着航速的增大，横摇角单幅有义值小幅度减小，但总体来说差别并不大。可见，航速的增加，使得三体船周围的流场发生了变化，对三体船横摇阻尼具有一定的影响。

当三体船分别在2～6级海况下斜浪航行时，随着海况级数增大，其垂荡、纵摇、横摇、桥楼（13站）处垂向加速度、20站处垂向加速度、0站处垂向加速度单幅有义值也逐步增大；航速越大，该6项的单幅有义值也越大。而选择的3个点中，随着航速、海况的变化，桥楼（13站）处垂向加速度变化范围最小，0站首柱处垂向加速度相比20站尾柱处要大一些。

在耐波性衡准要素中，通常应用6个自由度的运动幅值和特定点加速度来衡量舰船耐波性能，而特定点加速度通常利用桥楼处垂向加速度。因为这些要素直接影响到人员居住、作业的舒适性和船上载体系统正常有效工作 （直升机顺利起降、武器发射、雷达设备正常工作），包括疲劳、损伤、效能降低、功能下降、阻碍作业。采用军船耐波性衡量要求，一般军舰航渡纵摇单幅有义值3°，横摇单幅有义值小于8°，桥楼处垂向加速度单幅有义值为0.4 g（g为重力加速度）。对于纵摇而言，在西北太平洋2～6级海况里以20 kn、25 kn、30 kn速度航行时完全满足耐波性要求。对于横摇而言，在2～5级海况能满足要求，5级中限以上海况时，横摇角单幅有义值将超过8°，实际中需要采取一定的减摇措施来降低波浪中航行的横摇角。桥楼处垂向加速度的大小直接影响舰船工作人员在桥楼上的操舵、观察航线等基本工作，本文的三体船桥楼处垂向加速度在所计算的海况和航速下均满足要求。

4 结语

通过对三体船在规则波中的运动响应计算，进一步预报其在不规则波中各种海况下的运动、垂直加速度幅值有义值，总结出海况和航速对三体船运动的影响和规律，最终分析了三体船在满足规范要求情形下可以航行的海况，得出了有价值的结论，为三体船波浪中的运动预报提供了一定的借鉴性。实际中可以根据三体船的这些耐波性结果采取规避海情、降低航速、改变航向、安装减揺鳍等方法进一步来降低三体船在波浪中的摇荡运动。

［1］戴仰山，沈进威，宋竞正.船舶波浪载荷［M］.北京：国防工业出版社，2007.

［2］LIJIMA K，SHIGEMI T，MIYAKE R，KUMANO A.A prac鄄tical method for torsional strength assessment of container ship structures［J］.Marine Structures，2004，17（5）：355－384.

［3］李子富，杨盐生.船舶在规则波中纵摇与升沉运动的仿真［J］.大连海事大学学报：自然科学版，2002，28（4）：13－16.

［4］马山，宋竞正，段文洋.二维半理论和切片法的数值比较研究［J］.船舶力学，2004，8（1）：35－43.

［5］MingKang Wu，Ole A.Hermundstad，Time－domain simu鄄lation of wave－induced nonlinear motions and loads and its applications in ship design［J］.Marine Structures，2002，15（6）：561－597.

［6］戴遗山，段文洋.舰船在波浪中运动的势流理论［M］.北京：国防工业出版社，2008.

［7］EDUARDO A T，SPARANOA J V，SIMOSA A N，et al.Estimating directional wave spectrum based on stationary ship motion measurements［J］.Applied Ocean Research，2003，25（5）：243－261.

［8］盛振邦，刘应中.船舶原理：上册［M］.上海：上海交通大学出版社，2003.

［9］毛筱菲.小水线面双体船在波浪中的运动响应预报［J］.船海工程，2005（4）：3－15.

［10］JENSEN J J，MANSOUR A E，OLSEN A S.Estimation of ship motions using closed－form expressions［J］.Ocean Engineering，2004，31（1）：61－85.

Prediction on Sea-keeping Performance of Trimaran

Huang Xiao－qiong Chen Li Yang Xiong－hui Zhou Xin－tao
China Ship Development and Design Center，Wuhan 430064，China

By using 3D Potential Flow Theory，the frequency response functions for heave，pitch and roll were computed for a trimaran under various speeds.The meaningful values of motion and acceleration of the ship in irregular waves under several sea states were predicted.The motion characteristics and rules of the trimaran voyaging in the Northwest Pacific ocean under certain sea conditions were analyzed.Finally，according to the requirement for sea－keeping performance，the suitable sea states and speed were determined in this paper.The results provide a valuable reference for the study of sea－keeping performance of trimaran.

trimaran；sea-keeping performance；motion response；Potential Flow Theory

U674.951

A

1673－3185（2009）06－42－06

2008-08-25

黄晓琼（1981-），男，硕士研究生。研究方向：船舶与海洋结构物设计制造。E鄄mail：haisense@tom.com

陈 立（1963-），男，研究员。研究方向：船舶与海洋结构物设计制造

杨雄辉（1969－），男，高级工程师。研究方向：船舶与海洋结构物设计制造

周心桃（1969－），女，高级工程师。研究方向：船舶与海洋结构物设计制造