有限周期复合结构隔振系统的有限元分析

赵大为 王 勇 吴声敏 江 山 董仁义

中国舰船研究设计中心，湖北武汉430064

有限周期复合结构隔振系统的有限元分析

赵大为 王 勇 吴声敏 江 山 董仁义

中国舰船研究设计中心，湖北武汉430064

基于有限元法，研究有限周期复合结构的隔振性能。利用波动方程建立复合结构的数学模型，用有限元法对其离散，最后进行数值仿真。结果表明，有限周期复合结构的模态频率随着散射体密度的增加而减小，随着散射体直径的增大，隔振效果越好，并且有效隔振频率范围随散射体直径的增大而增大。

周期；有限元法；隔振；复合结构

1 引言

有限周期复合结构由有限尺寸的弹性材料组成，在基体中周期性地镶嵌散射体，当弹性波在受到弹性常数及密度的周期性调制时，会产生弹性波带隙，即在一定频率范围内的弹性波的传播将被抑制或禁止。因此，有限周期复合结构在舰船低频减振降噪［1－3］、抗冲击［4］、水下结构设计［5］、振动滤波器、新型传感器等方面，具有广泛的应用前景。

有限元方法自20世纪50年代创立以来，在舰船研究领域内得到了广泛的应用［6－10］。有限元法基于集中质量思想，在低频范围内具有收敛好、易于计算复杂结构等优点。本文试图利用有限元法对有限周期复合结构进行分析，并对其隔振性能做了初步评估。

2 有限周期复合结构模型和假设

本文所研究的周期复合结构如图1所示。图中给出坐标轴x1和x2的方向，x3方向垂直于纸面向上。为了分析的方便起见，图1中已经人为地将复合结构周期地划分为单层结构。阴影部分A为基体材料，其中周期插入了球状散射体B，其直径均为d。其间距a为x1方向的晶格常数，b为x2方向的晶格常数，h为x3方向的晶格常数。本文仅讨论该周期复合结构沿x1方向的隔振效果，为了后面的计算方便，作如下假设：

图1 有限周期复合结构示意图

1）外激励力为简谐函数，且沿x1方向垂直入射到周期复合结构上；

2）基体A和球状散射体B由均匀、各向同性、连续材料组成。

3 有限周期复合结构系统的运动方程

以左下角第一个球状散射体的球心为坐标原点，球状散射体B的中心在x1，x2，x3上的坐标为（ma，nb，lh），其中m，n，l＝0，±1，±2，…。设外激励力大小为F（u1）eiωt，则系统的运动微分方程为：

式中，u1，u2分别为沿 x1，x2轴方向的振动位移；λ，μ为材料的拉梅（Lame）常数；ρ为材料密度。

在周期复合结构层与层之间的边界处必须满足两点假设，即位移u1连续和应力张量T1连续。

波动方程式（1）的位移场解可以表示为：

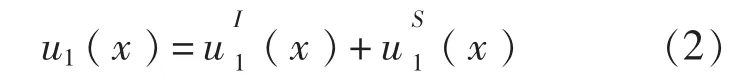
外激励力作用到周期复合结构上，能量通过弹性波的形式传播，于是有：

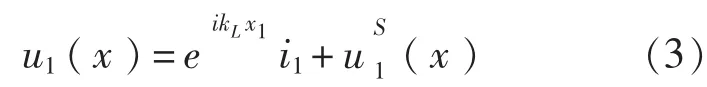
式中，i1代表沿坐标轴x1方向的单位矢量；kL为弹性波的波数，kL＝。

由球状散射体关于x2和x3的周期排列，以及散射体表面的零作用力，使得uS1（x）的周期形式可以在x2和x3坐标上用指数傅立叶级数来表示。为了写出该级数的一般表达式，这里采用常用的位移分解方法，将u（x）表示成标量势函数φ（x）和矢量势函数ψ（x）的形式［4］：

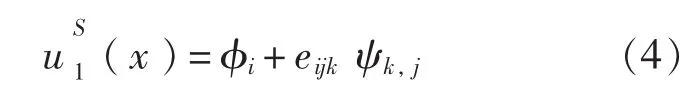
式中，φ（x）和ψk（x）分别满足含纵波波速kL和横波波速kT的波动方程：

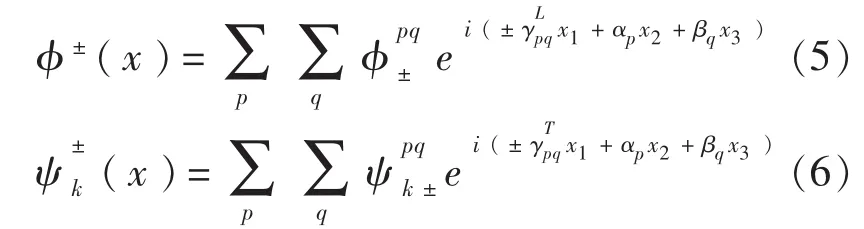
式中，角标“＋”的应用范围为x1＞0，角标“－”的应用范围为x1＜0；

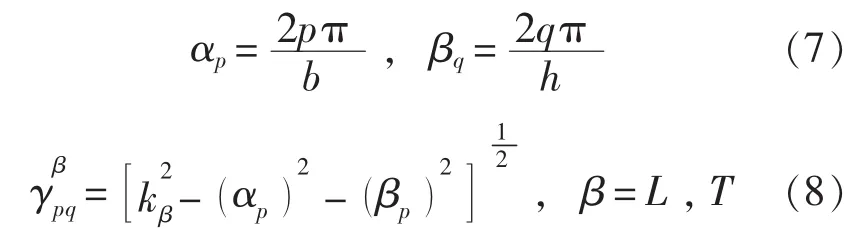
式中，弹性横波波数kT=；弹性横波波速cT=

对于小阻尼结构，弹性波波数为：

式中，ηs为材料的结构损耗因子。

为了对有限周期复合结构进行有限元分析，将弹性波波动方程式（1）写成矩阵形式，即：

式中，微分算子

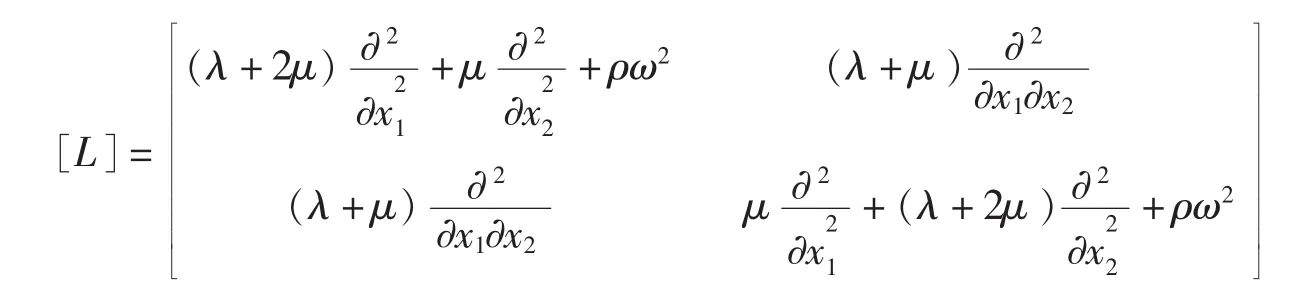
4 有限周期复合结构的有限元分析

4.1 网格划分

图2是3×3周期复合结构示意图。本文采用ANSYS有限元分析软件，选择四面体单元Solid 45并用自由网格对所研究的周期复合结构划分网格，图3为其网格划分结果。为了显示方便，将基体和内嵌散射体分开表示，其中图3（a）表示基体的网格划分结果，图3（b）表示内嵌散射体的网格划分结果。

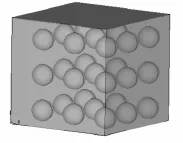
图2 3×3周期复合结构示意图

图3 3×3周期复合结构的网格划分

由于基体与内嵌散射体是独立的两个实体，因此，在网格划分完成以后，还需要解决各单元的联结问题。一般是将各单元重复的结点进行合并，使位移和力能够通过结点传递下去。

4.2 迭代算法步骤

下面将本文采用的有限单元法和中心差分法逐步求解有限周期复合结构振动位移的算法步骤归纳如下：

1）根据单元结点坐标和单元位移｛u｝（r）（r＝1，2，…）建立单元局部坐标系；

6）各单元作用到结点上的力，｛F（u）｝（r）＝（式中负号代表反作用力），得到不平衡力，｛ΔF（u）｝（r）＝｛F（u）｝＋｛F（u）｝（r）＝

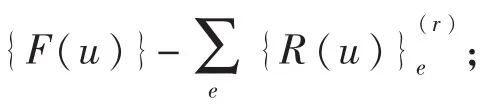
7）求解结构平衡方程，［K］（r）｛Δu｝（r＋1）＝｛ΔF （u）｝（r），得到第r＋1次迭代的位移增量｛Δu｝（r＋1），于是｛u｝（r＋1）＝｛u｝（r）＋｛Δu｝（r＋1）；

8）给出位移、速度和加速度t＝0时刻的初始条件，u0，˙0，¨0；

9）选择时间步长Δt，并计算积分常数c0＝

10）将积分常数代入式（1），每次迭代完成后增加一个时间步长Δt，一直计算到时刻t，即可得到第r＋1次迭代的振动位移；

11）反复迭代，直到收敛条件｛ΔF｝趋近于0，否则返回到第1）步继续运算。

5 结果分析及讨论

计算时所用主要参数选取：晶格常数a＝0.05 m，b＝0.05 m，h＝0.05 m；基体材料为硅橡胶，其密度为ρA＝1 300 kg／m3；拉梅常数λA＝6×105Pa，μA=4×104Pa，弹性模量EA＝7.84×106Pa，泊松比vA＝0.47；球状散射体分别为铜和铝，其主要材料属性为 ρCu＝8 356 kg／m3，拉梅常数 λCu＝1.726×1010Pa，μCu＝7.527×1010Pa，弹性模量ECu＝1.08×1011Pa，泊松比vCu＝0.31；ρAl＝2 799 kg／m3，拉 梅 常 数 λAl＝5.895 5×1010Pa， μAl＝2.681 2×1010Pa，弹性模量EAl＝6.8×1010Pa，泊松比vAl＝0.32。对系统进行简谐激励，激励点的位置在坐标（0，0.075，0.075）处，且其位移激励的幅值为0.001 m；输出点的位置在坐标（0.15，0.075，0.075）处。

5.1 数值仿真结果

本文对三维3层周期复合结构隔振系统进行数值仿真，即n＝3。

表1列出了本文所研究的有限周期复合结构当散射体直径为d＝0.03 m、材料分别为Cu和Al时的前10阶模态频率。

散射体直径分别为d＝0.02 m、0.03 m和0.04 m时周期复合结构的振动传递率随频率f的变化曲线如图4～图6所示。其中图（a）和图（b）表示散射体分别为铜和铝的情况，并且实线表示无阻尼时的情况，短虚线表示考虑橡胶的阻尼系数为0.000 1的情况，长虚线表示考虑橡胶的阻尼系数为0.000 5的情况。

5.2 数值仿真结果讨论

从表1可以看出，有限周期复合结构的模态频率随着散射体密度的增加而减小。从图4～图6可以看出，周期复合结构的基频随着散射体直径的不同而不同，且随散射体材料的不同而变化不大。当散射体直径由0.02 m增加到0.04 m时，振动衰减率的极值也逐渐减小，由－17dB降到－28 dB以下，即随散射体直径的增大振动衰减越厉

表1 有限周期复合结构前10阶模态频率

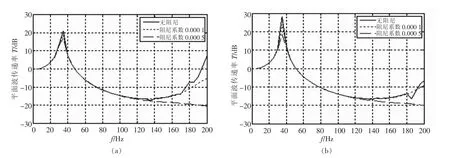
图4 散射体直径d＝0.02 m时周期复合结构的隔振性能曲线图

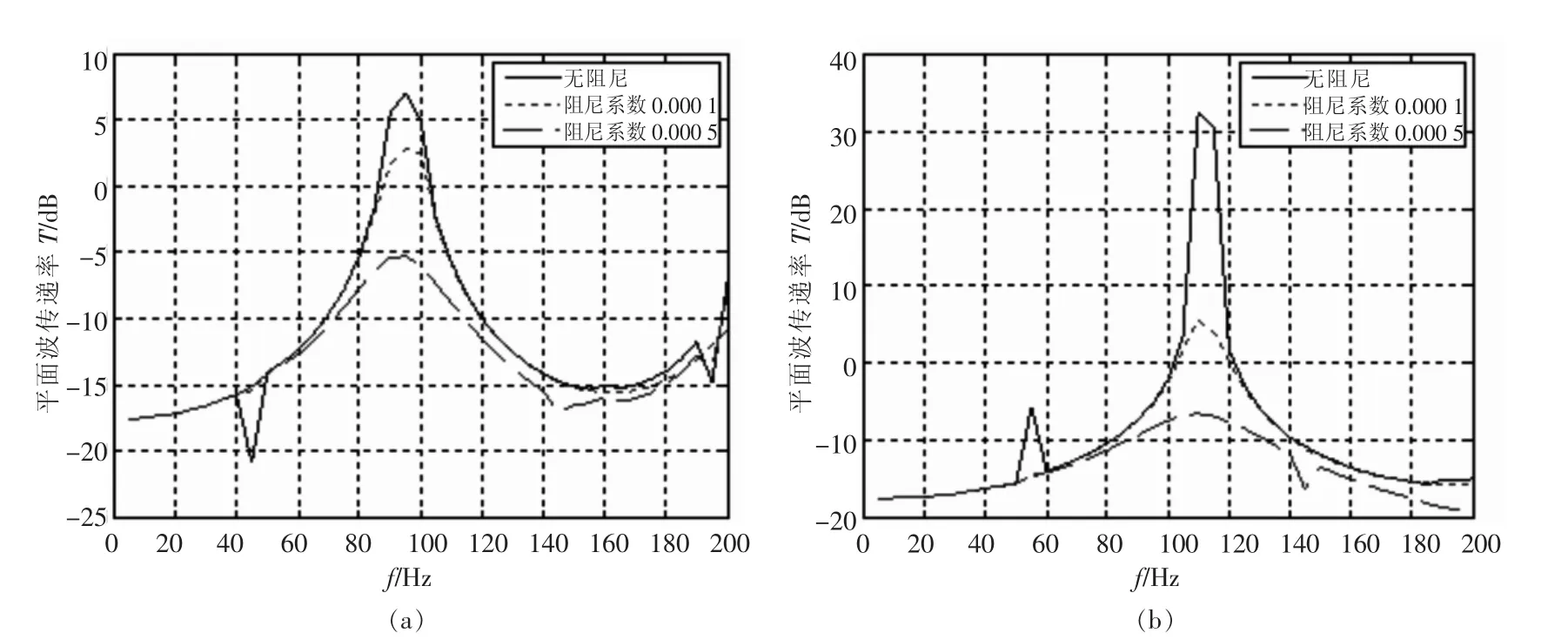
图5 散射体直径d＝0.03 m时周期复合结构的隔振性能曲线图

图6 散射体直径d＝0.04 m时周期复合结构的隔振性能曲线图

害。在低频范围内，当散射体直径为0.02 m时，周期复合结构的有效隔振频率范围为46～190 Hz；而当散射体直径增大到0.04 m时，周期复合结构的有效隔振频率范围为39～200 Hz以上。为此，可以得出有利于工程设计的一些结论。

1）有限周期复合结构的模态频率随着散射体密度的增加而减小；

2）周期复合结构的基频随着散射体直径的不同而不同，且随散射体材料的密度不同而有所变化；

3）随着散射体直径的增大，周期复合结构的减振效果越来越好；

4）周期复合结构的有效隔振频率范围随散射体直径的增大而增大。

［1］温激鸿，王刚，刘耀宗，等.金属／丁腈橡胶杆状结构声子晶体振动带隙研究［J］.振动工程学报，2005，18（1）：1－7.

［2］吴福根，刘正猷，刘有延.二维周期性复合介质中弹性波的能带结构［J］.声学学报，2001，26（4）：319－323.

［3］SIRVENT R E，COCOLETZI G H.Band structure for the propagation of elastic waves in superlattices［J］.Journal of the Acoustical Society of America，1994，95（1）：86－90.

［4］李青，吴广明.水面舰艇舷侧抗冲击防护结构形式初探［J］.中国舰船研究，2008，3（3）：26－29.

［5］董仁义，吴崇健.水下翼型水动力学与声学研究进展［J］.中国舰船研究，2008，3（3）：1－9.

［6］徐张明，沈荣瀛，等.利用FEM／IBEM计算流体介质中的壳体的结构声耦合问题［J］.振动工程学报，2002，15（3）：363－367.

［7］邹元杰，赵德有.水下结构声固耦合振动的特征值计算［J］.船舶力学，2004，8（2）：109－120.

［8］邹元杰，赵德有.按可压缩流体计算结构响应对声辐射的影响［J］.大连理工大学学报，2004，44（1）：85－90.

［9］徐张明，汪玉，华宏星，等.船舶结构的建模及水下振动和辐射噪声的FEM／BEM计算 ［J］.船舶力学，2002，6（4），89－95.

［10］曾革委.潜艇结构水下声辐射及其控制研究［D］.中国舰船研究设计中心博士后工作站，2005.

Finite Element Analysis of Vibration Isolation System for the Periodic Composite Structure

Zhao Da-wei Wang Yong Wu Sheng-min Jiang Shan Dong Ren-yi
China Ship Development and Design Center，Wuhan 430064，China

Based on finite element method and central difference method，the vibration isolation performances of finite periodic composite structure are studied.The mathematical model is established by the wave equation.The structure is discreted by finite element method and central difference method.Finally，numerical simulation is carried out.The results show that the modal frequencies of the structure decrease with the increase of the density of the inner scatterers，the effect of vibration isolation gets better with the increase of the diameter of the inner scatterers，and the effective frequency ranges of vibration isolation get wider with the increase of the diameter of the inner scatterers.

period；finite element method；vibration isolation；composite structure

O328，TH113.1

：A

：1673－3185（2009）01－43－04

2008－05－04

赵大为（1982－），男，工程师，硕士研究生。研究方向：船舶系统。E-mail：zdw1811＠yahoo.com.cn

王 勇（1974－），男，工程师，博士。研究方向：船舶系统