“斐波那契”狂想

魏小山

● 教学内容分析

看到这个课题，很多人都会误认为这是数学课。其实，它是信息技术校本课程中的一课。开设信息技术校本课程，不少信息技术教师都会选择类似信息技术前沿探究、动画处理、网页制作和视频处理等专题，这些内容虽然从一定程度上延伸了信息技术课堂，但总体让人感觉缺乏新意，对学生的吸引力也不足。于是，我从创意入手，设计了一系列专题课程，自己编写教材，让学生在生动而富有创意的课堂内容中，潜移默化地学会如何用所学的知识来解决学习、生活中遇到的问题，更重要的是学会如何学习。《“斐波那契”狂想》就是系列专题中的精彩一课。

● 教学对象分析

教学对象是高一年级学生，他们在义务教育阶段进行了较为系统的信息技术课程的学习，基本掌握了文本、多媒体的采集与加工技术，但从未上过信息技术校本课程，对该课程充满好奇。此外，由于数学课程还未讲授“斐波那契数列”的相关知识，绝大多数学生对该内容不了解，有利于课题的引入及情境的创设。

● 教学目标

了解“斐波那契数列”所涉及的各领域的知识，学会用其解决学习、生活中遇到的问题。

学会利用信息技术提高工作效率，美化生活。

摆正学习态度，将学习放眼于个人的全面发展，而非功利化的考试目的。

● 教学过程

（一）揭密“斐波那契”

1.什么是“斐波那契”

师：“斐波那契”是一个人名，他是意大利著名的数学家。1202年，他撰写了著名的《算盘书》。在这本书中记载了一个世界著名的数学问题，叫作“兔子问题”。

设计意图：刚刚踏入高一的学生对“斐波那契”并不了解，而专题的名称“‘斐波那契狂想”让学生感到非常好奇。因此，课堂从对“斐波那契”的揭密开始，进一步通过“兔子问题”深入探讨斐波那契数列。

2.“兔子问题”呈现

师：我们一起来看看“兔子问题”（见图1）：假设有一对兔子，从出生后第3个月开始，每个月都生一对小兔子。小兔子到第三个月又开始生下一代小兔子。假设兔子只生不死，每个月各有多少对兔子？

学生打开Excel，模仿效果图，建立表格，尝试计算12个月的兔子对数，并填入表中，然后观察计算出来的数据有什么规律。

设计意图：在这个环节中先将“兔子问题”抛出来，让学生尝试通过自己的思考来解决问题。

在毫无提示的情况下，要完全算出12个月的兔子对数有一定难度，这为下个环节的分析埋下伏笔。

3.动画演示，揭示奥秘

师：通过动画演示算出前7个月的兔子数。第1个月，有1对兔子；第2个月，因为兔子还不能生育，仍然是1对兔子；第3个月，大兔子生了一对小兔子，栅栏里有2对兔子；第4个月，大兔子又生了一对小兔子，而上月出生的小兔子还不能生育，栅栏里有3对兔子；第5个月，原来的大兔子又生了一对小兔子，而第3个月出生的兔子已经成熟，也生了一对小兔子，这时共有5对兔子……我们将前7个月的兔子数列在表中，观察这组数有什么特点。

生：从第3个月开始每个月的兔子数都是紧临的前两个月兔子数之和。

师：发现这个规律后，你能快速告诉我8～12月的兔子数吗？请同学们继续完成表格的填写，看看谁填得最快，并告诉我第12月的兔子数是多少。

学生按照规律，在Excel表格中填写每个月的兔子对数。做得快的学生已经忍不住喊出了最终的结果：“第12个月的兔子数是144对。”

师：这12个月兔子对数形成的数列就是世界上非常有名的“斐波那契数列”。它的定义是：若一个数列，首两项等于1，而从第三项起，每一项是前两项之和，则称该数列为斐波那契数列。斐波那契本人并没有把“兔子问题”和“斐波那契数列”看得特别重要。在《算盘书》中，“兔子问题”只不过是书里许多问题中并不特别的一个。但是，在以后的岁月中，这个数列似乎和高产兔子一样，引发了为数众多的数学论文和介绍文章。“斐波那契数列”成为数学中最奇特和最常出现的数列。美国数学家出版了一份专门研究它的季刊，称为《斐波那契季刊》（Fibonacci Quarterly），里面登载了关于这种数列最近新发现的性质。

刚才，我观察到大多数同学都是通过手动输入的方法，在Excel表中列出兔子对数的，幸好列出是12个月的兔子数，要是列出200个月的兔子数，我相信不少同学就会皱眉头了。这种低效方式显然不能满足我们的需要。既然使用计算机，我们就要发挥出它的优势来，所以，我们要思考一种方法可以快速完成任务。

根据所总结出来的数列规律，在Excel中运用公式，快速算出结果。具体操作见图2：在第3个月的兔子数中输入“＝1＋1”，在第4个月的兔子数中输入“＝2＋1”，我们发现并没有提高效率，反而使效率更低了。有没有更简便的方法，能够通过公式复制完成而不必一个一个地输入公式呢？那就是“公式＋引用单元格”的方法。具体操作：在第3个月的兔子数中输入“＝B2＋B3”，然后用“填充柄”进行公式复制，快速求出结果，浏览单元格，发现单元格数会自动累加，这就是公式复制的快捷之处。

学生用公式复制的方法，尝试列出12个月和50个月的兔子对数。

设计意图：在这个环节中，学生可以充分领略到数学的魅力，同时，还学会了如何用信息技术来解决数学问题。用信息技术解决问题的方法多种多样，还要学会寻找最优的方法来解决问题。

4.编制程序计算兔子对数

师：用Excel的公式复制解决兔子问题，我们已经觉得很方便了，其实还有一种更为高效的方法，能立即呈现结果，就是用编程的方法来解决问题。

程序演示：点击按钮就能迅速呈现出12个月的兔子对数。（见图3）

分析源程序：第1行语句定义数组；因为斐波那契数列的规律是从第三项开始的，所以，我们把前两项数组赋值为1，并将它们打印出来，然后，通过一个循环语句，利用递推关系式计算出随后10个月的兔子对数，并依次将结果显示在屏幕上。

操作演示：新建工程，放置按钮，双击按钮复制代码，运行测试效果，保存生成可执行程序。

学生在VB中添加窗口、按钮并撰写代码，尝试改变月份数为50，解决窗口运行呈现问题。

设计意图：本环节掀起本课的一个小高潮。学生此刻已经深深被信息技术的魅力所吸引。短短的几句代码就能实现如此神奇的效果，让还没接触编程的高一学生毫无障碍地“摘到桃子”，享受到成功的喜悦。

（二）探索大自然中的斐波那契数列

师：在自然世界中，植物似乎对斐波那契数着了迷。植物的花、叶、枝条、果实、种子等形态特征，都可发现斐波那契数。最典型的例子就是以斐波那契螺旋方式排列的花序或树叶。蓟的头部具有13条顺时针旋转和21条逆时针旋转的螺旋，还有我们食用的蔬菜，如青菜、包心菜、芹菜等的叶子排列也具有这个特性。观察向日葵的花盘，我们会发现其种子排列组成了两组相嵌在一起的螺旋线，一组是顺时针方向，一组是逆时针方向。再数数这些螺旋线的数目，虽然不同品种的向日葵会有所不同，但是每组数字都是斐波那契数列中相邻的两个数。再看看菠萝、松果上的鳞片排列，虽然不像向日葵花盘那么复杂，也存在类似的两组螺旋线，其数目通常是8和13。有时候这种螺旋线不是那么明显，需要仔细观察才会注意到。（见图4）

数学家泽林斯基发现树枝生长的“斐波那契”规律。他说，当你漫步在树林之中时，你会发现：由于新生的枝条往往需要一段“休息”时间，供自身生长，而后才能萌发新枝。所以，一株树苗在一段间隔，如一年，以后长出一条新枝；第二年新枝“休息”，老枝依旧萌发；此后，老枝与“休息”过一年的新枝同时萌发，当年生的新枝则次年“休息”。这样，一株树木各个年份的枝桠数，便构成斐波那契数列。这个规律，就是生物学上著名的“鲁德维格定律”。

植物有这种生长特性，难道是因为这些植物懂得斐波那契数列？当然不是，是因为这样的布局能使植物的生长疏密得当、最充分地利用阳光和空气，所以，很多植物都在亿万年的进化过程中演变成了如今的模样。当然，受气候或病虫害的影响，真实的植物往往没有完美的斐波那契螺旋。但是，我们可以借助计算机来绘制完美的斐波那契螺旋。

设计意图：大自然中的植物如此钟爱斐波那契数，给学生带来了不小的震撼。学生在欣赏自然美的同时，学习了如何通过软件绘制完美的斐波那契螺旋。

（三）斐波那契与黄金分割

师：为什么植物如此偏爱斐波那契数？这和另一个更古老的、早在古希腊就被人们注意到甚至去崇拜它的另外一个“神秘”数字有关。图5有几个长方形，比较一下它们的大小形状，你认为哪一个形状最好看呢？

生：选E！选A……

师：在100多年前，德国的一个心理学家文特做了这样一个试验，它把这些形状各异的长方形给很多人选择，结果，几乎所有的人都选择了图形E。尤其是文化素养越高的人，这种爱好就越集中。图形E的长方形的宽与长的比大约是2∶3，这个比例常被人们称为“黄金分割比”。

黄金比的研究可追溯至公元前的古希腊时期，它的定义是：设AB是一条线段，今将线段AB分割成两段，使短段：长段＝长段：全段。这样的分割方式叫做黄金分割，而这一比值就称为黄金比，也就是0.618∶1，0.618被数学家称为“黄金数”（见图6）。

同学们还记不记得，用直尺和圆规如何找出黄金分割点？

学生在黑板上绘制，过B点作一条直线垂直AB，然后在这条直线上取线段BD，使得BD的长是AB的一半，然后我们联结AD。我们再以D为圆心，DB的长为半径画一个弧。这个弧交AD于E点，然后，再以A为圆心，AE的长为半径画弧，这个弧交AB于C点，C点就是我们所要找的将AB黄金分割的点。

师：前面老师讲到，与斐波那契相关的古希腊崇拜的“神秘”数字就是黄金数。它们彼此有什么关系呢？同学们发现没有，如果我们计算相邻两个斐波那契数的比，它们越来越接近黄金分割比0.618∶1。我想植物喜爱斐波那契数，实际上是因为喜爱黄金数。这是为什么呢？也许是上帝想让世界充满美与和谐吧。其实，黄金分割比在几何、大自然、艺术、生活中处处可见。黄金三角形：顶角为36°角的等腰三角形，其底与腰之比恰为黄金比。（见图7）大自然的鬼斧神工处处都留下了黄金分割的痕迹：枫叶的叶脉和叶子宽度的比例，蝴蝶身长和翅宽的比例都成黄金比例0.618。此外，以0.618为比例扩张的螺旋也被成为黄金螺旋（见图8）。你有没有注意到，电视新闻播报时，主播的位置经常被安排在画面的黄金分割点，而非正中央。

在艺术领域里更是神奇。蒙娜丽莎完美的黄金比例，流露着庄严、和谐、神秘的气质；芭蕾舞演员顶起脚尖，正是为了使人体的上下身之比更符合黄金比。像二胡、提琴这样的弦乐器，当乐师们把它们的码子放在黄金分割比的分点上时，乐器发出的声音是最动人美丽的。同学们，你们知道吗？我们的国歌《义勇军进行曲》的高潮部分正好处在全曲的黄金分割点上，所以，我们在唱国歌的时候也在分享着黄金分割的魅力。建筑师们早就懂得使用黄金分割比了。在公元前3000年建成的埃及法老胡夫的金字塔（埃及金字塔为正四角锥体，塔高与底部正方形边长之比为黄金比，足见公元前两千多年的人们就已经发现了黄金比）和公元前432年建成的雅典帕特农神庙就采用了这个神奇之比。因此，它们的整个结构以及它们与外界的配合是那样的和谐美观。据研究，从猿到人的进化过程中，骨骼方面以头骨和腿骨变化最大，躯体外形由于近似黄金比而变化最小。古希腊人早就发现了这个人体比例的奥秘并将它充分运用于艺术雕塑中。维纳斯雕像，象征着爱与美的女神，被视为女性体型美的标准。人的肚脐位于人体身高的黄金分割点。肚脐以上，颈部是黄金分割点；肚脐以下膝盖是黄金分割点。还有，人在精神愉快时的脑电波频率下限约8赫兹，上限约12.9赫兹，上下限之比近于黄金比。舒张压与收缩压之比近似黄金比。难怪符合此比例的人、事物都非常顺眼。

（四）抢答互动环节

师：请回答以下问题：

（1）报幕员应站在舞台的什么地方报幕最佳？

生：根据黄金分割，应站在舞台宽度的0.618处。

（2）高清晰度电视的屏幕为什么要设计成16∶9？

生：因为若将屏幕的长与宽组成一条线段，取这条线段的黄金分割点，将线段分成两条线段，则屏幕的长与宽刚好接近它。

（3）请问大热天开空调应调在什么温度最佳？

生：人的正常体温是37.5度，37.5×0.618=23.175，这个温度最佳。

（4）为什么许多国家都喜欢在国旗上绣五角星？

生：因为五角星是很美的几何图形，其中由五条线段相交的五个点刚好是这五条线段的黄金分割点。

设计意图：由斐波那契数列引出与其密切相关的“黄金分割”，“黄金分割”在大自然和人类生活中所呈现的美，让学生叹为观止。

（五）课外拓展

师：斐波那契数列有许多奇妙的性质，其中有一个性质是这样的：

F_n-F_n+1·F_n-1=（-1）ⁿ⁺¹（n＞1）

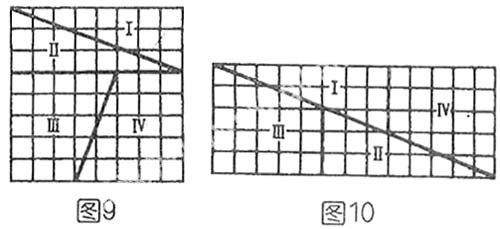
斐波那契数列的这个性质，常被用来构造一些极为有趣的智力游戏。美国《科学美国人》杂志刊载过一则故事：一位魔术师拿着一块边长为8英尺的正方形地毯，对他的地毯匠朋友说：“请您把这块地毯分成四小块，再把它们缝成一块长13英尺、宽5英尺的长方形地毯。”这位匠师对魔术师算术之差深感惊异，因为，两者之间面积相差达一平方英尺呢！可是魔术师竟让匠师用图9和图10的办法达到了他的目的！这真是不可思议的事！你猜得到，那神奇的1平方英尺究竟跑到哪儿去了吗？

● 教学反思

本课受欢迎程度如何？从课堂气氛的热烈和下课后的情景就可以深刻感受到。下课铃响了，学生仍然意犹未尽，汇聚成小组对感兴趣的问题热烈地进行探讨，迟迟不愿离去。可见，我的这次创意尝试获得了成功。整节课我和学生一起分享着我对“斐波那契”的狂想，让学生在轻松活跃的思维畅游中，享受数学美、算法美、自然美、艺术美、生活美……看起来我似乎是在进行美的熏陶，其实，我的真正目的并非仅局限于此。因为我发现迫于高考压力，不少高中生都在“死读书”，对知识点死记硬背，这样学习真的很苦、缺乏乐趣。就拿“斐波那契数列”来说，它本身是高中数学的一个知识点，很多学生都点到为止，会解数学题就可以了，但它背后所蕴含的巨大“宝藏”却很少被学生问津。如果像这堂课一样，运用发散思维，以这个知识点为圆心向四周扩展，学生在一系列的探索当中学到了很多领域的知识，而且逐渐学会运用所学的“知识点”揭示许多奥秘，提高生活、工作效率，懂得用知识来欣赏艺术、享受生活，这才是学习的真正意义。其实，这种方法不仅仅局限于数学，其他学科的学习也可以如此。所以，本课的最终目标是让学生把所学知识的最大价值发挥出来。