如何提高大学生的学习兴趣

石绍炳

摘要：在经过十二年的考试，最终进入大学，在这一阶段性目的实现后，学生不知道接下来该做什么。因为没有了学习的目的，也就没有了学习动力，没有了学习动力，也就没有了学习兴趣，因此如何提高大学生的学习兴趣对大学老师来说是一个不小的挑战。本文以实际教学为例，阐明了提出与学生紧密相联的、让学生感兴趣的问题，并让学生实际参与到教学中来，不失为提高大学生学习兴趣的好方法。

关键词：大学生；学习兴趣

在经过十二年的考试，最终进入到大学这一相对较宽松的环境后，在没有家长、老师为考分而逼迫的书本、试卷后，在学习的阶段性目的实现后，学生不知道接下来该做什么。因为没有了学习的目的，也就没有了学习动力，没有了学习动力，也就没有了学习兴趣，因此，正如爱因斯坦在追念居里夫人时曾说，科学家的科学精神、道德品质比其智慧结晶对当代和历史进程也许有更重大的意义，我始终坚信，每一位教育工作者（包括家长）最主要任务之一，与其说是传授具体的知识，勿宁说在于如何提高学生的学习兴趣，大学教师尤其如此。

1重建学生学习目的

下面是我给学生上第一堂课时经常的情景，我问学生：“你们为什么要上大学？”学生们先是有些愕然，然后大多回答：“拿个大学文凭，然后找个好工作，多赚点钱。”“那么凭什么找个好工作？”学生们又有些惶然，因为他们知道毕业时他们手中拿的文凭比不上北大清华，比不上名牌学校，而凭个人魅力，似乎又没有那份自信。“那么凭什么多赚点钱呢？”“凭……？……”“你们有自己感兴趣，而且以后想以自己的兴趣作为自己的职业吗？”“？？？”“那么为什么不好好思考一下自己对什么感兴趣，以后究竟想以什么为职业呢！”“……”。我们难以为每个学生确定学习目的，但我们可以引导他们确定他们自己的目的。不要说在专业课堂上说这些是浪费时间，引导学生在正确的道路上行走是每一个老师每时每刻的责任。

2如何提高学生的学习兴趣

如何提高学生的学习兴趣？这是一个见仁见智的问题，我下面以《统计分析软件》这门课程为例来阐述我的方法。很多人认为统计就是一大堆索然无味的数据、抽象、枯燥公式，如何提高学生的学习兴趣呢？费孝通先生曾将我国传统乡土社会比喻为“一块石头丢在水面上所发生的一圈圈推出去的波纹，每个人都是他社会影响所推出去的圈子的中心。”由“己”这个核心延伸开去，就像石子周围发生的涟漪一样，社会关系的展开和交易活动的进行，只是这个“己”的扩展而已……西方人的七个需求层次理论，也都是以“己”为中心展开的。基于这些“人总是对与自己有关的东西更感兴趣”这一普遍人性假设，因此，为提高他们的兴趣，让学生参与到制造一些与他们自己有关的数据的过程中来，并以这些数据为基础来进行分析不失为一个好办法。而且在多年的教学中，我真实地感受到：在教学的任何一个环节，让学生实际参与进来，更能发挥学生的主观能动性，更能激起学生的学习兴趣。

在讲授统计分析软件中时，先提出一个同学们普遍关心的问题，然后由同学们搜集或回答要解决这一问题的数据，后面以他们自己提供的数据作为分析数据。这样既避免学生在枯燥与乏味中学习软件操作，有利于提高学生的学习兴趣，又有利于提高学生解决实际问题的能力。例如，在讲解假设检验的这一实验时，先给出这样的一个问题：毕业后学生的期望收入是多少？五年后期望收入是多少？期望收入在不同的性别间是否存在差异？期望收入与学习成绩之间是否存在相关关系？根据问题的需要，建立了四个指标：毕业后第一年的期望月收入、毕业后第五年期望月收入、性别以及自己的学习（以优良中差四个等级作为变量值，越大表示成绩越好），其中学习成绩数据供以后的方差分析及相关分析用。然后将这四个指标变量在一张EXCEL表上制作好让学生从教师机上下载，由同学自己对未来的预期进行匿名填报，然后由老师通过统计软件把这些已填有每个学生数据的EXCEL表格进行自动串接，生成可供分析的数据表。数据搜集完成以后，给学生15分钟左右的时间思考应如何进行分析，同时提醒学生要注意各种统计方法的使用条件。

15分钟之后，根据解决问题的思路开始本次分析软件的讲解。下面是以其中一个班的数据展开的分析。

从上面的表和图可以看出，学生毕业后第1年的期望收入的均值是1642.86元，对于问题中的“期望收入在不同的性别间是否存在差异”应用两独立样本的T检验方法来进行分析，两独立样本的T检验是对两个独立正态总体的均值进行检验，在应用这一统计分析方法之前，应根据不同性别分别检验取得这两个样本的总体是否服从（或近似服从正态分布）。以事先给定的显著性水平5%，发现女生第5年期望收入的不近似服从正态分布，因此不能对原数据进行T检验。然而可以对数据进行对数变换并重新检验，结果如表2，结果表明可以以等方差的两独立样本T检验进行分析

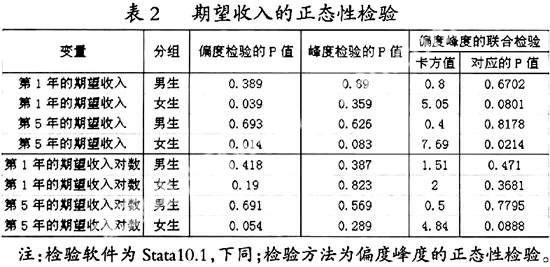
由于T 检验需要知道两总体的方差是否相等，因而还需对方差进行检验，检验结果如表3所示。

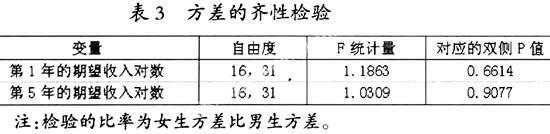
在5%的显著水平下，表3的检验表明，此数据并不能给出拒绝男生与女生在第1年的期望收入对数，还是在第5年的期望收入对数上的方差相等的假设，因而可以对这两个期望收入的对数进行T检验，检验结果如下表4。

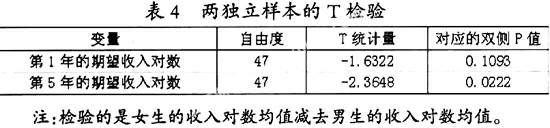
以5%的显著水平，根据表4的检验结果可以发现，男生与女生对毕业后第5年的期望收入存在一定的差异，但并不发现男女生在第1年的期望收入上存在差异的证据。

对于期望收入之间、期望收入与学习成绩之间是否存在相关关系应采用相关分析。由于两个期望收入都是连续变量，在不区分性别的情况下不能拒绝来自正态总体的假设，因此可以通过计算Pearson相关系数，然而由于学习成绩是以优良中差四个等级作为变量值的分类变量，因而以Pearson相关系数来分析是不恰当的，而应用Spearman等级相关系数或者是Kendal秩相关系数。检验发现两个期望收入的Pearson相关系数为0.8877，相应的伴随概率为0.0000，因此在5%的显著水平下可以认为第1年的期望收入与第5年的期望收入之间存在显著的正相关关系。学习成绩与第1年期望收入以及和第5年期望收入的Spearman等级相关系数分别为0.3212和0.3006，相应的伴随概率分别为0.0244和0.0359，因此在5%的显著水平下，可以认为两个期望收入都与学习成绩相关。得到的结论是：1、工作第一年的期望工资与性别没有关系；2、工作五年后男性期望工资比女性要高；3、期望工资与学生成绩排名呈正向关系。

3引导学生体验学习成功的喜悦，进一步激发学习动机

苏霍姆林斯基曾经说：“在学习中取得成功，是学生精神力量的唯一源泉，它能产生克服困难的动力，激发学习愿望。”一方面，在课堂教学中对教师提出的问题，学生经过自己的艰苦思考，一旦找到正确答案，教师就应及时给予肯定的评价，如点头示意，微笑，或用简短的语句加以称赞、鼓励等。在学生的作业或笔试后，可根据学生的学习态度、情绪、习惯适时进行正面评价，让学生感受成功的愉悦，这不仅可以使学生形成进一步努为学习的强大动力，而且还有利于学生心理健康发展。对学得特别好的学生可用激励性的批语；对学习上有进步的学生可用一些鼓励性的语言。这样，在老师的帮助下，既能让学生在各自不同的起跑线上逐步发展自我，完善自我。又能激发学生进一步学习的愿望，自我肯定的学习动力。另一方面，大学生不再满足于动手做做题，或动动实验室的设备，他们更希望解决实际的问题，因此，在布置课后作业时，可以布置一些与现实有联系的题目，如有一次，我给学生布置的题目是：大学英语四六级通过率的影响因素，要求以他们自己调查的数据为基础来分析。总之，在教学过程中，教师要创造条件，让每个学生都有充分表现自己的机会。每当学生学习获得成功后都应让他们体会成功的喜悦，以此保证学生自始自终都积极主动地参与到学习中来。

参考文献：

[1]张小红.当代大学生学习动机现状与原因分析[J].成都信息工程学院学报.

[2]赵志红.大学生学习动机的调查与培养[J].山西农业大学学报(社会科学版).

[3]杜兆君.重视研究生学习动机的培养[J].高等理科教育,2004,(06).

[4]何飞龙.从择业观论大学生主体意识的培养[J].广西高教研究,2002,(03).

[5]王天夫,李博柏.stata实用教程［M］.北京：中国人民大学出版社，2008. [6]劳伦斯.汉密尔顿著，郭志刚等译.应用stata做统计分析［M］.重庆：重庆大学出版社，1994.