债券法定计息期与会计计息期不同时实际利率法核算的Ｅｘｃｅｌ实现

张亚杰　朱学义

［摘 要］ 债券法定计息期与会计计息期不一致时，实际利率的计算以及利息调整的摊销比较复杂。本文通过剖析实际利率原理，结合具体案例，列出正确的实际利率计算公式及合理的摊销方法，运用Excel函数工具设计实现方案，准确方便可行。

［关键词］ 法定计息期；会计计息期；实际利率法；Excel

［中图分类号］F232［文献标识码］A［文章编号］1673-0194（2009）04-0007-03

新会计准则规定，划归为“持有至到期投资”的债券投资，应当采用实际利率法，按摊余成本计量。对于债券法定计息期与会计计息期不一致时的实际利率法核算，由于计息期限的不均等，如果购买日与发行日也不同，则实际利率的计算以及利息调整的摊销将更为复杂。本文从剖析实际利率的原理出发，运用Excel函数工具，结合具体案例做一下分析处理。

一、实际利率原理剖析

新会计准则规定：实际利率，是指金融资产或金融负债在预期存续期间或适用的更短期间内的未来现金流量，折现为该金融资产或金融负债当前账面价值所使用的利率。

1． 实际利率是复利含义，且按法定计息期进行“利滚利”

从财务视角分析，债券投资的实际利率实质就是投资人的实际报酬率，且是一个复利的概念。如债券按年付息一次，到期还本，其等价于：分期利息不取走到期再取息的话，利息是按年实际利率水平“利滚利”的；如债券按半年付息一次，到期还本，其等价于：分期利息不取走到期再取息的话，利息是按半年实际利率水平“利滚利”的；按季（月）付息同理。如债券是到期一次还本付息，其等价于按年实际利率水平“利滚利”。所以，实际利率是一个复利的含义，相当于按债券的法定计息期进行“利滚利”。那么对于小于法定计息期的时期计息时，则应按实际利率水平单利算息，如再按复利算息，则“利滚利”的期限及次数与实际情况不符。

2． 计算实际利率需用未来实际时点的现金流量折现

从财务视角分析，将未来实际时点的现金流量折现为初始投资成本的利率才是投资人的实际报酬率即实际利率。

二、案例分析

甲公司2007年12月15日购入A公司同年10月1日发行的3年期债券，面值100 000元，购入价格为

102 017元（其中包含未到付息期的两个月利息1 000元），债券票面利率为6％，每年9月 30日和 3月 31日付息。对该债券企业将持有到期，获取利息收益。甲公司2007年12月15日购入债券时编制以下会计分录：

借：持有至到期投资——成本 100 000

持有至到期投资——利息调整 2 017

贷：银行存款 102 017

本例债券每年9月30日和3月31日付息一次，法定计息期为6个月，法定计息期数为6次，每个法定计息期末实收利息3 000元，到期收本100 000元，期初投资现金流出102 017元，共7个时点的实际现金流量。债券法定计息期间跨跃会计年度，按准则规定，在资产负债表日（本例只取年末）也应计算利息及摊销，共有3个会计计息期，但会计计息期只是计算利息，未产生实际的现金流量。

实际利率应是将未来实际时点的现金流量折现为初始投资成本的利率。本例实际的未来现金流量见表1。根据前述实际利率计算原理，对法定计息期计息时，按实际利率水平复利算息，对小于法定计息期的时期计息时，按实际利率水平单利算息。本例0期到1期可算4个月（因购买价款已含前两个月利息），应单利计息，以后各期均为法定计息期，按复利计息。设半年的实际利率为r，可列出以下等式，利用Excel函数工具，可求出实际利率。

[3 000×P/A（r，5） +100 000×P/F（r， 5） +3 000 ] / （1+4× r/6） ＝102 017 （公式1）

或者：[3 000×P/A（r， 6） +100 000×P/F（r， 6）] /（1+2× r/6） ＝102 017

或者：[3 000×F/A（r， 5） +100 000+3 000] ＝102 017 （1+4× r/6） × F/P（r， 5）。

利息调整摊销时要点如下：

（1）摊余成本的计算

分期付息的债券摊余成本＝期初摊余成本＋实际利率计算的投资收益-应收利息

＝期初摊余成本×（1＋实际利率）-债券面值×票面利率；

一次还本付息的债券摊余成本＝期初摊余成本＋实际利率计算的投资收益

＝期初摊余成本×（1＋实际利率）。

（2）投资收益的计算

一般情况下，本期投资收益=期初摊余成本×实际利率。但对于小于债券法定计息期的期间计息时，应按实际利率水平单利计算。

（3）应收利息的计算

应收利息＝债券面值×票面利率。

三、案例的Excel实现方案

1． 计算实际利率

由于债券法定计息期为半年，设半年的实际利率为r。实际利率测算过程见图1，采用逐步逼近法测算。

具体步骤如下：

第一步，在对应单元格中输入各时点的现金流量，一般现金流入取正数，现金流出取负数。

第二步，在D6单元格中任意输入一个利率数据。

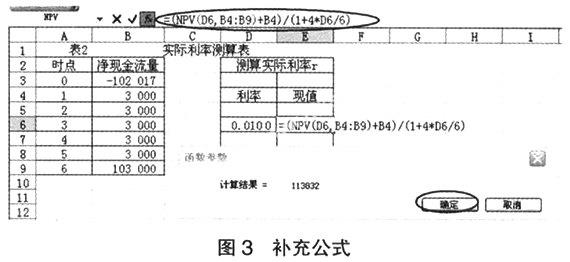
第三步，在E6单元格中输入现值计算公式，但不是简单地将上述6 个时点的数据折现等于0点的102 017。因为0~1点间隔4个月，1~6点均匀间隔6个月，实际利率r是按半年法定期限计复利，因此根据公式１：［３ ０００×Ｐ／Ａ（ｒ，５） ＋１００ ０００×Ｐ／Ｆ（ｒ， ５） ＋３ ０００］／ （１＋４× ｒ／6）=102 017，E6公式应设计为：2~6时点的数据折现到时点1（可用NPV函数）再与原时点1的数据相加，之后对相加的总和再折现4个月至0时点，让其等于0时点的102 017，这个折现率就是所求的实际利率。

①选中E6单元格，点插入（函数）或fx，选NPV函数，在rate项选入D6单元，在Value1项选B4至B9单元，不要点确定（见图2）。

②将光标调至公式栏，将公式补充完整，最终为“=（NPV（D6，B4:B9）+B4）/（1+4*D6/6）”，点确定（见图3）。

第四步，不断调整D6单元格中的数据，如现值计算结果大于初始投资成本102 017，则调高D6单元格中的数据；如现值计算结果小于初始投资成本102 017，则调低D6单元格中的数据，直至计算结果正好等于初始投资成本102 017，所对应的贴现率即为实际利率。本例实际利率r =2.8%。

2． 利息调整摊销

求出实际利率后，编制利息调整摊销表（见图4）。

具体步骤如下：

第一步，设计表式，输入初始数据。

①在各计息日对应单元格输入计息月数；

②在实际利率对应单元格F1输入实际利率2.8%；

③在单元格F4输入初始摊余成本即初始投资成本102 017；

④在单元格C5输入3个月的利息1 500（虽计息月数为1，因为12月15日购买时含未到付息期的2个月利息，年末算应收利息应含3个月，无法设通用公式）。

第二步，在单元格C6输入应收利息公式：100 000*

B6*6%/12，点单元格C6填充柄，拖曳至C13，各期利息即计算出来。

第三步，在单元格D5输入投资收益公式：=ROUND（F4*$F$1/6*B5，0）。

①注意实际利率要取绝对地址（$F$1），否则拖曳公式时会同步变化；

②同时要做整数位取整（ROUND）处理，否则系统有时可能会出现不平衡结果；

③一般情况下，本期投资收益=期初摊余成本×实际利率。但对于小于债券法定计息期的期间计息时，应按实际利率水平单利计算。如第0年12月31日，计息期为1个月，投资收益=期初摊余成本×实际利率=102 017×1×2.8%/6=476（元），本期末摊余成本=102 017+476-1 500=100 993（元）。接着第1年3月31日，计息期为3个月，小于法定计息期6个月，其投资收益仍需用第0年12月31日的期初摊余成本102 017元来计算，即投资收益=上期期初摊余成本×实际利率=102 017×3×2.8%/6=1 428（元）。此处如用本期期初摊余成本100 993元来计算，则对前1个月的利息又计息了，是按3个月“利滚利”了，与实际的按法定计息期6个月计复利相悖，会出现不平衡的结果。

因此投资收益公式应分两种：对每年的3月31日应用上期期初摊余成本计算，其他则用本期期初摊余成本计算。

第四步，在单元格E5输入利息调整公式：= C5-D5。

第五步，在单元格F5输入摊余成本公式：=F4+D5-C5。

第六步，将公式D5-F5，拖曳至最后计算期的前一期，再对每年的3月31日的投资收益公式做微调，改用上期期初摊余成本计算。

第七步，对最后一期做利息调整，因存在小数尾差，应做倒挤处理，单元格E13公式：=F12-100 000，单元格D13公式：=C13-E13。

至此，公式设置完毕，相关数据可随时算出。该方法准确，方便可行。