解决问题策略的教学实践与思考
章 莉
《数学课程标准》对“解决问题的策略”提出了明确要求:形成解决问题的一些基本策略,体验解决问题策略的多样性,发展实践能力和创新精神。教师在教学中应科学合理地制定教学目标,激发学生学习策略的动机,关注策略的形成过程、策略的价值、策略背后的思想,而不是把策略当成结论性知识或程序性技能传授给学生。
一、让学生产生学习策略的需求
教学时注意创设情境,唤醒已有的知识、经验,制造认知冲突,能激发学生主动寻求解决问题策略的热情。
情境1育华实验小学要举行乒乓球比赛,有15名选手参加。如果每2名选手间进行一场比赛,一共要赛多少场?
学生开始都会根据以前的学习经验,尝试运用画图的策略来解决情境中的问题。但是在探究过程中学生感到运用画图策略来解决比较麻烦。
教师创设参赛选手人数较多的情境,让学生感受解决问题的复杂性,一方面可以引发学生积极思考,产生从简单人手策略的强烈心理需求;另一方面可以促使学生初步认识从简单人手策略的内涵,即它是一种迂回策略,而不是从简单到复杂的循序渐进。
二、让学生经历策略的形成过程
解决问题的策略不同于解决问题的方法。方法可以在传递过程中习得,但策略只能在方法的实施中感悟获得。教师要准确定位策略教学的目标,让学生体验策略的形成过程,并从中获得对策略内涵的认识与理解。
(一)潜意识阶段
上述情境中的问题,教师可引导学生进行下列学习活动:
1引导:这个问题比较复杂,可先从最简单的情况人手,看看其中有没有规律。
2思考:①从多少人比赛开始研究?②当比赛人数一定时,怎样有顺序、有规律地呈现选手间的比赛情况?③比赛场数与参赛人数之间有怎样的联系?
3学生分组活动。
4全班交流,展示典型方案。
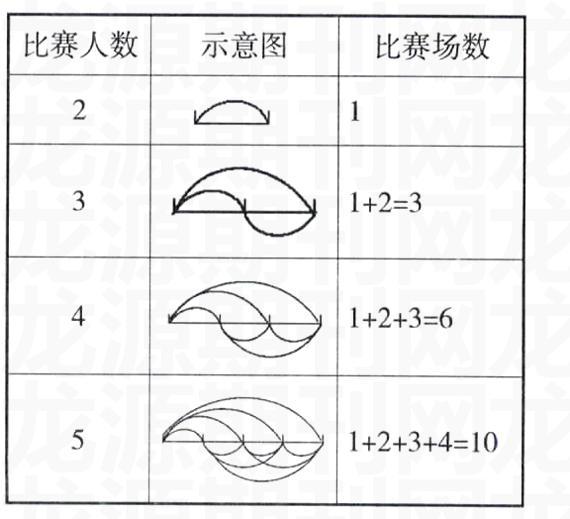
5讨论:随着比赛人数的增加,比赛场数是怎样变化的,其中有什么规律?
6,应用规律:15名同学参加比赛,一共要比赛多少场?怎样列式?
7回顾:解决15人的比赛场数问题时是怎样思考的?(从简单情形人手)
8反思:为什么要运用从简单人手策略?运用从简单入手策略解决问题时一般是怎样做的?
学生在丰富多样的数学活动中经历了“遇到复杂问题一解决同类简单问题一探究解决简单问题时的规律一应用规律解决较复杂问题”的过程,初步体验到从简单人手策略的形成过程。
(二)明朗化阶段
情境2有一个生日蛋糕,只准垂直向下切,不准水平横切,10刀最多能将一块圆形蛋糕切成多少块?
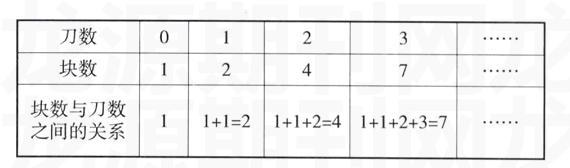
新问题呈现后,组织学生思考可以用什么策略解决,使学生具有明确的应用策略的意识。学生都会自觉运用从简单人手策略,通过画图寻求答案。为了便于发现其中的规律,教师引导学生从切O刀的情况画起,并列表整理答案。(表格见P49)
引导观察:从第2列开始,每一列与前一列比较,切几刀,最多能切出的块数就是在前一列块数的基础上多几。学生根据块数与刀数之间的变化规律顺利解决新问题。
问题解决后,再组织学生交流解决问题的过程。这样,随着解决问题策略的初步应用,学生对从简单人手策略的认识开始明朗化。
(三)深刻化阶段
解决比赛场数及切蛋糕块数问题都是从简单人手,借助画图或列表策略,从中发现规律,进而解决问题的。为了防止学生思维定势,认为运用从简单人手策略解决问题就要借助画图或列表策略,教师可再设计其他的拓展练习。情境31/(1998+1999)+1/(1999+2000)+1/(2000+2001)+……+1/(2008+2009)
解决这个问题也可从简单人手,先研究1/(1×2)+1/(2×3)+1/(3×4)+1/(4×5)中的计算技巧,再推广到原问题去解决。在这一解题过程中,尽管也是运用从简单人手策略,但没有依靠画图或列表策略。而是渗透了猜想—举例—验证的策略。之后,教师要引导学生反思运用从简单人手策略的解题过程,使学生对策略的本质有更深入的认识,促进学生形成稳定的解决问题的策略。同时,学生在不断整合、应用不同策略解决问 题的过程中,体验解决问题策略的多样性,培养了学生面临新问题灵活运用各种策略解决问题的意识。
三、让学生体验策略的应用价值
解决问题策略的价值不仅仅是解决某一类问题,获得某一类问题的结论,更重要的是在解决问题的过程中基于解题的经历,形成相应的经验、技巧、方法,进而通过反思和提炼,对策略本身有更深刻的理解,形成解决问题的基本策略,并体会策略的价值。
教师可这样引导学生回顾反思:为什么要使用从简单人手策略?使用该策略有什么好处?在什么情况下使用该策略?学生在自我内化的过程中感受策略给解决问题带来的便利,体会策略的价值,增强运用策略解决问题的自觉性。
四、让学生感悟策略背后的数学思想
数学学习的核心在于数学思想方法的建立。教师要通过策略的教学,帮助学生不断积累数学活动经验,感悟策略背后的数学思想。
学习问题1、2、3之后,教师应引导学生将实际问题抽象成数学模型。可设计这样的提问:①当参赛队员为n名时,一共要比赛多少场?②当切n刀时,最多可切多少块?③当从1/(1×2)+1/(2×3)+1/(3×4)+……一直加到1/(n×(n×1))时,怎样计算?学生通过抽象化、符号化,构建相应的数学模型为:①比赛场次是(n×(n-1))/2;②最多切的块数是(n×(n+1))/2+1;③计算方法是: 1-1/(n+1)=n/(n+1)。
学生从简单人手发现规律,构建数学模型的过程也是一个归纳推理的过程。教师要使学生通过策略的运用,模型的建立,感悟从简单人手策略背后的数学思想——归纳推理思想,从而提升学生的数学思维能力,培养学生的数学素养。
(责编林剑)

