例谈“最短路线”与“相等路线”的作法
韩永华
最短路线与相等路线的作图来源于生产、生活的实践,是落实《数学课程标准》的重要资源,其作图方法和理论依据对国家的经济建设具有重要的指导意义.指导学生解决这类实际问题,能够实现大量知识的有效整合,达到举一反三、触类旁通的目的.现从以下两个方面的具体实例说明这类问题的作图方法及其理由.1 与直线相关的作图
1.1 两个已知点在已知直线的同一侧
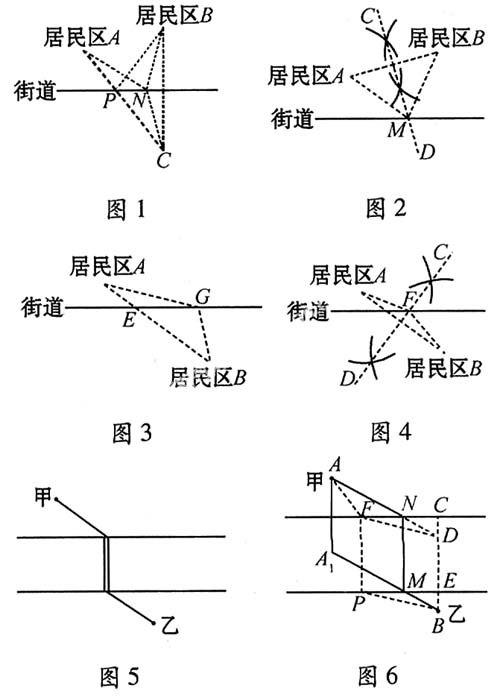
例1 如图1所示,要在街道旁修建一个奶站,向居民区A,B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短?
作法 (1)作点B关于街道的对你点C;
(2)连结AC交街道于点P.
故奶站应建在点P 处.
证明 在街道上任取一点N,连结AN、BN、CN、PB.
因为点B和点C关于街道对称,
所以PB=PC,BN= CN.
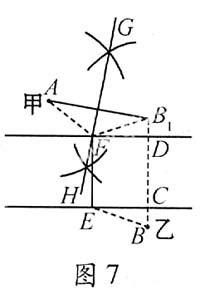
又因为AC 所以AP+PB 故奶站建在点P 处,A、B到它的距离之和最短. 例2 如图2所示,要在街道旁修建一个奶站,向居民区A,B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离相等? 作法 (1)连结AB; (2)作线段AB的垂直平分线CD,交街道于点M.故奶站应建在点M处. 证明 连结AM、BM. 因为点M在线段AB的垂直平分线上,所以AM=BM. 故奶站建在点M处,A、B到它的距离相等. 1.2 两个已知点在已知直线的两侧 例3 如图3所示,要在街道旁修建一个奶站,向居民区A,B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短? 作法 连结AB,交街道于点E. 故奶站应在点E 处. 证明 在街道上任取一点G,连结AG、BG. 因为AB 所以奶站建在点E处,A、B到它的距离之和最短. 例4 如图4所示,要在街道旁修建一个奶站,向居民区A,B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离相等? 作法 (1)连结AB; (2)作线段AB的垂直平分线CD,交街道于点F. 故奶站应在点F 处. 证明 连结AF、BF. 因为点F在线段AB的垂直平分线上, 所以AF=BF. 故奶站建在点F处,A、B到它的距离相等. 2 与街道的宽度相关的作图 例5 如图5,甲、乙两个单位分别位于一条封闭式街道的两旁,现准备合作修建一座过街的天桥.问: (1)桥建在何处才能使由甲到乙的路线最短?注意桥必须与街道垂直. (2)桥建在何处才能使甲、乙到桥的距离相等? 解 (1)如图6,将点A向垂直于街道的方向平移到点A1,平移的距离为街道的宽度,连结A1B交街道的边缘于点M,所以桥应建在MN处(MN与街道垂直),就能使由甲到乙的路程AN+NM+MB最短. 证明 假设桥建在不同于MN的任意一处FP(FP与街道垂直),过点B作与街道垂直的直线BC与街道边缘的垂足分别为C、E,延长AN交BC于点D,连结AF、PB、FD. 因为AA1=MN,AA1∥MN,所以四边形A1MNA为平行四边形.所以AN=A1M,ND∥MB.又因为MN∥BD,所以四边形MBDN为平行四边形.所以MB=ND.易证四边形MECN为矩形.所以ME=NC.所以△MBE≌△NDC. 所以BE=DC.易证四边形PECF为矩形.所以PE=FC.所以△PBE≌△FDC.所以PB=DF.因为AD 故桥建在MN处,由甲到乙的路线最短. (2)如图7,作点B关于街道的对称点B1,B1B与街道边缘分别交于点C、D.连结AB1,作线段AB1的垂直平分线交街道的边缘于点F,所以桥建在FE(FE与街道垂直)处,就能使甲、乙到桥的距离相等. 证明 连结AF、B1F、BE. 因为点F在线段AB1的垂直平分线上,所以AF=B1F.易证四边形ECDF为矩形.所以EC=FD.又因为B和B1关于街道对称,所以BC=B1D.所以△BCE≌△B1DF.所以BE=B1F.所以AF=BE. 故桥建在FE处,甲、乙到桥的距离相等. 以上实例的解答过程共用到了以下12个方面的数学知识:(1)作已知点的轴对称点的方法;(2)轴对称的性质;(3)三角形三边的关系;(4)作线段中垂线的方法;(5)线段中垂线的性质;(6)平移一个点的方法;(7)平行四边形的判定;(8)平行四边形的性质;(9)矩形的判定方法;(10)矩形的性质;(11)全等三角形的判定方法;(12)全等三角形的性质.显然,像这样的题组式的教学不仅让学生体验到了变式给他们带来的乐趣和挑战,同时大量的数学知识得到了运用与巩固. プ髡呒蚪榧本刊2008年第10期(总第222期第58页).