与垂直平分线有关的计算题

邓　凯

与垂直平分线有关的计算题主要有两类，一类是关于边长和周长的计算，一类是关于角的计算．要熟练解决与垂直平分线有关的计算题，关键是要掌握垂直平分线的性质以及有关的结论．

如图1所示，在△ABC中，DE是BC边上的垂直平分线，有以下结论（根据垂直平分线的性质很容易证明）.

1．关于边长和周长的结论：

（1）BE=CE；（2）BD=CD=1/2BC；（3）AB=AE+CE；（4）△AEC的周长=AC+AB；（5）△ABC的周长=△AEC的周长+BC．

2．关于角的结论：

（1）∠BED=∠CED；（2）∠B=∠BCE=1/2∠AEC．

一、关于边长和周长的计算题举例

例1如图2，在△ABC中，AC的垂直平分线交BC于E，交AC于D.△ABE的周长是16 cm，AC=6 cm.（1）求AB+BE+EC的长度；（2）求△ABC的周长．

解析：（1）因DE是AC的垂直平分线，故AE=CE.

∵△ABE的周长是16 cm，

∴AB+BE+EC=AB+BE+AE=16（cm）.

（2）由（1）的结论及AC=6 cm，可求得△ABC的周长=AB+BE+EC+AC=22（cm）.

点评：这是一道与垂直平分线有关的经典题．解题时，需要运用AE=CE这一结论．与此题类似，还可以作出边AB、BC的垂直平分线，并设计出类似的问题．

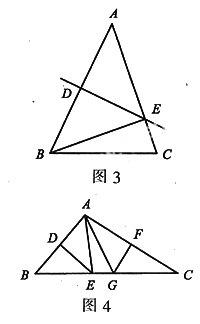
例2如图3，在△ABC中， AB的垂直平分线交AB于点D，交AC于点E.△BCE的周长等于16 cm.（1）若BC=7 cm，求AC的长；（2）若AC的长为9.6 cm，求BC的长．

解析：（1）∵DE是AB的垂直平分线，

∴AE=BE.

∴AC=AE+EC=BE+EC=16-7=9（cm）．

（2）由（1）可知BC=16-9.6=6.4（cm）.

点评：这道题的两个小题，解决思路是“互逆”的，但所用的基本结论是一样的．

与垂直平分线相关的边长和周长的计算题，往往只涉及垂直平分线的性质的基本应用，一般运用上述结论即可解决．

练习

1. 如图3，△ABC中，AB的垂直平分线分别交AB、AC于D、E.如果AC=5 cm，BC=4 cm，则△BEC的周长是（）.

A． 9 cm B． 13 cm C． 14 cm D． 13 cm或14 cm

2. 如图3，在△ABC中，已知AC=27.AB的垂直平分线交AB于点D，交AC于点E.△BEC的周长等于40.求BC的长.

二、关于角的计算题举例

例3如图4，在△ABC中，DE、FG分别是边AB、AC的垂直平分线.（1）试分别写出与∠B、∠C相等的角；（2）若∠BAC=100°，则∠EAG等于多少？

解析：（1）∵DE、FG分别是边AB、AC的垂直平分线，

∴AE=BE，AG=CG.

∴∠B=∠BAE，∠C=∠CAG.

（2）由（1）可知，∠EAG=∠BAC-（∠BAE+∠CAG）=∠BAC-（∠B+∠C）=100°-（180°-100°）=20°.

点评：这是一道典型的与垂直平分线有关的角的计算题.与上面边长和周长的计算题一样，关于角的计算题，依然涉及垂直平分线的性质的应用，解题时需要运用到垂直平分线的性质中关于角的基本结论.

练习

3. 如图3，△ABC中，AB的垂直平分线分别交AB、AC于D、E.若∠BEC=100°，则∠A=______．

4. 在Rt△ABC中，∠C=90°，AC>BC.AB的垂直平分线与AC相交于E点，连接BE.若∠CBE∶∠EBA=1∶4，则∠A=_____，∠ABC=___.

三、综合题举例

例4如图5，在△ABC中， AB的垂直平分线分别交AB、BC于点D、E， AC的垂直平分线分别交AC、BC于点F、G. 且BC=12，∠BAC=120°.（1）求△AEG的周长；（2）求∠EAG的大小；（3） 若AB=AC，试判断△AEG的形状.

解析：（1）∵DE、FG分别是AB、AC的垂直平分线，

∴AE=BE，AG=CG.

∴△AEG的周长=BE+EG+CG=BC=12.

（2）∵DE、FG分别是AB、AC的垂直平分线，

∴∠B=∠BAE，∠C=∠CAG.

∴∠EAG=120°-（∠B+∠C）=120°-（180°-120°）=60°.

（3）由AB=AC，可得∠B=∠C=30°.

∴∠AEG=∠AGE=60°.

∴△AEG为等边三角形．

点评：这道题既有边长和周长的计算，也有角的计算，是一道与垂直平分线相关的综合计算题．其中涉及到的解题思路（如求∠EAG），在前面的例题中已有体现．

例5如图6，在Rt△ABC中，斜边AB的垂直平分线分别交AB、BC于点D、E．若BE=2，∠B =15°，求直角边AC的长．

解析：如图7，连接AE.

∵DE是AB的垂直平分线，

∴AE=BE=2，且∠AEC =2∠B=30°.

在Rt△AEC中，由“直角三角形30°角所对的直角边等于斜边的一半”，可求得AC=1.

点评：这道题相对于例4来说，不仅有与垂直平分线相关的计算，而且还有与其他数学知识的综合运用.

练习

5. 如图4，在△ABC中，DE、FG分别是边AB、AC的垂直平分线.若BC=a，请用含a的式子表示△AEG的周长.

6. 如图8，△ABC中， AB的垂直平分线分别交AB、BC于点D、E， AC的垂直平分线分别交AC、BC于点F、G.（1）若∠BAC =75°，求∠EAG的大小；（2）若BC=20，GE=8，求△AEG的周长.

7. 如图3，在△ABC中，AC=a，AB的垂直平分线DE交AC于点E.若△BCE的周长为m，求证：BC=m-a.

综上所述，与垂直平分线相关的计算题，基本题型变化不大.此时，只要牢牢把握住垂直平分线的性质和基本结论，就能顺利地解决问题.