点击“轴对称”

卢定波

一、基础知识精要

1. 轴对称、对称轴、对称点

把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么称这两个图形关于这条直线对称，也称这两个图形成轴对称.这条直线叫做对称轴.两个图形中的对 应点叫做对称点.

如图1，如果△ABC沿直线PQ折叠后，与△A′B′C′重合，则称△ABC与△A′B′C′关于直线PQ对称，直线PQ是对称轴，点A与A′、B与B′、C与C′是关于直线PQ的对称点.

提醒：（1）轴对称包含两层意思：①有两个图形，能够完全重合，即形状大小都相同；②对重合的方式有限制，也就是：把它们沿着某一条直线对折后能够重合.

（2）对称轴是一条直线，而非线段、射线等.

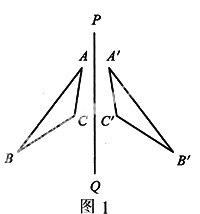
（3）对称点是指折叠后重合的点，对称线段也是指折叠后重合的线段，如图1中线段AB与A′B′就是关于直线PQ对称的线段.

2. 轴对称图形

把一个图形沿着某一条直线折叠，如果直线两旁的部分能够互相重合，那么称这个图形是轴对称图形，这条直线就是对称轴.

提醒：轴对称图形是指一个图形的本身.

3. 轴对称与轴对称图形的关系

它们的主要区别是：（1）轴对称是两个图形之间的对称关系，轴对称图形是一个图形自身的对称特征；（2）轴对称的对称点分别是在两个图形上，轴对称图形的对称点是在同一个图形上；（3）两个图形成轴对称，其对称轴可能在两个图形的外部，也可能经过两个图形的内部或它们的公共点（边），轴对称图形的对称轴一定经过这个图形的内部.

它们的主要联系是：

（1）都是沿某直线翻折后能够互相重合的.

（2）若把轴对称的两个图形看成一个整体，那么它就是一个轴对称图形；若把轴对称图形沿对称轴所在直线分成两部分，那么这两部分又可看成关于这条直线成轴对称.

4. 成轴对称的两个图形的性质

（1）成轴对称的两个图形全等.

（2）如果两个图形成轴对称，那么对称轴是对称点连线的垂直平分线.如图1，△ABC与△A′B′C′关于直线PQ对称，则△ABC≌△A′B′C′，PQ垂直平分线段AA′、BB′、CC′等.

（3）成轴对称的两个图形，如果对称线段（或其延长线）相交，那么交点在对称轴上.

提醒：（1）如果两个图形关于某直线成轴对称，那么这两个图形全等；反过来，两个图形全等，这两个图形不一定成轴对称（如一个三角形绕其某顶点旋转一定角度，所得的两个全等三角形）.

（2）若两个图形成轴对称，则连接对称点的线段被对称轴垂直平分.

5. 关于画图

如果一个图形是轴对称图形，那么连接对称点的线段的垂直平分线就是该图形的对称轴.

而画一个图形的轴对称图形时，要先确定对称轴，再找出对称点.找对称点时，关键是画出一些特殊点，如线段的端点、图形的顶点等.

二、典例剖析

例1如图2，下列图案中，是轴对称图形的是_______.

思维技巧：判断一个图形是不是轴对称图形，要抓住轴对称图形的特征，即对于这个图形来说，能够找到某条直线，沿着这条直线对折，对折的两部分能够完全重合.

解：由轴对称图形的特征可知，图中的（1）、（3）、（4）、（5）、（8）是轴对称图形.

点评：（1）一个图形是不是轴对称图形，是针对一个图形的整体而言的.图形的某一部分是轴对称图形不代表整个图形也是轴对称图形.（2）要善于变换角度去发现轴对称图形的对称轴，如例1的（8）.（3）防止视角差异导致误判.

例2试找出下列每个正多边形的对称轴的条数，并填入表格中.

根据上表，请就一个正多边形对称轴的条数作一个猜想.

思维技巧：先画出每一个正多边形的所有对称轴，分析对称轴的条数与正多边形的边数的关系，再通过几个正多边形验证，得出一般性的结论.

解：画出各正多边形的对称轴，其条数依次为3，4，5，6，8.由此可猜想：一个正n边形的对称轴的条数正好等于其边数n.

例3（1）如图4（1），已知点A、B和直线MN，试画出点A、B关于直线MN的对称点A′、B′.

（2）如图4（2），已知线段AB和直线MN，试画出线段AB关于直线MN的对称线段A′B′.

（3）如图4（3），已知△ABC和直线MN，试画出△ABC关于直线MN的对称图形△A′B′C′.

解：分别如图5中三个图所示.

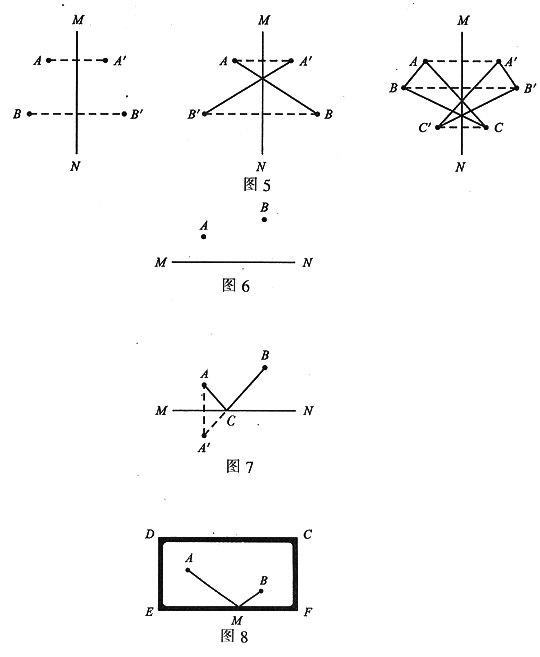
点评：当画某一复杂图形关于某直线对称的图形时，可以先画出它上面一些特殊的点关于直线的对称点，再依次连接即可得到结果.

例4（最短距离问题）如图6，直线MN表示一条小河.一牧民在点A放马，现在要让马到河边去饮水，然后回帐篷点B处（A、B在小河MN同旁）.问：饮水地在何处时才能使他所走的路最短？在图中表示出代表饮水地的点.

思维技巧：要使所走的路最短，即在直线MN上找到一点，使这个点到A和到B的距离之和最小.

解：如图7.画点A关于直线MN的对称点A′.连接A′B交MN于点C，点C就是所求的点.

点评：本例是利用轴对称性质解决实际问题的范例.作出B点关于MN的对称点B′，连接AB′，也能找出同样的C点.

例5（最佳点问题）设CDEF是一台球桌的矩形台面，A、B分别是黑、白两个球，如图8.如果击打黑球A，使黑球A碰到台球桌台边EF后反弹击中白球B，黑球A应经过怎样的路线？

思维技巧：如果A球击出后撞到台边EF上的M点反弹，恰好击中B球，设MN是垂直EF的直线，则有∠AMN=∠BMN.∠AMN、∠BMN分别称为入射角与反射角.大自然中，很多反射现象都遵循这个规律，例如光线从A处射入，经过镜面上一点M反射后，经过B点，也必有∠AMN=∠BMN.故作A点关于EF对称的点A′，连接A′B与EF相交于点M，击打黑球A到M点，即可使黑球A击中白球B.

探索与思考

1. 如图9，已知P为∠AOB内一点，请分别在OA、OB上作一点P′、P″，使△P P′P″周长最小.

2. 如图10，四边形ABCD是长方形弹子球台面.有黑、白两球分别位于E、F两点上.试问：怎样撞击黑球E，才能使黑球先碰撞台边CD，再撞击台边AD，反弹后击中白球F？