基于MATLAB仿真的多普勒中心估计算法改进研究

1 引 言

SAR作为现代雷达的一种，已经广泛应用于军事及国民经济等许多领域，如军事侦察、国土资源管理、环境监测等。多普勒中心频率fdc的估值是SAR信号处理中的关键步骤之一。在SAR成像处理中，fdc估值精确与否直接影响到SAR图像聚焦和运动补偿的精度。有很多学者就fdc估值问题提出了不同的算法[1-3]，频谱能量均衡法[4]是JOHN等人提出的一种fdc估计算法，也是应用较为广泛的一种，传统的能量均衡法在地面场景比较均匀的情况下能得到较好的估值精度，但当地面为非均匀场景时，尤其是场景中有非常强的点目标时，其估值性能急剧下降[5]，这种不足往往因多个距离门作平均处理而表现不明显，被忽略掉了；能量均衡法的另一个不足是其处理过程中含有迭代运算，很不适合DSP实时处理。文献[5-6]分别从不同的角度对频谱能量均衡法作了部分改进，文献[6]提到通过能量中心均衡逼近以及距离加权拟合来改进传统的能量均衡法；文献[5]则更多地考虑算法结果的精确性。本文从如何提高实时处理效率角度出发，通过更为简洁的算法避免了迭代运算，而且当回波中有强点目标时，通过删除异值的方法使估值结果更为准确，文章最后应用MATLAB语言进行了多普勒中心估计新算法的仿真，并给出了实际的成像应用成果。

2 SAR工作原理

SAR 的方位向和距离向的高分辨率都是通过对Chirp信号的压缩得到的，但是Chirp信号产生方式不同。雷达系统发射Chirp信号代替单频的雷达脉冲，并对接收到的回波信号进行脉冲压缩可以得到距离向的高分辨率。而在方位向上则利用了回波的方位相位调制，这种调制是由于在雷达运动过程中目标与雷达之间的距离随时间变化引起的。回波信号因多普勒效应而产生了近似于线性调频脉冲的信号，处理机将这一调制信号进行压缩，从而在宽波束天线上得到与窄波束天线相同的分辨率。为此，必须积累连续位置上的雷达回波才能进行SAR信号处理，这是其区别于其他成像雷达的主要特征，也是SAR技术的关键所在。

图1是载机和地面目标之间的基本几何关系。P为处于雷达波束照射下的点目标，图中参数φ为载机在O点(t=0)时向量OP与速度向量之间的夹角；h为载机飞行高度；v为载机速度；r为点目标P和载机的距离；rc为点目标P和载机的最短距离；R为载机在O点(t=0)时同点目标P之间的距离。

图1 载机与地面目标几何关系

根据图标的几何关系，雷达和点目标的距离函数为：

(1)

假设脉冲宽度为Tp，调频率为kr，雷达发射的脉冲线性调频信号的形式为：

(2)

则经过雷达波束照射区域内点目标P反射并去载频后，雷达接收到的回波信号为：

·

(3)

式中，Ta为合成孔径积累时间，c为光速，λ为工作波长。

对式(3)所示的回波信号的方位相位φ(t)=-4πr(t)/λ求导可以得到方位向瞬时频率：

fa(t)=fdc+frt|t|≤Ta/2

(4)

通常把它称为点目标回波的多普勒频率历史，简称多普勒历史。由其表达式可以看出，多普勒历史是一个按照负斜率变化的线性调频信号，其调频斜率(即方位向调频率)fr为：

(5)

多普勒中心频率为：

(6)

在SAR成像处理中，fdc估值的准确度非常重要，估值不准确将导致信噪比降低，方位模糊度增加，输出图像会发生位置偏移，影响SAR图像定位[7]。

3 频谱能量均衡法

由于点目标的SAR回波信号在方位向是线性调频信号，其瞬时频率和孔径时间存在线性关系。因此，在理想飞行情况下，方位向回波某个频率上的能量必然来自于雷达照射区域中某个特定方向上的目标。在假定照射区域为均匀场景(各点目标具有相同的散射特性和散射截面积)情况下，回波的方位向功率谱密度显然与雷达天线方向图有着相同的形状。通常情况下，天线方向图都是相对于波束中心对称的，因此，回波方位向功率谱密度也是对称的，其中心对称点即为多普勒中心。

由于点目标的方位谱是以多普勒中心频率fdc为中心对称，因而为方位谱的能量中心代替多普勒中心带来可能，这就是频谱能量均衡法。图2为该方法的流程图。

以下是传统的频谱能量均衡法具体操作步骤说明：

1) 根据SAR系统参数和惯导数据，得到多普勒中心频率的初值fDC;

2) 经过距离脉冲压缩处理，将回波信号转换到距离—多普勒域，产生方位谱信号；

3) 根据fDC将频谱搬移至零中频；

4) 计算零中频两侧方位谱的能量E1和E2；

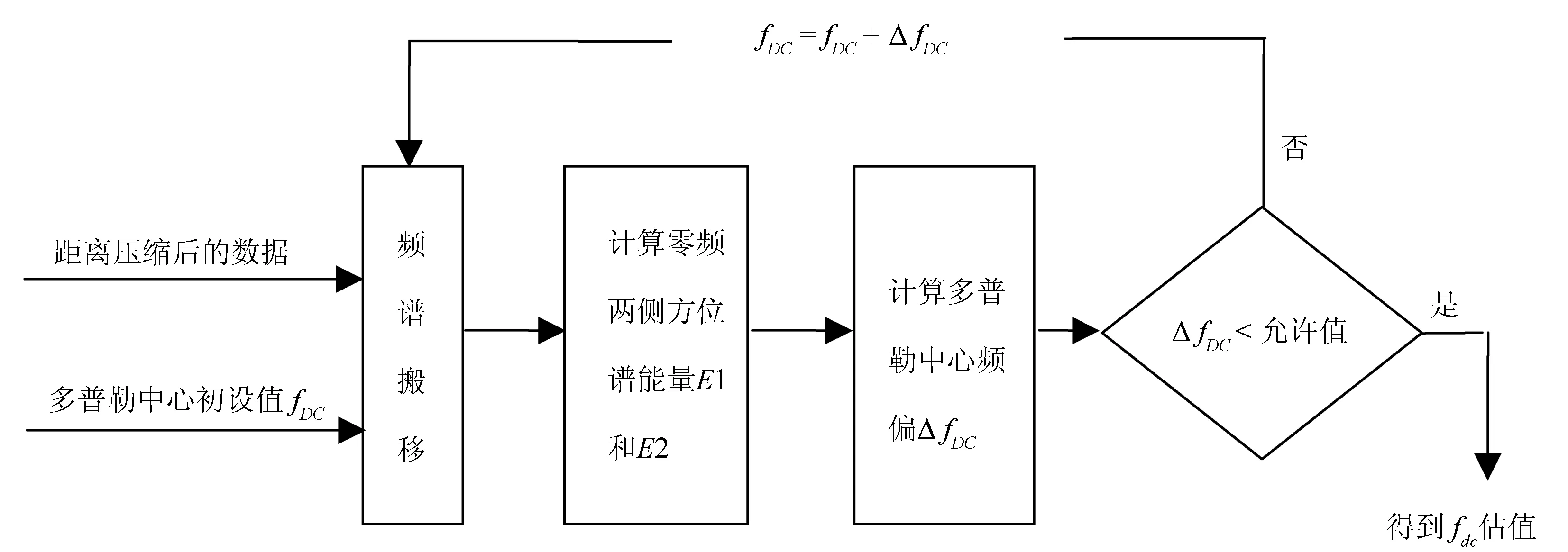
图2 频谱能量均衡法流程图

5) 计算此时的能量中心的估计值偏差ΔE=E1-E2;

6) 判断ΔE是否在允许的误差范围内，以便决定是否迭代，如果在允许误差范围内，则得到了fdc估值，否则fDC=fDC+ΔfDC并从步骤3)开始重复。

该方法由于存在迭代运算，因此不适合DSP实时处理，算法效率不高。

在实际应用中，当地面散射特性比较均匀时，回波谱对称性好，多普勒中心频率估计比较准确，但当场景不均匀时，尤其是存在强点目标时，该方法估值精度会下降很多。如图3所示，该图表现的是一段含有强点目标的方位向频谱，真实的多普勒中心应该在A点，但由于谱峰值B点处能量很强，如果用能量均衡法，则会将多普勒中心误判为B点或B点附近，使多普勒中心估计不准确，该点也就是我们所谓的频谱能量均衡法中需要注意的奇异点。若将频谱中该奇异点删除(如图4所示为将B点幅度赋零后的频谱图)，再通过能量均衡法估算fdc，就比较准确了。

图3 去异值前的频谱

图4 去异值后的频谱

4 能量均衡法的改进

上一节已经提到传统能量均衡法的一些不足，即存在迭代运算和在含强目标场景下估值不准的问题，新的方法主要在这两点上进行了改进。在频域上，对于强点目标回波，其幅度一定远远高于频谱能量均值，因此可以设定一个门限，将这些奇异值删去，即做赋零处理。

而对于迭代运算的简化处理，我们可这样考虑，在删除异值后，方位谱的包络大致近似于雷达天线方向图，能量中心点C′大约在频谱峰值点附近。我们可先找到峰值点，再通过加权处理的方式求得加权能量中心点C′的偏移量，这样就可得到加权能量中心点C′，当然这个C′并不等同于绝对的能量中心点C，但它是能量中心点C的一个估计值，而且估计误差较小，完全在容忍误差范围之内。在第5节中将列出由SAR原始数据处理得到的结果及其分析。

算法框图如下：

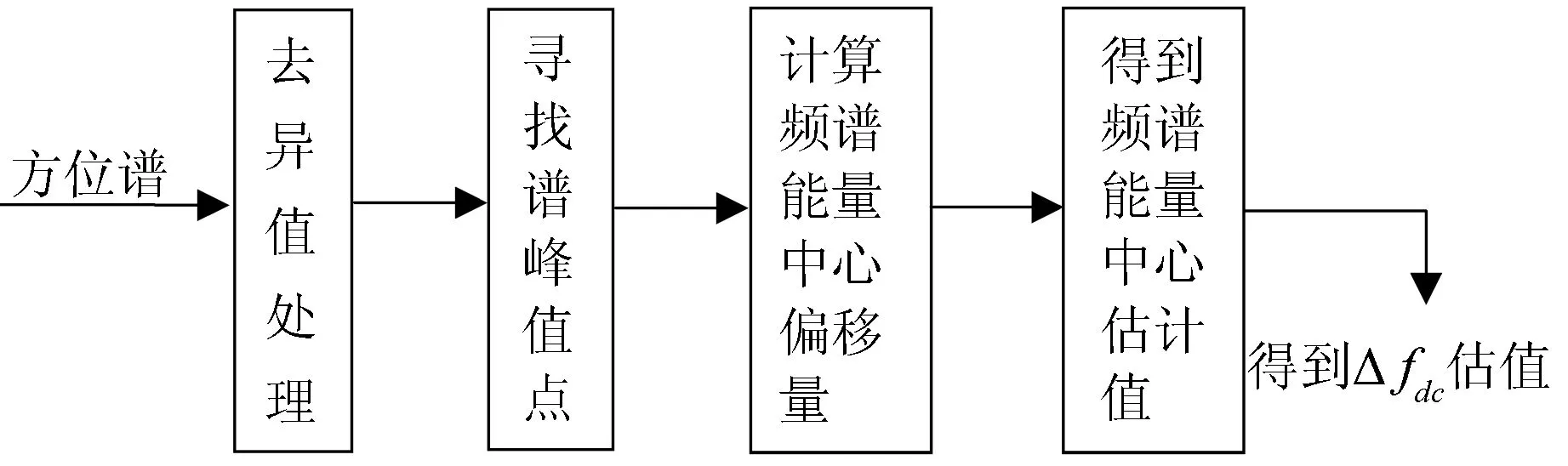
图5 改进的频谱能量均衡法流程图

以下是该算法具体操作步骤：

2) 寻找频谱峰值点p点，该频点幅度为A(p)；

4) 令第k频点加权值为g(k):

(7)

5) 求出加权频谱能量中心偏移量:

(8)

6) 求出频谱能量中心估计值C=p+Δf，该能量中心C所对应的频点值即为fdc估计值。

举例说明：当方位谱为128点傅立叶谱，首先删除掉异值点，得到删除了异值点后的谱，并找到这个新的谱的峰值点p点，假设p=110，即110频点。由公式(7)得到110频点加权值为0，109和111频点加权值分别对应-1、+1，依此类推，每个频点都对应着一个加权值g(k)(g(k)∈=[-63,64])，根据公式(8)得到加权频谱能量中心偏移量Δf，能量谱中心估计值为C=p+Δf，即fdc的估计值。

5 仿真实验及实测结果分析

5.1 仿真实验及结果分析

笔者通过MATLAB语言对该算法进行了仿真。首先构建了一个环境模型，环境参数如表1所示。

表1 仿真实验环境参数

雷达天线工作在扫描模式，因此不同的天线角度指向对应着不同的多普勒质心频率fdc，这种工作模式也非常适合分析验证fdc估值算法。

由参数可知，天线从72°～108°为半周扫描，共耗时2 s，即4 000个重频。我们对数据进行如下处理：首先在距离向做脉冲压缩处理；继而将方位向数据按128个重频划分作为一个相干处理单元CPI，则半周扫描(72°～108°)可划分为31.25个CPI，为方便计算，取32个CPI的数据处理，每一个CPI的数据在方位向做FFT相干积累后，用改进的能量均衡法估算fdc值(距离向每128个距离门做均值处理)。

图6(a)反映的是用新算法求解的连续32个解模糊之前的值，图6(b)反映的是解模糊之后的fdc值，图6(c)是环境模型中输入的天线扫描情况。通过比较图6(b)和图6(c)可看出天线来回扫描，从正速度到零速，再到负速度，32个fdc值求解得比较精确。

图6 天线扫描波束指向及对应的多普勒频率图

5.2 实测结果分析

我们选取某型雷达所测的一段实测数据，并选取均匀场景，一般非均匀场景2种类型数据，每一种场景数据考察3例，通过时域相关法、频谱能量均衡法和改进的频谱能量均衡法得到如表2、表3的对比结果(表2，表3中方法1表示时域相关法，方法2表示频谱能量均衡法，方法3表示改进的频谱能量均衡法)。

表2 均匀场景下各种fdc估值方法结果比较

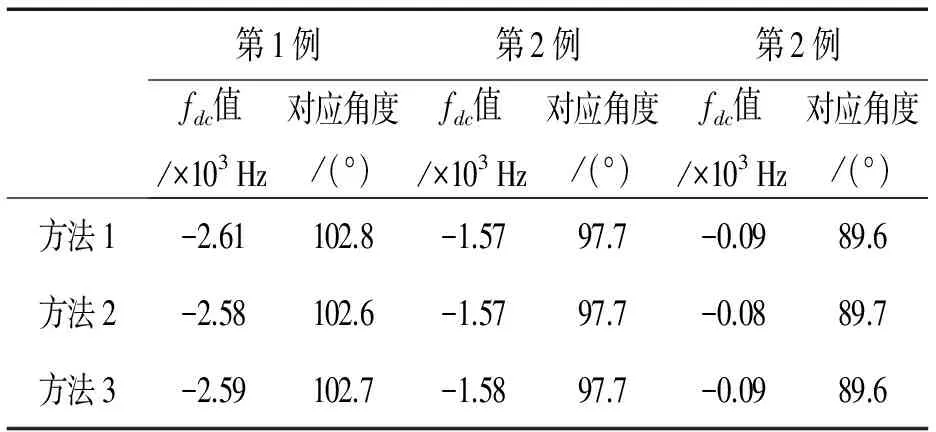
表3 非均匀场景下各种fdc估值方法结果比较

由处理结果可看出，改进的能量均衡法与传统的能量均衡法和时域相关法等方法相比，多普勒中心估值结果相差不大。但由于新方法避免了迭代运算，计算速度提高了。

6 结 论

多普勒质心估计一直是SAR信号处理中的关键步骤之一，传统的频谱能量均衡法是一种较为经典的多普勒质心估算方法，但当场景中存在强点目标时，利用该方法得出的估算值不够准确，而且由于该算法存在迭代运算，也不利于DSP实时处理。改进的能量均衡法较好地解决了这个问题，文章最后给出了MATLAB仿真和实测数据得到的结果，并给出了比较分析结论。

[1] LI F K. Doppler parameter estimation for spaceborne synthetic-apertrue radars[J]. IEEE Trans. GRS, 1985,23(1): 47-55.

[2] JIN M Y, et al.Optional Doppler centroid estimation for SAR data from a quasi-homogeneous source[J]. IEEE Trans. GRS,1986,24(6): 1022-1027.

[3] MADSEN S N, et al.Estimating the Doppler centroid of SAR data[J]. IEEE Trans. AES,1989,25(2): 134-140.

[4] JOHN C C, et al.Synthetic aperture radar system and signal processing[M]. John Wiley & Sons, INC., 1991.

[5] 孙泓波，顾红，等.机载雷达成像中的两种改进多普勒质心估计算法[J].兵工学报，2002，23(1)：49-53.

[6] 刘国庆，黄顺吉.星载SAR多普勒质心估计的改进方法[J].信号处理，1994，10(3)：156-160.

[7] 魏钟铨.合成孔径雷达卫星[M].北京：科学出版社, 2001．