解读符号学视角下的数学课堂交流

1 引言

近年来，符号学的观点被广泛应用在各门学科，如电影、戏剧、医学、建筑等，效果可观. 在数学教育中，研究者们将不同的符号学的理论和视角整合到已有的心理学、人类学、语言学和社会学的理论中，以便分析和更好地理解数学的教与学的过程. Sáenz-Ludlow等认为数学和数学的教学在本质上都是符号实践，其中，符号被发明、使用或再创造以使认知操作或目的变得容易.^[１]

数学对象的非物质的本性要求通过大量自然的表征（也就是，数学符号）来表达数学对象，以便它们能被社会地分享. 因此，学习数学既需要解释数学符号，也需要通过和他人交流来建构数学的意义. 这些解释和意义不是当场建构的，而是从个人在不同的数学、社会和自然的情景下大量紧密相连的经历中产生并不断发展的. 在这些经历中，多种符号系统（如语言、数学符号、手势）结合起来，为一个不断发展的数学意义的解释打下了基础. Sáenz-Ludlow基于Charles Sanders Peirce的符号学理论建立了一个名为“解释游戏”（interpreting game）的解释性模型，说明了数学课堂中思考和交流的相互依赖性，以及教师和学生参与的关于符号的解释.^[２]

2 从符号学视角分析数学课堂交流

数学交流需要自然语言、数学符号和其它符号系统中的手势及肢体语言. 因此，课堂交流展示了一种符号学的本性，这已经被数学家、数学教育者和心理学家直接或间接地承认. 任何个体的符号学活动呈现了社会互动的存在，但是关于社会互动在思维过程中的角色是首位还是第二位的辩论依然存在. 从符号学的视角看，个体的认知活动和社会互动都不是第一位的，它们以协作的方式共存，共同作用，以促进符号解释和产生意义的发展过程. 思考和交流（作为最广泛意义上的社会互动）是平行的，同时也是相互联系的. Peirce的符号学理论，提出了独特的原理来理解当符号被解释并转换成新的符号时，思考和交流之间的相互依赖性. 在Peirce看来，思考、符号、交流和产生意义有着内在的相互联系. 个体和集体使用符号和解释符号的过程，来源于社会互动，产生的结果是个人意义的构建. 这些个人意义将不断地被修正和改进，最终靠向圈内人已建立的常规意义.

Peirce是这样定义符号的，一方面它由对象决定，另一方面它又决定了人脑中的概念. Peirce称后者为符号的“解释项（interpretant）”，解释项由对象间接决定，因此存在符号、对象及解释项之间的三角关系. 符号给出了一个解释项来表示对象，有着认识论的功能，符号在它的对象和解释项之间是不可少的.^[3]

此外，Peirce认为符号不能称之为符号，除非它被解释或转化为另一个更充分发展的符号. 在这种转化中，符号被解释成新的符号，随之而来的是，更复杂的解释项和对象出现在了解释者的头脑中，从广义上来讲，解释项能被理解为一个符号向新的符号的转化（见图1）.

在符号向新的符号的不断转化中，伴随的一系列解释项逐渐形成了意义的产生. 这个转化的过程本身是解释的过程，通过这个过程，在符号施动者的头脑中符号逐渐被转化成较少情景化而更为一般化的符号. Peirce考虑了不同种类、不同功能的解释项. 这里我们考虑的是有意图的（intentional）、有效的（effectual）、交流的（communicational）和逻辑的（logical）解释项. 有意图的解释项是表达者头脑中的定义，有效的解释项是解释者头脑中的定义，有意图的解释项促使表达者（也就是意图者）为发送信息而选择符号，当意图者提出一个有意图的解释项，根据Peirce理论，解释者进行解释并产生一个有效的解释项. 最后，交流解释项是符号的意图者和解释者在交流中共同产生和分享的想法（即，达成的共识）. 其间有些解释项提出了推断和行为的计划，称之为逻辑解释项，它对带有他们自己的概念网的符号施动者来说是有意义的，在随后的交流计划中这些逻辑解释项进一步接受更改和修正.

Rotman曾指出，交流对数学家的创造性活动是必需的，因此交流对数学课堂中教师对学生的数学活动也应该是必需的.^[4]交流在本质上是一个连续的符号解释过程. 在这个过程中，教师和学生相互交换着他们作为意图者和解释者的角色，不断构建解释项并转化成新的符号（如，数学论据、图表、口头表达、手势或任何其它可视符号），以解释已确定的数学概念. 构建解释项意味着通过教师和学生主观的解释行为构造数学意义，这些解释行为决不是教师向学生过分简单化的信息转移.

师生之间的课堂交流要考虑到学生有意识并积极参与到解释过程，Sáenz-Ludlow把这种课堂参与者共同建构的解释过程称之为“解释游戏”（以下简称IG）. 一开始，数学符号对教师来讲可能是有意义的，但对学生来讲它们就是简单的毫无意义的书面记号. 通过IG，在学生的头脑中产生了解释项，给这些书面记号赋予了数学意义，即临时的个人意义，接受修正和改进. 随着IG的继续，临时意义越来越缺乏主观性，书面记号逐渐成为数学符号，产生了交流解释项，它们最终接近于数学概念的客观的标准的意义（见图2）.

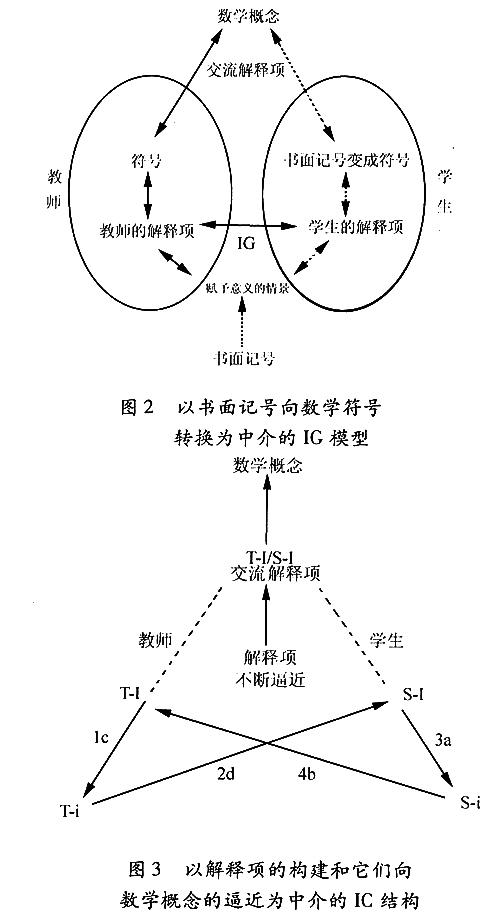
“解释循环”（interpreting cycle，以下简称IC）是IG的基本分析单元. 每一个IC都是以某一类型意义的建构为中介，为后续的循环做好准备，而在后来的循环中又会出现新的意义，接受修正和进一步的改进. 图3表示了解释循环的结构，数字1、2、3、4显示的箭向顺序表示了由教师发起的一个循环的开始方向；字母a、b、c、d显示的箭向顺序则表示由学生发起的一个循环的开始方向. 每个IC是通过解释、意图、解释项向新的符号的转化，以及某种达成共识的数学意义或交流解释项的最终出现组成的. 交流解释项不断进化，最终接近数学概念.

考虑一个由教师发起的循环，在教师对一个数学符号的解释行为中产生了一个有效的解释项（T-I），T-I引发了一个有意图的解释项（T-i）. 教师表达了她的有意图的解释项（T-i），学生进行解释以便产生一个有效的解释项（S-I）. 依次地，S-I引发了一个由学生表达的有意图的解释项（S-i），然后，教师解释学生的S-i进而产生了一个有效的解释项（T-I），T-I又引发一个由教师表达的T-i. 学生解释T-i，产生S-I，进而引发一个由学生表达的S-i. 由于有效解释项是存在于解释者头脑中的，我们只能通过表达出来的有意图的解释项来推断其有效解释项. 因此，当教师和学生在解释过程中建构和表达了有效的和有意图的解释项时（这可能产生逻辑解释项，也可能不产生逻辑解释项），IC一致继续直到某种交流解释项被表达出来.

课堂解释游戏是基于Peirce的符号学理论建立的解释模型，它把交流和社会活动的社会的与个人的维度，以及意义产生过程的公共的与私人的维度联系了起来，这样就突出了数学意义的合作构建过程. 解释游戏成为了教和学的工具，同时也应该变成提问的工具. 如何使学生参与解释，参与到解释游戏中，是数学教学面临的主要挑战之一. 为此，就有必要建立一种课堂环境，在这种环境下，师生之间的交流关系随着直接的和间接的智力结果自然地出现. 也就是，教师和学生应该被平等地置于交流关系的建立中，在这其中，符号使用、符号解释和提问变成了一个连续态.

3 结束语

新课标中强调，教学活动是师生共同参与、交往互动的过程，有效的数学教学活动是教师教和学生学的统一.^[5]那么教师如何才能组织有效的课堂交流呢？为了把解释游戏当作教与学的工具，教师应该认真考虑她的教学活动，这由两部分组成──备课和实际的教学活动. 备课活动应该是建立在和学生不对称的关系的基础之上，教师反省她自己对数学概念的理解，准备教学任务和教学策略以激发学生的好奇心. 在实际的教学活动中. 教师（很大程度上）应该维持与学生对称的对话，不要忘记她的指引作用，但要将学生的思维转换到她自己的思维范围之内. 因此，教师有必要学习区分她的解释项和她从学生的表述中推断出来的解释项，以便支撑和维持学生解释项到更精确的符号的连续转换.

成功的解释游戏可以推动符号使用、符号解释，以及书面记号转换成赋予较少主观性（即，更为客观）的数学意义的更成熟的符号. 在这些游戏中，教师和学生把他们自己作为有意识的解释的主体，教和学成为互补的活动，教师既教又学，学生既学又教，教师和学生在这个过程中都被授权教和学，形成一个活泼的互动.

参考文献

[1] Sáenz-Ludlow, A & Presmeg , N. Semiotic perspectives on learning mathematics and communicating mathematically[J]. Educational Studies in Mathematics, 2006, 61: 1-10.

[2] Sáenz-Ludlow, A. Classroom interpreting games with an illustration[J]. Educational Studies in Mathematics, 2006, 61: 183-218.

[3] 涂纪亮编, 皮尔斯文选[M]. 涂纪亮, 周兆平译. 北京：社会科学文献出版社, 2006. 219-302.

[4] Rotman, B. Towards a semiotics of mathematics[J]. Semiotica, 1988, 72: 1-35.

[5] 中华人民共和国教育部. 全日制义务教育数学课程标准[M]. 北京：人民教育出版社,2006.作者简介 庞雅丽，女，1980年9月出生，山西孝义人，华东师范大学数学系2006级博士研究生，研究方向为数学教育心理、中学数学教与学研究.