深海新型浮式生产钻井储油系统运动分析

陈矗立，范 菊，尤云祥

（上海交通大学 船舶海洋与建筑工程学院，上海200030）

1 新型FPDSO概述

近年来，由于中等和浅海的开发技术已经成熟以及当今世界大部分地区的浅海油气资源已日趋减少，因而深海和超深海油气开发已成为海洋开发的热点和必然趋势［1］。张力腿平台（TLP）可用于1 000m左右的水深，但其结构复杂，造价高，对水深过于敏感，庞大的重力和浮力以及作用于平台上的水动力载荷使其不适于更深海域［2］。而FPSO则是一种费用低廉的油田开采装置，集生产、储油、外输多项功能于一身，俨然是海上大型石油加工厂，顺应了海洋事业发展的要求，尤其适用于那些缺少大规模管道网络的地区。

美国Novellent LLC公司结合传统FPSO和TLP的优点，建设性地提出将带有钻井功能的隐藏式立管浮箱SRV（sheltered riser vessel）技术应用于FPSO，以适应西非2 500m深海域的特殊环境，并称这种新型海洋结构物为浮式生产钻井储油系统（FPDSO），见图1。

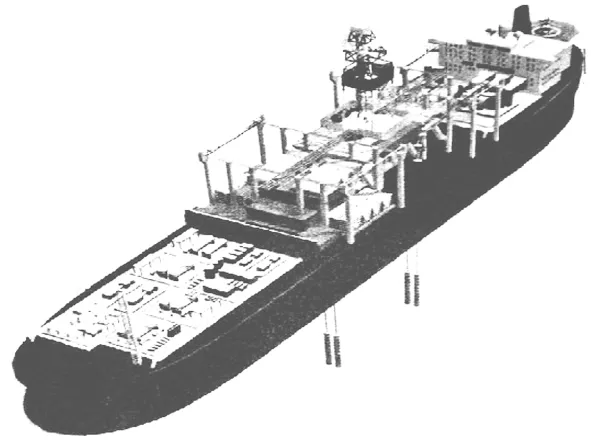
图1 浮式生产钻井储油系统

其中，SRV设计理念的功能类似于TLP，利用紧绷状态下的立管产生的拉力和上部浮箱的剩余浮力获取平衡［3］。其主要特点包括：

1）SRV位于FPDSO船体甲板中央的月井中，采用了月井外加防护板的保护措施，减少了一切环境载荷对它的作用，也基本不受FPDSO船体运动的影响，使得垂荡运动大大减少。

2）SRV能为立管系统提供足够的张力，完全满足极端深水情况下干式完井采用所必须的各种要求，克服了传统生产平台功能单一的缺陷，更有利于深海钻井采油作业的实施。

3）SRV与FPDSO船体相互独立，彼此通过活动装置连接，其立管的张力荷载不会对PFDSO船体的载荷产生影响，而FPDSO船体的纵摇和横摇运动，特别是垂荡运动也基本不会造成SRV立管张力的改变。

4）船形的传统FPSO外观设计，保持了FPDSO的经济型，灵活性和稳定性。

作为一种新型的海洋工程产品，FPDSO必须满足某一特定海况环境的要求。

2 FPDSO及SRV运动的理论分析

2.1 双物体耦合的势流理论

要正确评估FPDSO船体和SRV之间的耦合运动特征，必须仔细分析两个物体间的相互作用。简单起见，采用了一个双体系统，对每个单体采用势流理论计算［4-5］。坐标系统定义为平面位于静水面，见图2。

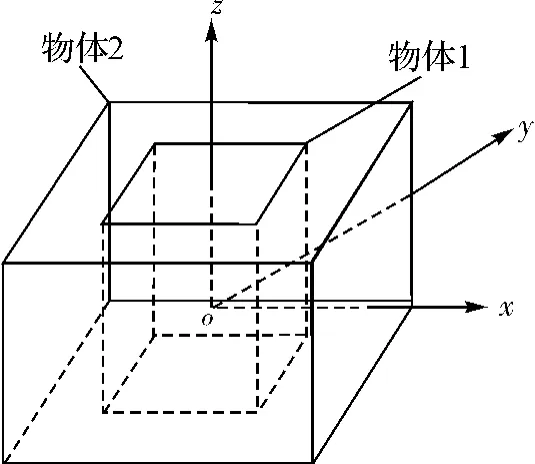
图2 双物体坐标系统

对于物体1（内部），在o1x1y1z1坐标系统的总速度势为：

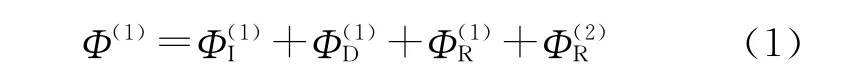
对于物体2（外部），在o2x2y2z2坐标系统的总速度势为：

式中：Φ（1）I、Φ（2）I——入射波速度势；

ΦD（1）、ΦI（2）——绕射势；

ΦR（1）、ΦI（2）——物体运动引起的辐射势。

假设作用于物体上的入射波为一阶近似，即为所熟知的余弦前进波。因而入射速度势可表示为：

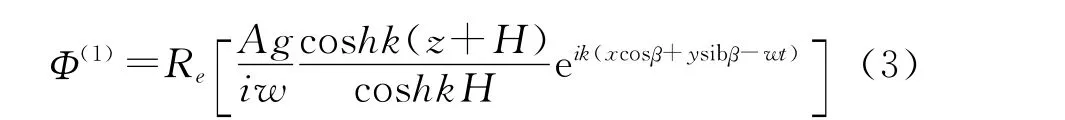
作用于物体上的外力，比如静水力和水动力可由贝努利方程求得。将（1）和（2）式代入贝努利方程，则作用于物体1和物体2上的水动力可表示为：

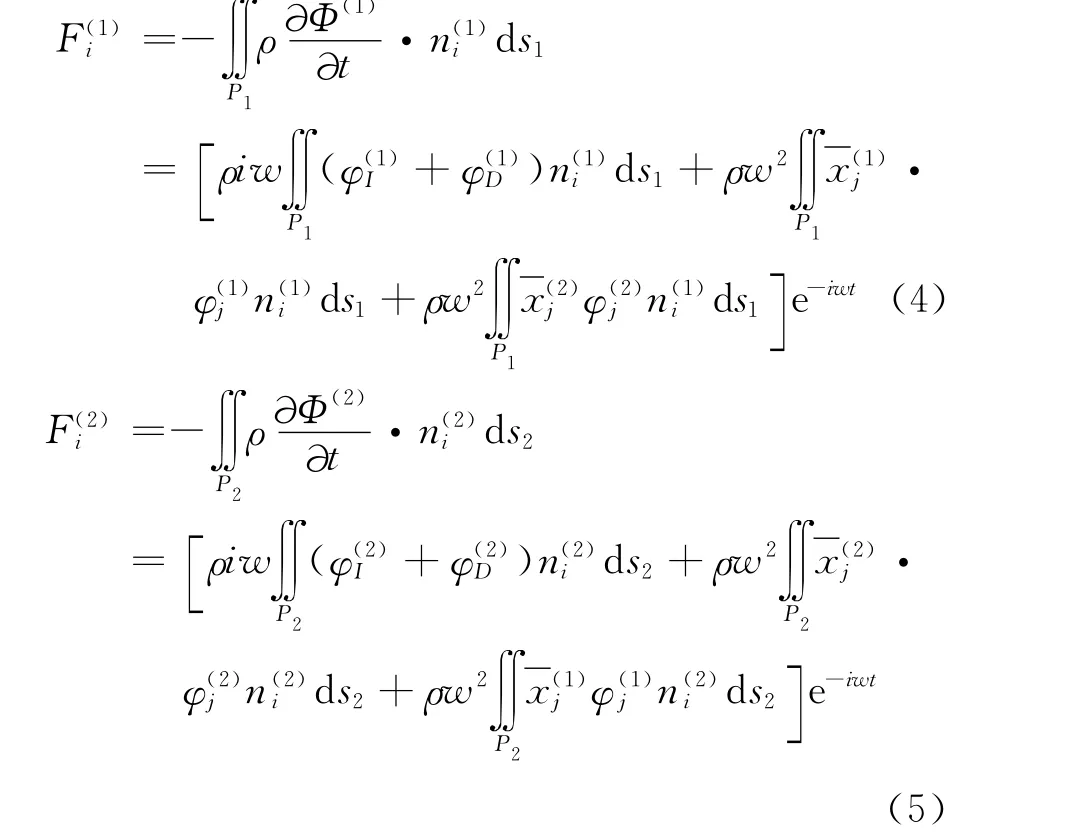
式中：n（1）i、n（2）i——指向物体内部的湿表面单位法向向量，（i＝1，2，3）。

（4）和（5）式中前两项分别表示作用于单个物体上的力，而第三项则表示两个物体间的相互作用力。

2.2 SRV的受力分析及运动

为方便起见，分析SRV在一个平面内运动时的受力，三维情况可依此类推。假设船体在迎浪或横浪情况下，其在波浪上的运动为（t）、1（t）（t），SRV 为（t）（t）（t），并且船体的运动不受SRV运动的影响。基于这种假设，由于防护垫和立管的约束而作用于SRV上的力和力矩如下。

1）x方向的力FSX为：

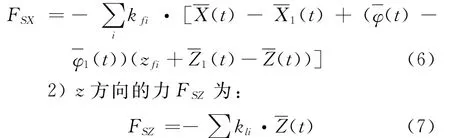
3）绕oy轴的力矩MSY为：

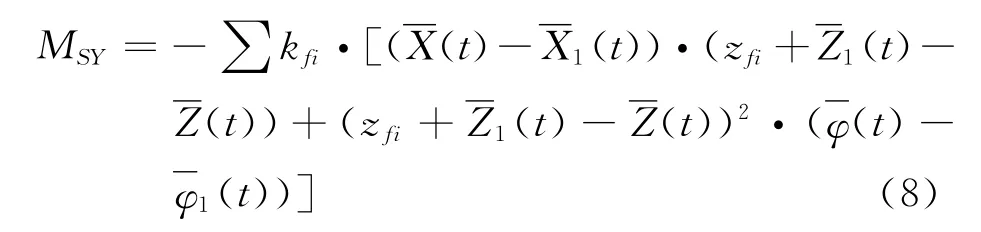
式中：ffi——第i个防护垫的刚度；

zfi——第i个防护垫的水平距离；

kli——i个立管的刚度。

文中只考虑一阶力的情况，因此假设附加质量和阻尼系数都是从线性理论中获得。由于两个物体之间的相互作用，作用在SRV上的水动力应该包括一个额外的部分，即由船体运动引起的。因此，SRV在月井中的垂荡运动公式可表示为：

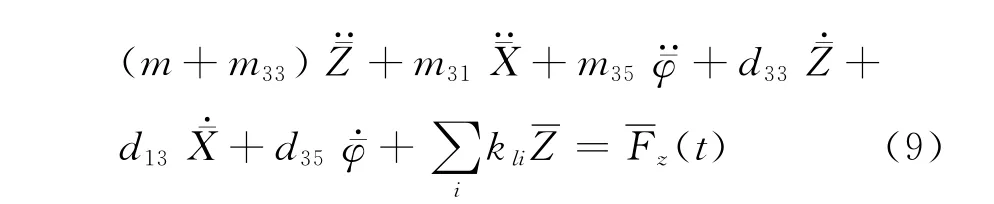
式中：mij——SRV的附加质量；

dij——阻尼系数；

i、j——相关的运动模态。

3 数值计算结果与试验结果的比较

模型试验在上海交通大学海洋工程国家重点实验室进行。由于不能对SRV的相关数据进行直接测量，试验通过对FPDSO船体和SRV之间的相对运动来间接的测量SRV的运动数据。实验中采用的环境条件为无风、无流，波浪谱采用JONSWAP谱，参数采用西非极限波浪的参数。缩比尺为1∶70，试验水深4.6m，锚系采用钢丝绳。表1和表2分别为SRV和FPDSO船体的主要技术参数。

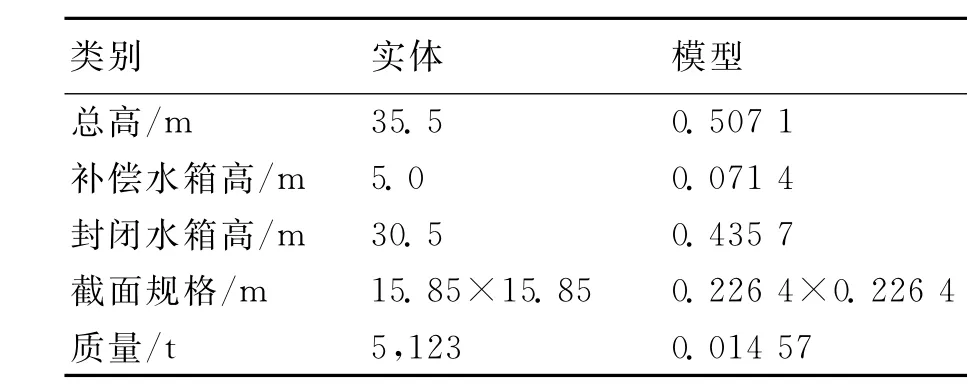
表1 SRV主要技术参数

表2 FPDSO船体主要技术参数

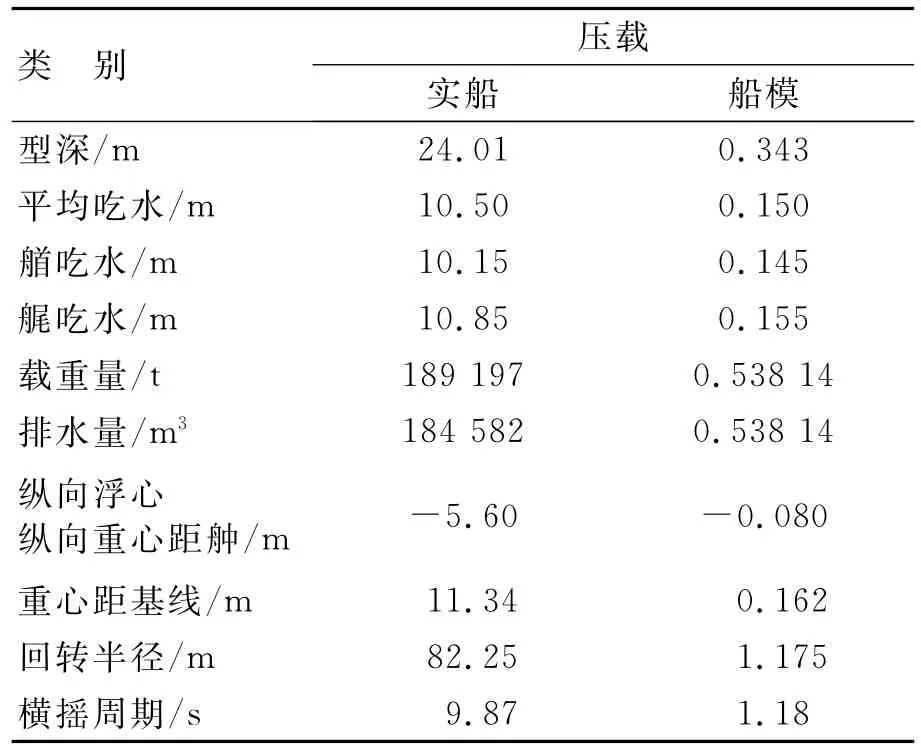
续表2

对于船形PFDSO，吃水较浅，横摇和纵摇运动的固有周期较短，固有频率在波频范围内，使得其以一阶运动为主，故对运动的分析只考虑与一阶力相关的垂荡、纵摇和横摇的相应结果。下面分别给出了相关运动的RAO（一阶运动的响应幅值算子）和统计值的比较。在本文涉及的模型试验中，载荷状态为压载，吃水为10.50m，浪向角为135°；原型及模型的有义波高分别为5.10和0.07m，对应的波谱周期分别为18.80和2.25s。

3.1 SRV的RAO及相关系数的比较

由图3可看出，对于相关系数在频率为0.7 rad／s之前，理论计算的垂荡RAO与试验结果吻合较好，且变化趋势大致相同。而在0.7rad／s之后，数值很低，试验结果可信度低，故试验与理论结果有些差别。

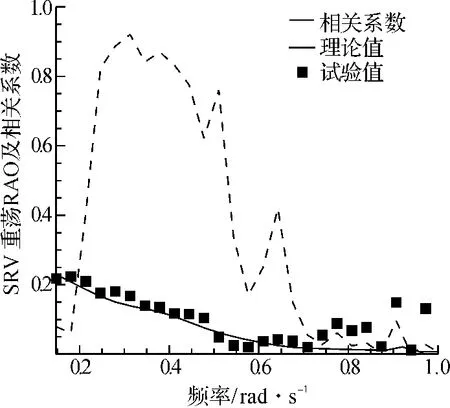
图3 SRV垂荡RAO和相关系数

3.2 PFDSO船体的RAO比较

由图4可看出，理论计算的垂荡、纵摇和横摇RAO与试验结果基本吻合，包括峰值位置以及峰值大小基本一致，且变化趋势大致相同。

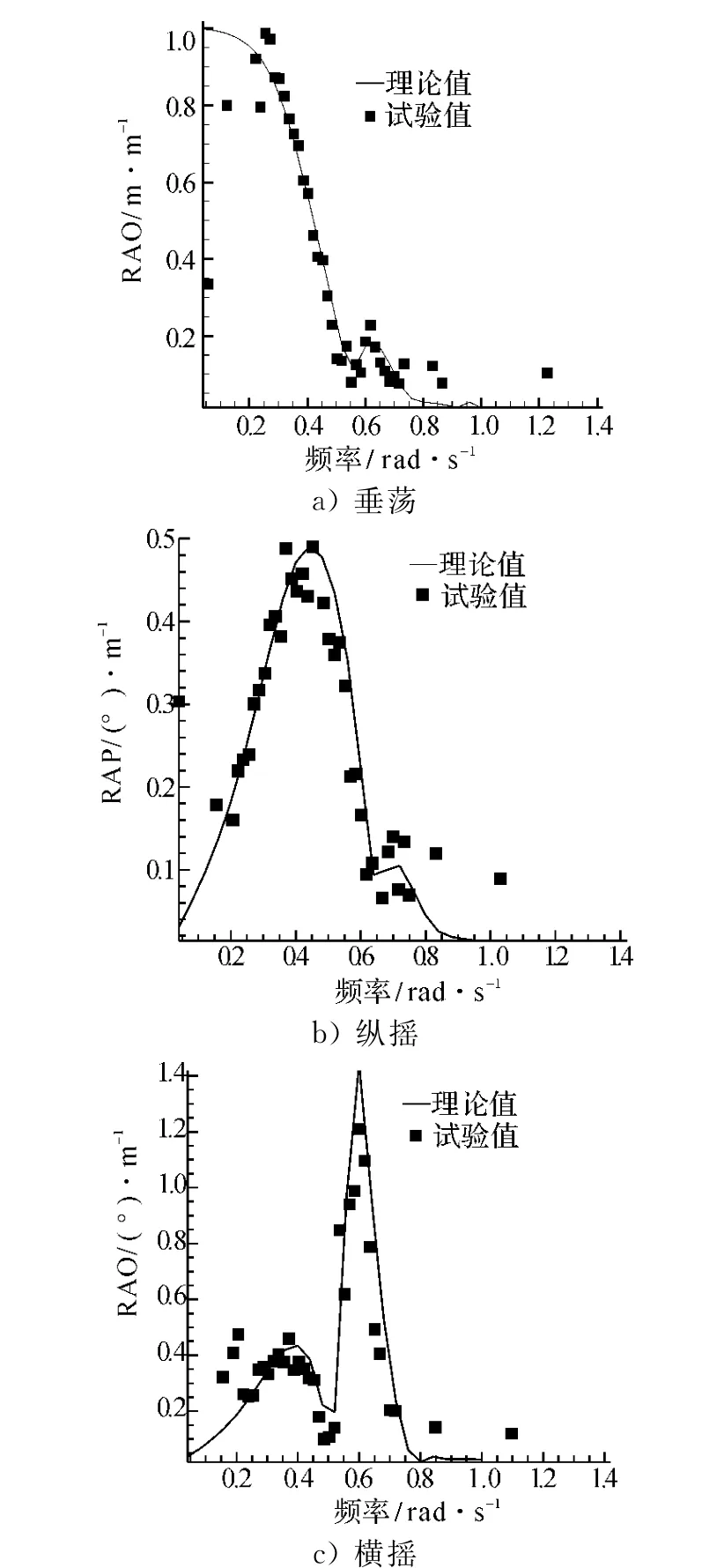
图4 RAO的比较

3.3 统计值的比较

表3所示为计算得到的FPDSO船体运动的垂荡、纵摇和横摇标准差以及SRV的垂荡标准差与相应的试验结果的比较。可见，垂荡、纵摇和横摇的标准差以及SRV的垂荡值与相应的试验结果基本接近。这说明本文采取的理论方法分析PFDSO在西非极限波情况下垂荡、纵摇和横摇运动特性的可行性。

表3 标准差的比较

综合比较图3、4中的垂荡RAO以及表3中的垂荡运动计算值和试验值，可以很明显地看到：无论是SRV的垂荡运动RAO还是统计值的结果都大大的小于PFDSO船体相对应的结果。这说明，SRV设计理念的采用，的确大大减少了其受到的环境载荷的影响，使得深海钻井和采油作业可以在同一个平台进行，大大减少了平台的作业周期并降低了相应的成本。

4 分析结果与讨论

从以上的分析比较中可以看出，理论分析的结果和试验结果无论从运动RAO，还是统计值上都基本吻合。对于系泊深海平台，由于锚系处于张紧状态，对FPDSO船体的水平运动以及锚系张力的分析，需要进一步发展浮体与锚泊系统相耦合的时域程序，以完善理论。

在西非极限波情况下，垂荡运动的标准差在0.86m以内，横摇运动在0.55°之内，纵摇运动在0.50°以内，除垂荡外，平台总体运动较小。在真实的西非海况下，需将风、流等的情况加入。

PFDSO由于采用了FPSO和TLP设计的优点，既保持了FPSO的经济性和灵活性，又保持了TLP适应深海采油的良好动力特性，SRV设计理念的采用，大大降低了其垂荡运动。在西非极限波情况下，SRV垂荡运动标准差在0.2m以内。这使得这种新型浮式生产钻井采油系统在将来的深海石油开采中具有一定的优势。

［1］金 秋，张国忠.世界海洋油气开发现状及前景展望［J］.国际石油经济，2005（3）：43-44.

［2］李 波.新型采油平台——浮式塔的一阶动力响应及二阶定常慢漂力［D］.上海：上海交通大学，1999.

［3］John Allen Mercier Ltd.，et a1.Evaluation of button TLP response to environmental loads［C］.OTC4429，Houston，1982.

［4］S.Chen and O.Mahrenholtz.Dynamic Responses of Floating Twin Bodies in Beam Waves［C］.International Offshore and Polar Engineering Conference，1992.

［5］刘应中，缪国平.船舶在波浪上的运动理论［M］.上海：上海交通大学出版社，1986.