改进D-S算法在船舶汽轮机故障诊断中的应用研究

1.中国舰船研究设计中心 武汉 430064；2.海军驻426厂军代表室 大连 116000

船用汽轮机结构和系统的复杂性、运行环境的约束等因素导致汽轮机的故障率较高，而且故障的危害性很大，所以汽轮机的故障诊断技术一直受到高度关注[1]。在故障诊断过程中，由于检测量与故障特征之间、故障特征与故障源之间往往呈现为典型的非线性关系，很难用现有的函数关系来描述，故在近几年，逐渐有研究人员将证据理论运用到汽轮机的故障诊断中来，在一定程度上提高了诊断的正确性。

但是在应用过程中，会出现由于故障诊断系统中某一传感器的失效而导致整个诊断系统出现颠覆性的判断错误，针对这种情况，将D-S证据理论进行了改进，选用人工神经网络对各种数据进行了前期局部诊断，从而提出了一种基于改进证据理论的船舶汽轮机综合诊断算法。

1 数据融合及证据理论

数据融合是一种多源信息综合处理技术[2]，利用了计算机技术对按空间顺序获得的若干传感器的信息在一定准则下加以分析、处理和综合，得到比单一传感器更全面、正确的决策。

根据数据融合所处理的信息层次，可将数据融合由浅到深分为数据层融合、特征层融合、决策层融合，其实质是根据一定的准则和每个决策的可信度由计算机模拟专家思维做出最终判断。

D-S证据理论的基本概念是在有穷而互相排斥的陈述组成的完备集Θ中任何命题A都应包含在2Θ中，定义映射m：2Θ→[0，1]且满足：

m(Φ)=0，

称其为基本概率分配函数BPAF。对假设命题A的支持度和可能性，分别定义为信任函数Bel(A)和Pl(A)。D-S证据理论提供的合成公式能合成多个证据源的证据。

2 证据理论在应用中的失效问题

由于振动是汽轮机状态最常见的外部表现形式[3]，当机组的状态发生变化时，其振动状态会随之发生改变。所以，通过检测汽轮机在运行中产生的振动信号进行故障诊断是目前最常见的诊断手段。在进行故障诊断时，可用多个传感器来对不同位置进行测量，得到的振动信号经FFT变换后提取一定数量的特征后作为BP神经网络的输入，随后进行D-S证据理论，可假设状态识别框架为Θ={f0，f1，f2，f3}，其中f0为正常状态，f1为摩擦故障，f2为不对中故障，f3为不平衡故障。故障诊断过程就是对辨识框架中的每个命题进行正确的鉴别。

尽管D-S证据推理理论比传统的概率论能更好地把握问题的未知性和不确定性，通过证据的累积逐步缩小假设集，大大地提高识别准确率。但由于不同传感器安装位置的不同，导致它们对不同类型的故障和不同位置的故障的敏感度不同，因而每个传感器神经网络输出结论的可靠性和精度也不相同，同时，如果某个传感器出现故障，这时就可能造成D-S合成算法失效。

设Θ={f0，f1，f2，f3}，有几个基本概率分配为：

m1(f0，f1，f2，f3)=(0.9，0.1，0，0)，

m2(f0，f1，f2，f3)=(0，0.1，0.9，0)，

m3(f0，f1，f2，f3)=(0.9，0.05，0.05，0)，

…，

m6(f0，f1，f2，f3)=(0.95，0.01，0.02，0.02)。

应用D-S合成计算出

=1-(0.9×0.1×+0.9×0.9+0.1×0.9)

=0.01

即k=100 、m1、m2合成后的结果为：

m(f0，f1，f2，f3)=(0，1，0，0)。尽管m1、m2对f1支持度都非常低，但结果却认为f1为真。这表明若诊断系统中有某个证据因为传感器故障而导致测量错误，会引起整个系统诊断决策的错误。虽然Ronald R.Yager将D-S进行了改进[4，5]，但对于证据源个数多于2时，合成结果并不理想，而汽轮机组的数据源大多数大于2个，因此，有必要将D-S合成公式进行改进，避免这种小概率时间出现而影响整个诊断系统。

3 对证据理论的改进分析

通过以前的D-S合成算法知道，在两冲突证据合成后的新证据结论可以排除干扰，确定最终结论，而不是将冲突全部划归为不确定因素，尽管证据之间冲突越高可利用的东西越少，但至少是很少部分可用的，剩下不可用部分划归到不确定区间，这与Ronald R.Yager的改进合成公式不同。同时，可得到冲突可用率是冲突的减函数，可定义一个冲突可用率函数来量度这种关系。冲突为0时，即无冲突时，可用率最高，其值为1；冲突为1时，完全不可利用，可用率最低，其值为0；冲突在一般较小值范围变化时，可用率其变化所对应D-S合成算法中的k变化较小，冲突在较大值接近1附近变化时，可用率其变化所对应D-S合成算法中的k变化很大。

在此，定义新的合成公式为：

m(Ø)=0

m(A)=mp(A)+λμ·mq(A)A≠Ø，Θ

(1)

m(Θ)=mp(Θ)+λμ·mq(Ø)+λ(1-μ)

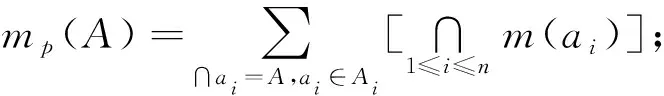
由

可知

λ=(1-k-1)

设m1，m2，…，mn对应的证据集为：A1，A2，…，An；假设证据集i，j之间的冲突大小为λij，则有：

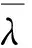
(1)式可以写成

m(A)=k·mp(A)·(1-λ)+λ·μ·mq(A)

第一项中的k·mp(A)就是D-S合成公式。当λ值较小时，这时证据冲突较小，上式的第一项起主要作用，合成效果近似于D-S合成。当λ值较大时，即说证据冲突较大，合成结果主要由μ·mq(A)项的大小决定。μ为整个证据冲突的可用率函数，μ·mq(A)为证据对A元素分配的可用率，也可以看作冲突λ调节的是非空集元素概率赋值和空集Ø的比例关系，而可用率函数μ调节的是元素A合成基本概率赋值和不确定基本概率赋值Θ之间的比例关系。

4 改进后合成公式的应用

根据以上改进思路，在此，取一组数据比较改进算法的效果，该组数据为高度冲突证据数据。

设Θ={a1，a2，a3}，多个基本概率分配为：

m1(f0，f1，f2，f3)= (0.9，0. 05，0.05，0)，

m2(f0，f1，f2，f3)=(0，0.1，0.9，0)，

m3(f0，f1，f2，f3)= (0.9，0. 05，0.05，0)，

…，

m6(f0，f1，f2，f3)= (0.9，0. 05，0.05，0)。

高度冲突证据情况下证据合成的D-S证据推理合成方法和新改进的合成方法效果比较见表1。

表1 高度冲突证据合

比较不难发现，对于第一组高度冲突的证据f0和f2，由于传感器故障而导致在使用D-S公式进行诊断时出现错误，而本文提出的改进公式的一次合成结果f0不为0，是因为此时的证据冲突可用率μ很低，合成后对它们的支持也很低，但不确定度较大，反映了对该冲突由于不知道引起的不确定；随着支持f0的证据的不断加入，这种不确定因素在减小，冲突可用率μ较高，合成后对f0的支持也不断增大，与人们的思维相符，也说明了改进的合成公式的合理性。

5 结论

汽轮机组是一个较为复杂的系统，其故障诊断系统监测点较多，因此反映系统状态的参数也很多，导致了诊断系统的不确定性也增大。将传统的D-S融合算法进行改进，避免了合成过程中某一证据因传感器故障而造成高度证据冲突导致整个系统的决策失误，从而影响诊断系统运行。通过对比分析改进后的算法公式与原来的算法公式在实际故障诊断系统中的应用，得出改进后的算法公式使得诊断系统的可信度可明显提高，有一定的实际应用价值。

[1] 吴今培.智能故障诊断与专家系统[M].北京:科学出版社，1997:8-15.

[2] 杨万海.多传感器数据融合技术及其应用[M].西安:西安电子科技大学出版社，2004:2-4.

[3] 船用汽轮机与燃气轮机[M].北京:人民交通出版社，1996:88-90.

[4] 邓 勇,施文康.一种改进的证据推理组合规则[J].上海交通大学学报, 2003(8):1275-1278.

[5] Ronald R.Yager. On the dempster-shafer framework and new combination rules[J]. Information sciences, 1987,41:93-137.