非线性PID控制器在潜艇深度控制中的应用

，

(1.海军潜艇学院研究生队，山东 青岛 266071；2.海军潜艇学院作战指挥系，山东 青岛 266071)

潜艇运动系统是一个大惯性、非线性、环境干扰复杂的系统，难以用一个精确的数学模型来描述。如今普遍采用国际标准的潜艇六自由度方程与真实的潜艇运动也有一定的差异。

非线性自抗扰PID控制器[1-2]弥补了传统PID控制方法的不足。

仿真采用的潜艇在垂直面内运动的非线性方程见文献[3]。

1 PID控制器自抗扰控制算法

自抗扰控制器的核心原理是把系统的未建模动态和未知的外扰作用都归结为对系统的“总扰动”进行估计并给与补偿。

利用微分跟踪器和状态扩张观测器设计的潜艇深度控制器见图1。

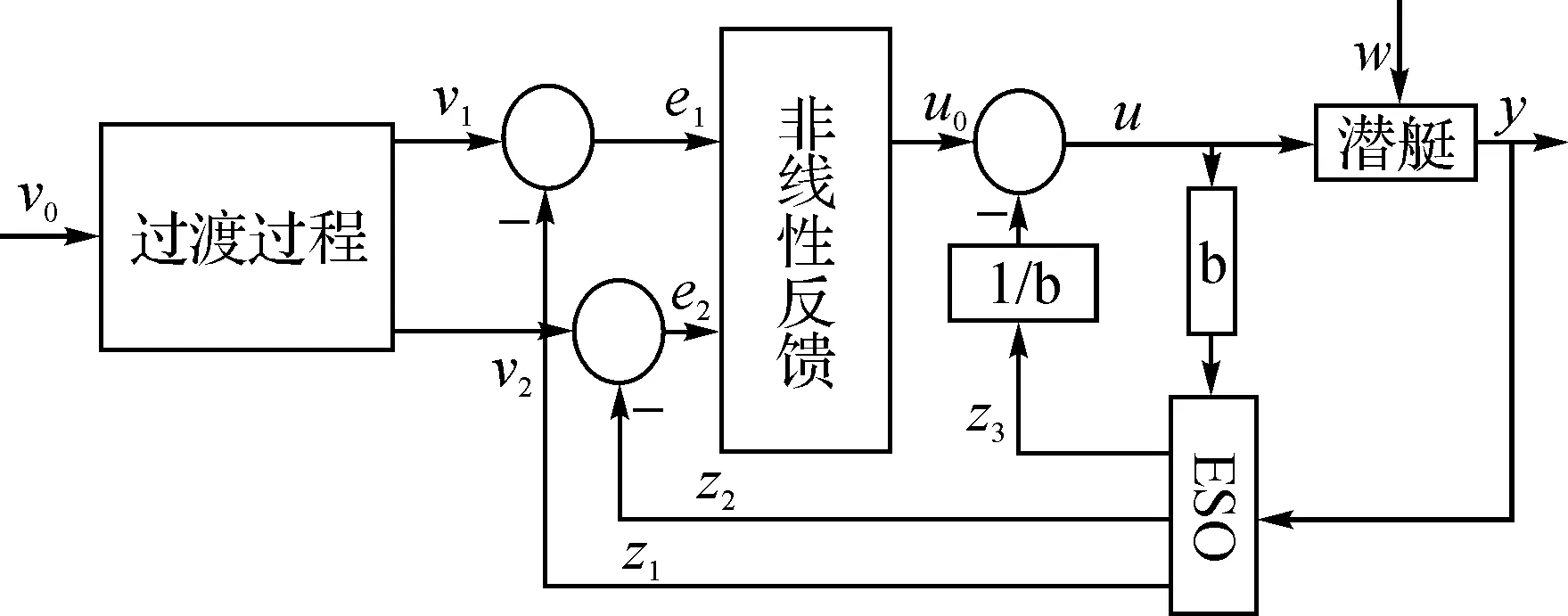
图1 非线性PID控制器方框

以深度控制为例，进行自抗扰控制器的设计。纵倾角控制类似。ξ0、θ0为设定的潜艇深度和纵倾角度。

1) 过渡过程。

v1(k+1)=v1(k)+hv2(k)

v2(k+1)=v2(k)+hfst(v1(k)-

ξ0,v2(k),r,h1)

(7)

式中：fst(v1(k)-ξ0,v2(k),r,h1)参见文献[2]。

2) 状态扩张观测器。

ε1=z(k)-y(k)

z1(k+1)=z1(k)+h(z2(k)-β01ε)

z2(k+1)=z2(k)+h(z3(k)-

β02fal(ε,α1,δ)+bu(k))

z3(k+1)=z3(k)-hβ03fal(ε,α2,δ)

(8)

3) 控制量的形成。

e1=v1(k)-z1(k)

e2=v2(k)-z2(k)

u0=β01fal(e1,α1,δ)+β02fal(e1,α2,δ)

u(k)=u0-z3(k)/b

(9)

(10)

深度变换的快慢取决于所用航速和指令纵倾角。实际操纵控制中，利用模糊查询深度与纵倾角的对应关系，较大深度差变换时利用首、尾舵控制纵倾，一定深度范围内通常利用首舵控制深度。利用尾舵控制纵倾，这里也采用这种方法，具体的控制工程由自抗扰PID控制器完成。

2 仿真分析

利用matlab/simulink仿真工具分别对不同深度的控制进行仿真。航速6 kn，深度初始下潜为100 m,指令纵倾角为-9°，利用叠加的正弦干扰力模拟波浪作用力，以及通过加入常值干扰和瞬时的突变力，来分析控制器的鲁棒性。

结果见图2～5。为了对比明显，通过实艇试验调节获得。

可以看出，非线性自抗扰PID控制器较好的实现了快速性和超调之间的矛盾，并且在相同的纵情指令下，非线性自抗扰PID控制器比常规的控制器使得潜艇能提前且无静差地到达指令深度；对比图3、图5可以看出在抑制干扰方面非线性自抗扰PID控制器也表现了比较好的效果。

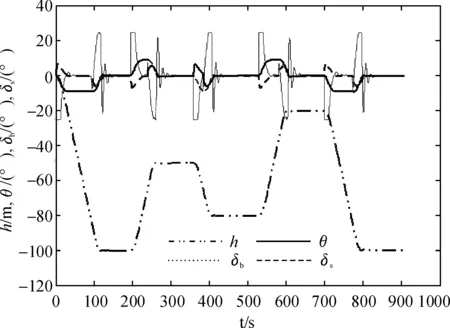
图2 无干扰情况下非线性自抗扰PID控制器深度控制仿真

图3 有干扰情况下非线性自抗扰PID控制器深度控制仿真

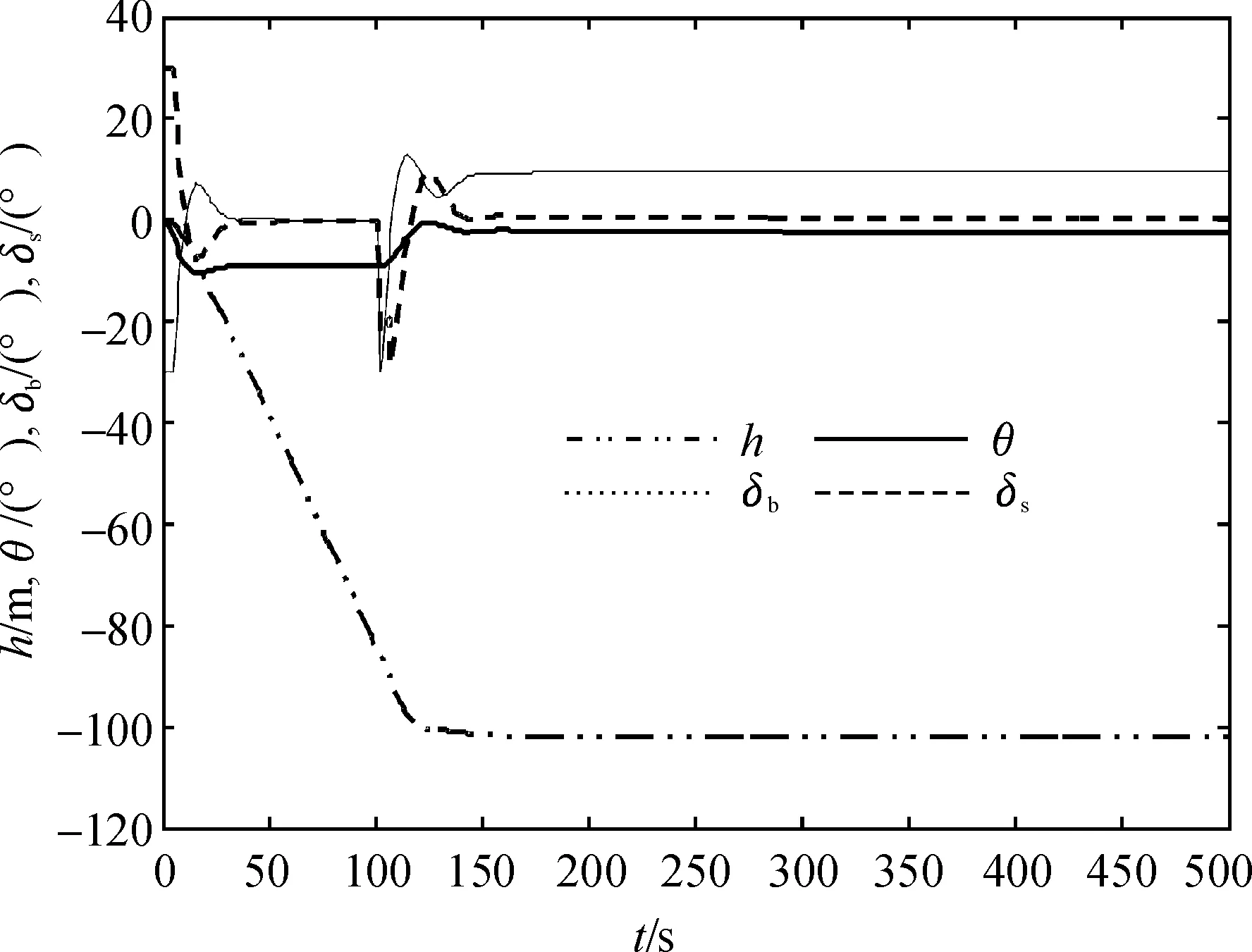
图4 无干扰情况下常规PID控制器深度控制仿真

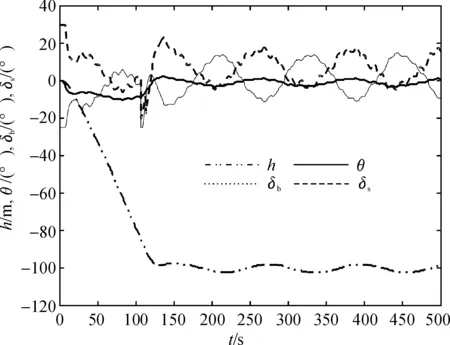
图5 有干扰情况下常规PID控制器深度控制仿

在实际仿真时，非线性PID控制器的参数调节比常规的PID较易，且不同的深度差异变换非线性PID控制器可以实现无超调；而常规的PID控制器的控制效果对控制参数比较敏感，具体调节中比较繁琐。

3 结论

针对潜艇垂直面运动模型，这种二阶、多变量耦合，非线性较强的系统，通过上述仿真分析，不能看出，通过适当的安排过渡过程，避免了深度变换过程中的超调现象，同时又解决了快速性的问题。

另外，在控制器的设计上，控制器的微分量，不是直接通过误差来提取的，而通过跟踪微分器来获取，对不连续的参考输入可以合理的提取微分信号；另外，自抗扰非线性PID控制器避免参数多带来的不便，使得参数调整远比常规的PID控制器参数的调节容易的多。实用上有较好的前景。

[1] 韩京清.自抗扰控制器及其应用[J].控制与决策，1998(1)：20-23.

[2] 韩京清.从PID技术到“自抗扰控制” 技术[J].控制工程，2002(5)：13-18.

[3] 徐亦凡，潜艇操纵原理与方法[M].北京：兵器工业出版社，2002.