波浪补偿平台垂向位移的短时预报

，，，

(华南理工大学 交通学院，广州 510640)

为了减少船舶在风浪中的摇摆和升沉运动对某些海上作业和设备的影响，需在其上构建一个具有波浪运动补偿功能的稳定平台系统。该系统中采用预报控制的策略，即先对波浪运动补偿稳定平台控制点的垂向位移进行短时预报，然后将预报值转化为控制信号输入到补偿执行机构，对平台的波浪运动进行补偿。

时间序列分析与预报理论中，线性自回归(AR)模型和线性自回归滑动平均(ARMA)模型应用在非线性系统预测中取得的效果不是很理想。动态回归神经网络提供了一种极具潜力的选择，它能够更生动、更直接地反映系统的动态特性,代表了神经网络建模、辨识与控制的发展方向[1-2]。Elman网络是一种典型的动态神经元网络，它是在前馈网络基本结构的基础上，通过存储内部状态使其具备映射动态特征的功能，从而使系统具有适应时变特性的能力。波浪补偿平台垂向位移预测模型一般为非线性函数，并且具有动态特性，因此采用Elman神经网络对波浪补偿平台垂直位移预报进行建模和分析。

1 Elman网络预报模型的建立

1.1 Elman神经网络结构

Elman网络由四层组成，分别为输入层、隐层、承接层和输出层，见图1。承接层神经元的数目与隐层神经元数目相同。网络的主要特点是隐层输出通过承接层单元延迟、存储、自联到隐层输入，从而使网络对历史状态数据具有敏感性。同时，由于网络内部增加了反馈连接，使网络具有处理动态信息的能力，有利于动态过程建模。

图1 Elman神经网络的结

1.2 Elman网络的数学模型

结合图1，Elman神经网络的数学模型可描述为：

Hj(t)=g(Vj(t))

式中：p、q、r——输入层、隐层和输出层神经元的个数，承接层神经元的数目与隐层神经元数目相同；

Ii(t)——Elman网络的第i个输入；

Vj(t)——第j个隐层神经元的输入和；

Hj(t)——第j个隐层神经元的输出；

Ok(t)——输出层第k个神经元的输出；

wkj——隐层与输出层神经元的连接权；

wja——承接层到隐层神经元反馈连接权；

wji——输入层与隐层神经元之间的连接权；

Hja(t-1)——隐层神经元的一步延迟输出；

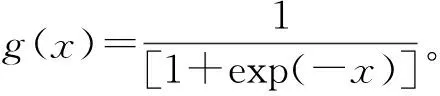
1.3 改进BP学习算法

经典反向传播算法在实际应用中存在两个主要问题：收敛速度慢和目标函数存在局部极小点。因此采用学习训练算法即自适应学习速率动量梯度下降反向传播算法对反向传播算法进行改进[3]，来克服上述缺点。该算法结合了动量梯度下降算法和自适应学习速率梯度下降算法，可以提高Elman网络的训练速度和稳定性，并且可以有效地避免出现局部极小点。

1.3.1 动量梯度下降法

动量梯度下降法可以降低网络对误差曲面局部细节的敏感性，有效地抑制出现局部极小的问题。此外，对权值更新时，由于考虑相继时刻的梯度方向，提高了学习稳定性和收敛速度。其网络学习算法为:

η——学习率,η>0;

α——动量因子,0≤α≤1。

所加入的动量项实质上相当于阻尼项，减小了学习过程的振荡趋势，改善了收敛性。

1.3.2 自适应学习率梯度下降法

学习率对整个训练过程有很大的影响。学习率选得太小,则收敛太慢；而如果学习率选得太大，则有可能修正过头，导致振荡甚至发散。如果在训练过程中合理地改变学习率，就会避免以上缺陷。

自适应调整学习率的改进算法有利于缩短学习时间,其学习算法为:

η(t)=2λη(t-1)

如果连续两次迭代梯度方向相同，表明下降太慢,这时学习率加倍;如果连续两次迭代梯度方向相反,表明下降过头,这时学习率减半。

从上述分析归纳出，自适应学习速率动量梯度下降学习算法为：

2 试验数据采集、处理及预报

2.1 试验数据采集和处理

模型试验在华南理工大学交通学院港口与航道实验室中进行，港池长32 m，宽18 m，高1 m，蓄水深度为0.8 m。港池一端装有造波机，另一端铺有1∶7的消浪斜坡，可消除90%的反射波。试验采用规则波进行模拟，取波浪周期为1.4 s，波高0.06 m，数据采集间隔时间为50 ms。试验中稳定平台模型的运动(横摇，纵摇和垂荡)是通过测量布置在模型的不同位置的4个传感器的垂直位移，经A/D变换及计算机采集，进一步转换计算得到。

数据的预处理主要是指对时间序列数据进行相应处理得到合乎平稳性，正态性，零均值要求的时序性数据。同时，数据预处理还包括野点的剔除和数据平滑问题[4]。

剔除野点。由于实验环境、测量设备以及传输设备精度的影响，所采集的数据可靠性难以得到保证，存在遗漏数据和数据错误的可能性，应想办法除去这些数据野点。通过粗略建立AR模型，求出残差，残差太大的数据点为野点。然后用AR算法得到的值代替野点处的值，重新建模直至数据平滑。另外还可通过加入信号低通的方法除去数据突变的点。

为了有效地利用Sigmiod函数的特性，以保证网络神经元的非线性作用，实验数据在输入Elman网络之前需要进行归一化处理，相应地,也需要对训练后的数据输出进行反归一化处理。

2.2 学习训练及预报

数据经处理后，利用Matlab中的神经网络工具箱建立Elman网络模型，并编制相应的语言程序。隐含层神经元采用tansig函数作为传递函数，输出层神经元传递函数为纯线性函数purelin。网络学习算法为改进的BP算法即自适应学习速率动量梯度下降反向传播算法其对应的训练函数为traingdx函数。Elman网络作为波浪补偿平台控制点垂直运动时间序列模型，输入和输出神经元分别为5个和1个。经过试算，当选择隐层神经元为15个时,所建立的网络模型具有较好的预报精度和较快的收敛速度。

网络训练主要参数设置如下：训练次数为10 000;学习速率为0.01；学习速率增长和下降比例因子分别为1.05和0.70；动量常数为0.9；网络性能目标为0.006；网络性能函数的最小梯度为1×10-10;当训练次数或性能目标或性能函数的最小梯度达到设置要求时，网络训练停止[5]。

3 计算结果及分析

1) 图2和图3给出了Elman网络模型训练误差曲线。从图中可以看出采用BP算法的Elman网络在训练到6 554次时，达到网络性能目标0.006。而改进反向传播算法的Elman网络训练只需训练187即可达到性能目标，具有更快的收敛速度。

图2 采用反向传播算法网络训练误差曲

图3 采用改进反向传播算法网络训练误差曲

2) 以自适应学习率动量梯度下降反向传播算法进行学习训练的前馈网络预测模型和Elman网络预测模型对波浪补偿平台控制点垂向位移的预报结果见图4、5。

图4 前馈网络的预测结果

图5 Elamn网络的预测结果

从图中可以看出以Elman网络和前馈网络作为波浪补偿平台控制点未来0.2 s(波浪补偿平台控制点垂直位移短时预报要求)垂向位移预报模型都具有较好的效果。但是相对前馈型网络预报模型而言，Elman网络预报模型的位移预报曲线和实际位移曲线更加贴近，即预报误差比前馈网络预报模型的预报误差更小。因此，采用Elman网络模型进行预报具有一定的可行性。

[1] Elman.J L.Finding structure in time[J].Cognitive Science, 1990, 14: 179-211.

[2] Masumi.Prediction of time series by a structure learning of neural network [J].Fuzzy Sets and System, 1996, 82:167-176.

[3] 韩万林,张幼蒂.用改进算法估算矿石品位[J].系统工程,2000,9(3):80-82.

[4] 沈 艳.神经网络理论研究及在舰船运动预报中的应用[D].哈尔滨：哈尔滨工程大学,2005.

[5] 董长虹.Matlab神经网络与应用[M].北京：国防工业出版社,2005.