舰船燃气轮机燃气初温的热经济学优化分析

，

(海军工程大学 船舶与动力学院,武汉 430033)

热力学第一定律定律、第二定律以及熵分析等热力学分析法是单纯从理论角度提高能量利用率的热力学分析方法，但在工程实际应用中，所得结论往往由于经济、生产工艺、材料设备、环保等因素的制约而难以实现，因此单纯的热力学分析方法不能解决节能与经济、环保等因素之间的矛盾。热经济学是一门融热技术与经济为一体的综合学科，对能量系统的热经济最优化运行研究是其一个重要应用。

舰船燃气轮机应用于巡航工况时有三个要求，一是保证舰艇一定的动力即舰船的航速，二是减少对动力装置的损耗以延长其寿命，三是减少能源消耗以保证舰船一定的续航率和经济性。舰船对动力装置的使用要求就以上三点而言是相互制约的。综合考虑各个因素的影响，以燃气轮机全寿命周期中单位小时费用为目标函数，以燃气初温作为决策参数进行热经济学优化分析，从而得出了优化参数。

1 目标函数的建立

运用热经济学分析方法对热力系统的热力学参数进行优化的关键是确立优化参数与目标函数之间的函数关系。对本文而言，关键是找出燃气初温与装置的经济效率以及与装置的折旧率之间的关系。

1.1 热力学模型

在理想简单循环中,工质在燃气轮机中依次实现等熵压缩过程、等压燃烧过程、等熵膨胀过程和等压放热过程。如图1 所示，1→2线表示在压气机中的等熵压缩过程,2→3线表示在燃烧室中的等压燃烧过程,3→4线表示在高压涡轮中的等熵膨胀过程, 4→1线表示等压放热过程。

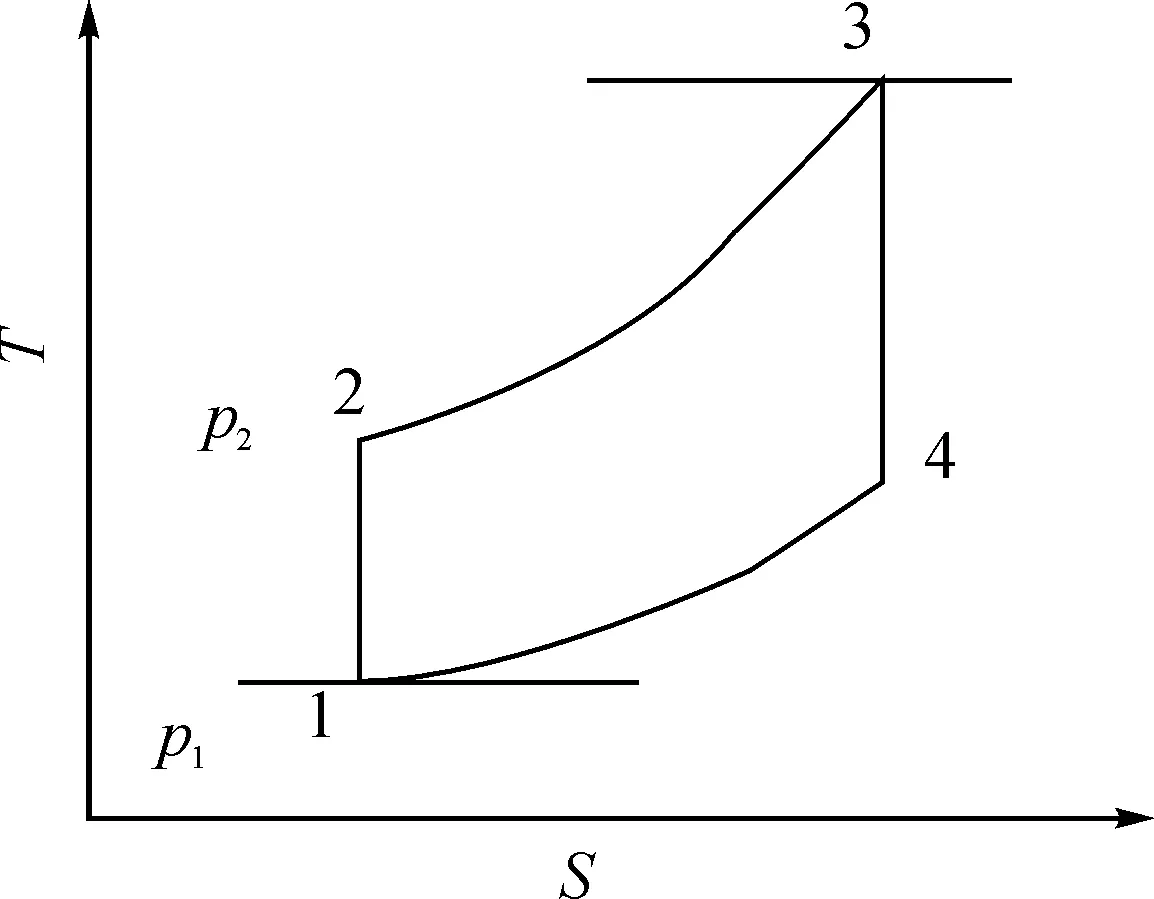
图1 燃气轮机理想热力学循

由热力学第一定律和第二定律可得到循环功的计算方程[1]，理想循环比功最大值为：

(1)

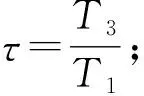
T1——大气温度；

T3——燃气初温；

Cp——定压比热容；

对应的温比与最佳压比之间的关系为：

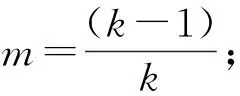
k——比热容比。

装置的热效率

(2)

由能量守恒定律可得

Hμbηmax=3 600Ne

(3)

式中：b——耗油率；

Hμ——燃料低热值；

Ne——机组额定功率。

方程式左边为每小时燃烧的燃油所发出的全部有效热量，右边为发动机每小时所做的功。

由式(1)、(2)、(3)可得到耗油率与温度的关系式

(4)

由式(4)可知，如需发出相同的功率，工质的温度越高所需要的燃油量越低，燃油费也会越低。所以对于燃气轮机而言，尽可能地提高涡轮进口温度T3，是提高机组效率节约能源的有效途径。目前受材料的限制，叶片承受的温度一般不高于900 K。

1.2 叶片寿命的估计

在燃气轮机装置中，涡轮的装配叶片是需要较大规模修理和更换的结构部件。燃气轮机装置的规定寿命通常是指结构部件在经受磨损的情况下，保证结构部件可靠工作的装置持续运行时间。通常可把涡轮机组的寿命看作整个燃气轮机的设计寿命。燃气初温是影响机组寿命的关键因素。

叶片在高速旋转的燃气转子所产生的离心力和较高的燃气温度作用下，叶片金属会产生蠕变现象，当蠕变变形达到破坏极限时即会导致叶片的损伤。以额定工况为计算工况，文献[2]给出了叶片从加载到破坏的时间的近似公式

(5)

式中：T′——涡轮进口温度，T′=0.910T3；

t*——破坏时间；

σ——材料应力；

D、E——金属材料常系数。

对舰船燃气轮机，其工况通常分为部分负荷、额定负荷和超负荷三种[3]。在设计过程中通常按0.895∶0.100∶0.005的比例来分配全寿命工作时间。以t0表示额定负荷下的工作寿命，则全寿命可以表示为：

t=t0×(1-8.95+0.05)=10×t0

(6)

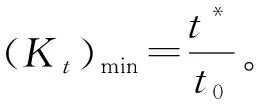
综合方程(5)、(6)及各要素可得叶片的寿命估算表达式，亦可作为机组寿命的表达式

(7)

1.3 热经济学模型

建立热经济学模型的关键是建立包含决策参数的目标函数。本文是对运行参数进行优化，故采用定投资条件下最小运行费用法建立目标函数[4]。除去与优化参数无关的运行期间的修理费、装运费、管理费等，只考虑燃料费与机组的购置费，兼顾到舰船使用功能的特定性，不考虑燃料价格的变动，以直线法计算机组折旧费，以单位小时运行成本最小为目标函数[5]，建立热经济学模型如下：

运行费用=燃料费+机组设备购置费

(8)

根据前述的热力学模型和机组寿命的表达式，设P为燃油单价，Ct为机组每小时运行所需总费用，CO为每小时燃油费，CM为机组购置费，可得目标函数

(9)

由式(9)分析可知，T3上升，CO下降，CM/t加速，反之亦然。可见，必然存在一个最佳的T3，使得Ct最小。依据数学求极值的方法，由式(9)对T3求导

可以得到最佳的T3，但式(9)是一个复杂的函数，解析法求导有一定的困难，工程上有许多数值优化方法，本文采用区间逐步分半法求解式(9)在区间[1 000，1 500]之间的极值，某点的近似导数用向后差商数值微分法求解，控制精度ε=1 K，步长h=0.5 K。程序框图如下：

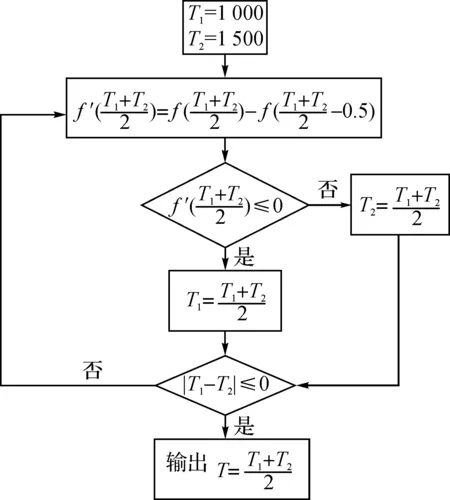
对于给定的燃气轮机，除了温度以外其余的值都可以通过查阅有关手册和燃气轮机的有关参数的说明来确定。

2 算例及分析

以GE公司的某型燃气轮机为例对其燃气初温进行优化。该型燃气轮机零配件均为国产，选取耐热钢1Cr25Ni20Si2为叶片的材料。该型燃气轮机的基本参数、有关的热力学参数和材料的参数如下：

T1=288 K；E=8.75 K;

Hμ=42 286.68 kJ/kg;σ=300 MPa;

ηe=0.7;CM=7.5×107元；

Ne=20 220 kW;Kt=20 min

D=241;P=5.0×103元/103t

说明，环境温度为初始设计温度，材料的屈服应力以及持久储备系数为权值，系数D、E相应于应力单位为MPa给出的。机组在实际循环中，存在着涡轮和压气机的内部损失，燃烧损失，工质在各流通部件内的流动损失等，用ηe表示综合考虑各因素后的总损失系数，在式(4)的分母上乘以该系数。将上述参数带入式(4)、(7)、(9)，运用MathCAD软件，得到燃气轮机的耗油率、叶片寿命和燃气轮机热经济学优化方程的函数曲线，见图2、3、4。

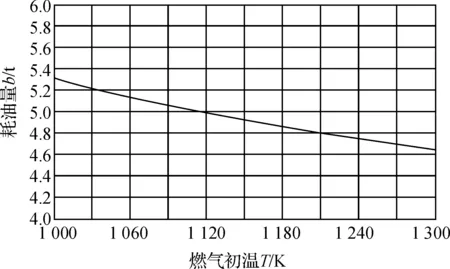
图2 燃气初温和耗油量的关系曲线

图3 燃气初温与叶片寿命的函数曲线

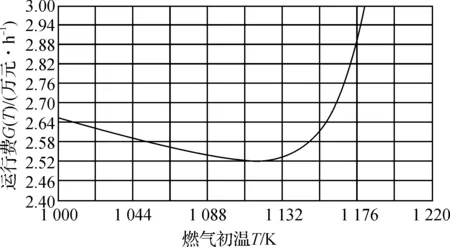
图4 热经济学优化曲线图

由图2可以很方便直观地看出燃气初温与耗油率的关系，即温度越高耗油率越低。燃气初温在1 150 ～1 250 K之间时，涡轮的入口温度为1 030～1 120 K之间，每小时耗油量在4.8 t左右，这与该燃气轮机的设计参数比较接近。

由图3，燃气初温每升高20 K涡轮叶片的寿命都将有很大的改变，特别是在1 300～1 320 K之间的时，叶片从30 000 h降到了10 000 h，超过1 340 K时，叶片寿命将迅速变为零。

图4是要得到的曲线图，从图中可以方便得找到最优化的燃气初温值，在1 100～1 150 K之间的平均消耗为2.5万元/h。燃气初温高于1 150 K或低于1 100 K时装置运行成本都将会提高。因此，这个温度区间可为机组初期设计以及机组运行期间的管理提供有益的科学指导。

3 结束语

本文以燃气轮机运行周期内每小时运行费用最小为目标函数，初步探讨了燃气轮机理想循环过程中燃气初温的优化方法。从热经济学的角度来解决节能和投资之间的矛盾，对舰船而言也就是解决舰船续航率和装备使用寿命之间的矛盾。影响燃气轮机运行的热力学参数还有环境温度，压比等因素，这些因素的影响都可应归结到温比这个参数上来，这也是燃气轮机为何设法提高材料的耐温性以提高涡轮进口温度的原因，但对应于成品机组而言选择适当的运行参数尤为重要。在此基础上也可以对其他热力学参数以及系统的设计参数作进一步优化分析。

[1] 傅秦生.能量系统的热力学分析方法[M].西安：西安交通大学出版社，2005.

[2] 刘光宇.舰船燃气轮机装置原理与设计[M].哈尔滨：哈尔滨船舶工程学院出版社,1992.

[3] 吴会泉.舰用燃气轮机装置[M].武汉：海军工程大学出版社，1992.

[4] 张晓东，王加璇，高 波.关于汽轮发电机组热经济学边际成本的研究[J].北京：中国电机工程学报，2003，23(5)：95-99.

[5] 任禾盛,王金旺，刘宝兴.微型燃气轮机热电联供系统的热经济学最优化分析[J].上海：上海理工大学学报，2005，26(5):46-49.