老师的神猜
周奕生
在一次课外活动中,老师对同学们说:“请同学们拿出一张月历,随便是哪年哪月的,然后用铅笔按我的要求圈几个数,只要告诉我这几个数的和,我就能马上猜出你们所圈的数.”
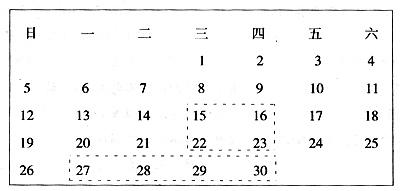
老师:请大家圈出同行连续四个数,然后告诉我这四个数的和,我马上就能知道你们圈的四个数.
小明不信老师有那么大的本事.他拿出的月历是2004年9月份的,圈出27至30这四个数,然后大声地说:“老师,我圈的四个数的和是114.”
老师:你圈的四个数是27,28,29,30.
小明:是的,您怎么这样快就知道了?
老师:这是一种“魔术”,等一下再告诉你们吧.下面再请大家任意圈出同列相邻的三个数,告诉我这三个数的和,我同样知道你们圈的三个数.
又是小明一马当先,他圈的是星期四这一列的最后三个数:“老师,我这一次圈的三个数的和是69.”
老师:你圈的三个数是16,23,30.
接着老师又说:大家用矩形任意圈出相邻两行和两列的四个数,只需告诉我这四个数的和,我同样知道你们圈的四个数.
这次是小慧眼明手快,圈出的四个数是星期三和星期四这两列中的15,16,22,23,告诉老师这四个数的和后,老师稍加思索,就说出了答案.同学们惊得目瞪口呆.
请想一想,你能揭开老师神猜的秘密吗?
其实这并不是什么魔术,而是老师掌握了月历中数的排列规律.月历中同行中的数都是连续正整数,后一个数总比前一个数大1;同列下一行的数总比上一行的数大7.你们只要记住这两点,然后再列一元一次方程,什么问题都迎刃而解.
在第一个问题中,设第一个数是x,则接下来三个数分别是x+1,x+2,x+3.已知这四个数的和是114,就得到了方程x+(x+1)+(x+2)+(x+3)=114,即4x+6=114. 解之得x=27.
你看,这四个数不就知道了吗?
原来这么简单!第二个问题与第一个问题很相似.同学们揭开了第二个问题的秘密:设第一个数是x,下一个数是x+7,再下一个数是(x+7)+7=x+14,这三个数的和为69,所以x+(x+7)+(x+14)=69,即3x+21=69,解得x=16,故三个数分别是16,23,27.
老师:请你们自己想一想,第三个问题该怎么做呢?
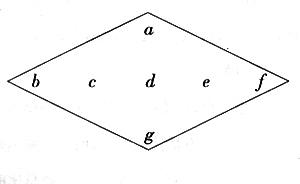
事实上,月历中还有许多规律,只要我们细心去观察,留意去思考就能够发现.比如我们可以圈出3×3,4×4这样的方阵,还可以圈出菱形阵或三角形阵等等.不论什么问题,同行或同列相邻两数的关系是月历中数的最基本特征,抓住这两个特征,什么问题都可以解决.最后请大家探索一下:月历中是否存在着如图所示的菱形阵,使得7个数的和等于140或105?若存在,请求出这7个数;若不存在,请说明理由.

