两个公平的数学游戏

陈晓兵

凡是双方对抗性的游戏，不管它的形式和内容如何，都应遵守一个重要的原则：双方获胜的机会（概率）是相等的。只有这样，才能引起游戏双方的兴趣。如果游戏的一方总是稳赢不输，或者获胜的概率远远大于失败的概率，那么这样的游戏就很难引起双方的兴趣，游戏将无法继续下去。

你见过小朋友们玩“剪刀、石头、布”的游戏吗？两个参与游戏的小朋友，同时伸出一只手，做成三种不同形状的一种：握紧拳头象征石头，伸出中指和食指象征剪刀，伸开五指一个巴掌则象征布。取胜的规则是：石头砸烂剪刀，剪刀剪碎布，布包住石头，即石头胜剪刀，剪刀胜布，布胜石头．它们循环取胜。

聪明的孩子总是不断地变换自己的手形，不让对方掌握自己出手的规律。双方如果偶然玩一两次，谁胜谁负很难预料。如果采用记分的办法：胜一次记１分，负一次记－１分，平局记０分，经过较长时间的比赛之后，你就会发现，双方的积分总是大致相当的。这说明该游戏是公平的，双方获胜的概率都是

1

—。

2

现在，我们来设计一种“猜钩”游戏的规则：

假设全桌有８人，均分为２组，每组４人，一组作藏钩者，另一组作猜钩人，藏钩的一组取两只玉钩分别藏于两人手中。然后让另一组去猜玉钩在谁的手里，每人只允许猜一个人，并且猜钩方的人事前不得有任何商量或默契。

如果有奇数个人（１个或３个）猜对了，就算猜钩的一方获胜；如果有偶数个人（无人或２人或４人）猜中了，就算藏钩的一方获胜。

在这一游戏规则下，你认为对哪一方有利一些？如果让你参加游戏，你是选择藏钩一方还是猜钩一方？

用数学方法可以证明：这样的游戏规则对双方都是公平的，哪一方也占不到便宜。

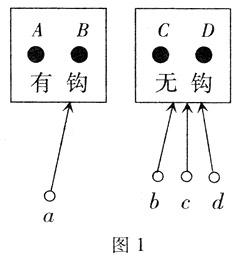
事实上，假设藏钩的一方是Ａ、Ｂ、Ｃ、Ｄ四人，猜钩的是ａ、ｂ、ｃ、ｄ四人，玉钩藏于Ａ、Ｂ二人之手，那么就把Ａ、Ｂ、Ｃ、Ｄ分成了两半，一半人（Ａ与Ｂ）手中有钩，另一半（Ｃ与Ｄ）手中无钩。猜Ａ与Ｂ这一半就能猜中，猜Ｃ与Ｄ的一半则未猜中。

猜钩的一方也总可以按所猜的情况分为两组，猜Ａ或Ｂ手中有钩（每人只允许猜一个人手中有钩）的人为一组，猜Ｃ或Ｄ手中有钩的人为另一组。根据他们所猜的情况有１６种不同的分组方式．

这些分组方式是：

无人猜中：／ａ，ｂ，ｃ，ｄ

一人猜中：ａｂ，ｃ，ｄ

ｂａ，ｃ，ｄ

ｃａ，ｂ，ｄ

ｄａ，ｂ，ｃ

二人猜中：ａ，ｂｃ，ｄ

ａ，ｃｂ，ｄ

ａ，ｄｂ，ｃ

ｂ，ｃａ，ｄ

ｂ，ｄａ，ｃ

ｃ，ｄａ，ｂ

三人猜中：ａ，ｂ，ｃｄ

ａ，ｃ，ｄｂ

ａ，ｂ，ｄｃ

ｂ，ｃ，ｄａ

四人猜中：ａ，ｂ，ｃ，ｄ／

每一个分组对应于一种猜钩方式，如图１，总共有１６组，其中使猜钩组获胜的方式共有８种，即一人猜中和三人猜中的各有４种方式。因此，猜钩组获胜的机会为

81

——=——，即获胜的机会为５０％。这说明此游戏规则对双方都是公平的。

16２

也许有人会感到奇怪，为什么你设计的这个游戏规则这么复杂呢？难道不能把规则弄得更简单一些吗？事实上，用数学方法可以证明，很难找到一种更简单的类似的猜钩规则，该规则对双方都是公平的。

现在我们来谈谈另一种“射覆”游戏。

美国电视娱乐节目主持人玛丽莲小姐曾经提出了一个“车库猜车”的游戏：

在三间彼此隔绝的车库里，有一间停有一辆汽车。请你猜一猜汽车停在哪一间车库里？

用Ａ、Ｂ、Ｃ表示这三间车库，假如你开始猜车在Ａ库里，那么不管你猜中还是没有猜中，Ｂ、Ｃ两间中总有一间是空的。这时节目主持人打开一间空车库（比方如Ｃ）告诉你，在这间车库里没有车。接下来她问你：“你是坚持原来的选择Ａ，还是重新选择Ｂ呢？要更改还来得及。”

你会怎么办呢？也许绝大多数人认为不会有差别，因为已知Ｃ库里无车，车不在Ａ库就在Ｂ库，不论选择Ａ还是选择Ｂ，猜中的可能性都是

1

—。但事实并非如此。你找一个同伴做了实验后发现，改变选择（即猜在Ｂ库）比坚

2

持原方案（即坚持猜车在Ａ库）猜中的机会要多一些。

我们在电视中常常看到一些“智力测试”的节目：主持人提出一问题，要你从四个答案中选择惟一正确的答案。如果你对答案毫无了解，只能瞎猜，靠碰运气的话，这时你可以请求主持人去掉两个不正确的答案。想想看，为了使你猜中的机会大一些，一开始你应该怎样做呢？