齿面成形方法对鼓形齿联轴器齿形及其接触性能影响机制

关键词：鼓形齿联轴器；成形方法；齿形分析；几何接触；承载接触

中图分类号：TH132 文献标志码：A 文章编号：1000-582X（2025）01-021-12

齿轮传动是制造业中多个领域的关键零部件，鼓形齿联轴器是齿轮传动不可或缺的重要组成部分。鼓形齿联轴器由一个内齿圈和一个具有相同齿数的鼓形齿轮组成，能补偿轴间角向不对中，传递扭矩大，传动性能好，在船舶[1]、交通[2]、轧钢[3]、风电[4]等领域应用广泛。

鼓形齿轮齿形为齿顶球面、齿面齿向鼓形，其齿形直接影响鼓形齿联轴器的接触性能。目前，主要有2种成形方法：方法Ⅰ为滚刀绕位移圆圆心作圆弧运动展成齿面，方法Ⅱ为插齿刀绕位移圆圆心作圆弧运动展成齿面[5]。基于方法Ⅰ，大量学者对齿面接触分析进行了研究。Alfares等[6]和魏家麒等[7]采用齿面离散网格法，研究了模数、压力角及鼓形量对间隙的影响，结果表明增大模数和压力角会增大转动过程中的最小间隙，合适的鼓形量有助于改善间隙分布。关亚彬等[8]基于接触理论，提出了一种快速精确的侧隙设计方法，并与齿面离散网格法进行了对比，验证了所提方法的精确性。陈春俊等[9]计算了高速动车鼓形齿联轴器的最小间隙，建立了运动状态与收缩电阻的关系，得出收缩电阻与力矩呈反比关系的结论。肖来元等[10-11]应用边界元对鼓形齿联轴器进行了多齿接触数值求解，得到了实际接触齿对数。Keum等[12]，Shinoda等[13-14]和Vondra等[15]采用有限元建立了轴交角下鼓形齿联轴器的有限元模型，研究了承载接触特性，最大接触应力将随着轴交角的增大出现在不同的轮齿上，接触位置从齿面的中心移动到边缘。Guo等[16]和Spura[17]分别提出了基于赫兹接触理论和Weber-Banaschek理论的鼓形齿联轴器接触解析模型，该模型可用于接触齿对数、轮齿载荷、刚度、应力、变形和安全系数的计算，与有限元方法进行了对比，验证了接触解析模型的准确性。基于方法Ⅱ，Renzo等[18]和齿轮手册[19]讨论了鼓形齿联轴器在轴交角下的运动特性和承载能力，但未给出具体建模方法。从上述分析可知，目前研究主要是基于成形方法Ⅰ进行接触分析，有关成形方法Ⅱ的研究很少。此外，成形方法Ⅰ与Ⅱ在鼓形量相等和位移圆半径相等2 种加工条件下，齿形均不相同，必然导致2 种成形方法生成的齿形及接触性能的差异。然而，成形方法对成形差异及影响机制仍不清楚。

因此，基于2种成形方法，分别建立鼓形齿轮齿面模型，采用几何和承载接触分析方法，对比了2 种成形方法在鼓形量相等和位移圆半径相等2 种加工条件下的齿形、间隙、齿间载荷分配及齿面载荷分布。齿形是影响鼓形齿联轴器接触性能的主要因素，研究以上2 种成形方法在鼓形量相等和位移圆半径相等下的接触特性，对进一步提升其性能具有重要意义。

1鼓形齿轮齿面几何模型

1.1成形方法Ⅰ

成形方法Ⅰ由滚刀绕位移圆圆心作圆弧运动展成鼓形齿轮齿面，其齿形特点是所有包含位移圆圆心的任一截面廓形与中间截面廓形相同。图1为成形法Ⅰ生成的鼓形齿轮齿面，其中图1（a）为求鼓形齿轮坐标系，以位移圆圆心O₁为原点，建立坐标系S₁（x₁，y₁，z₁），以鼓形齿轮中心点O_h为原点，建立坐标系S_h（x_h，y_h，z_h），圆心O₁到中心点O_h之间的距离用e 表示，r_a为齿顶圆半径。

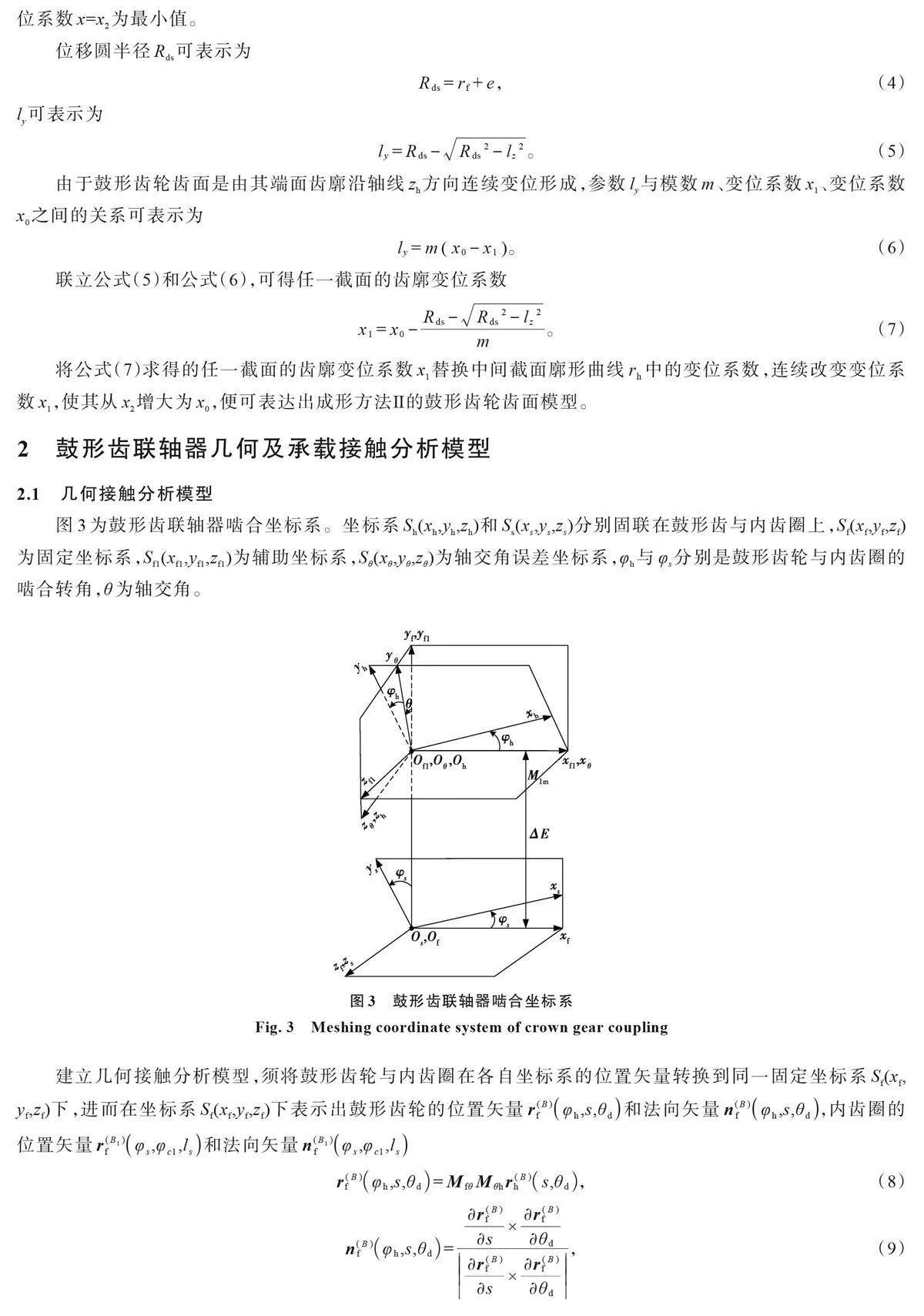
假定点M1m 为鼓形齿轮在中间截面廓形曲线r_h上的任意一点，则点M_1m 的坐标在坐标系S₁（x₁，y₁，z₁）下可表示为

式中，M_1h为坐标系S_h（x_h，y_h，z_h）到坐标系S₁（x₁，y₁，z₁）的坐标变换矩阵。

2.2承载接触分析模型

鼓形齿联轴器与一般齿轮传动[20-22]不同，在轴交角、负载扭矩下，所有齿可同时参与啮合，但所有啮合齿对的啮合状态均不相同。因此，必须建立鼓形齿联轴器的全齿有限元网格模型，研究所有啮合齿对的接触过程和应力状态的变化规律，才能反映其啮合性能，这一过程远比一般齿轮啮合分析更为复杂。

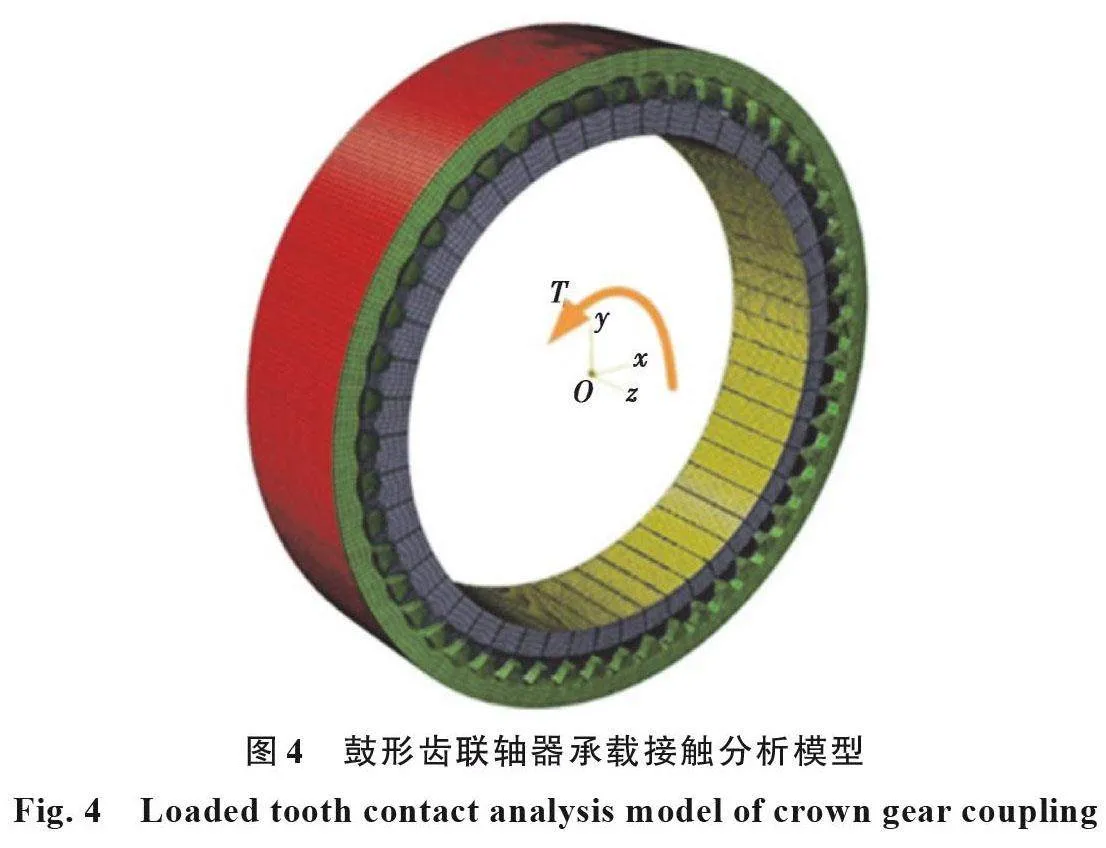
按照图3所示的啮合关系，应用空间坐标变换方法进行装配，装配后的有限元网格模型如图4 所示。在对鼓形齿联轴器进行承载接触分析时，将内齿圈轮缘节点（红色区域）施加固定位移约束，而对鼓形齿轮的约束可通过刚性耦合六自由度点单元实现。在鼓形齿轮中心参考节点（x＝0，y＝0，z＝0）定义一个单节点六自由度的点单元，将鼓形齿轮轴孔面节点（黄色区域）与该点单元刚性耦合，保留其绕z 轴的旋转自由度，其他方向的自由度全部约束，其中z 轴与鼓形齿轮轴线相同。同时，在该点单元上施加绕z 轴逆时针方向的负载扭矩T。

3位移圆半径相等下成形方法Ⅰ与Ⅱ的对比分析

以某鼓形齿联轴器为例，基于上述建立的鼓形齿轮齿面模型，深入研究位移圆半径相等下和鼓形量相等下2 种成形方法生成的鼓形齿齿形、几何接触及承载接触特性。表1为某鼓形联轴器的结构参数。

3.1齿形

位移圆半径R_ds是决定鼓形齿齿向鼓形量的重要加工参数，基于此，计算并绘制出位移圆半径R_ds分别为1000、3000、5000mm的成形方法之间的齿廓偏差分布云图，分别如图5（a）、图5（b）和图5（c）所示，图中红色、蓝色分别代表成形方法Ⅰ和成形方法Ⅱ的鼓形齿齿廓。

从图5中可以看出，在位移圆半径1000、3000、5000mm下，成形方法Ⅰ和Ⅱ的齿廓最大偏差依次为251、80、48μm。结果表明，随着位移圆半径的增大，成形方法Ⅰ和Ⅱ的齿廓形状最大偏差逐渐减小，即由2种成形方法得到的鼓形齿齿形越接近。当位移圆半径增大到无穷大时，成形方法Ⅰ和Ⅱ的鼓形齿轮齿面齿廓形状均为标准渐开线齿廓，两模型之间齿廓形状偏差均为0μm，此时成形方法Ⅰ和Ⅱ生成的齿形相同。

3.2几何接触分析

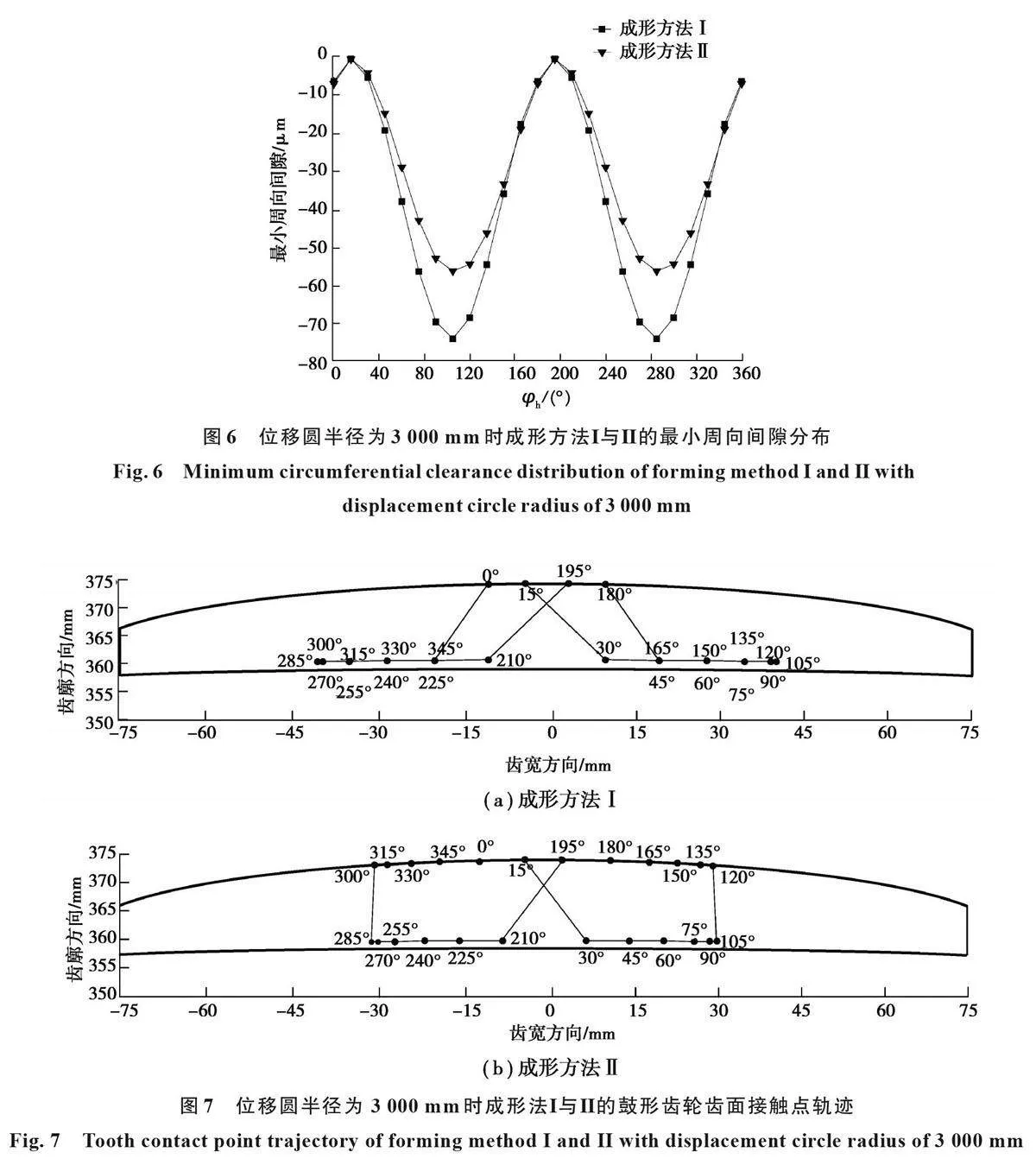
在轴交角为0.2°、位移圆半径为3000mm时，应用提出的几何接触分析模型[23]，求解出成形方法Ⅰ与Ⅱ的鼓形齿联轴器最小周向间隙分布及齿面接触点轨迹，如图6和图7所示。

从图6中可以看出，对于成形方法Ⅰ与Ⅱ，从初始啮合转角0°开始，转动1 周至啮合转角360°的过程中，最小周向间隙均按照啮合转角在0°～15°逐渐增大，15°～105°逐渐减小，105°～195°逐渐增大，195°～285°逐渐减小，285°～360°逐渐增大的规律变化并且呈现周期性变化。成形方法Ⅰ与Ⅱ的最小周向间隙在纯摆动区附近（φh=15°和195°）达到最大，均为0μm；在纯翻转区附近（φh=105°和285°）达到最小，分别为-74μm和-56μm。因此，当鼓形齿联轴器轴线角向不对中时，成形方法Ⅰ的最小周向间隙的最小值比成形方法Ⅱ的小。

从图7中可以看出，成形方法Ⅰ与Ⅱ在每一个啮合转角（0°～360°）处鼓形齿轮和内齿圈呈点接触，接触点沿齿廓方向分布在鼓形齿的齿顶和齿根区域，纯摆动区域附近的接触点靠近齿宽中间截面，而纯翻转区附近的接触点靠近齿宽端部。对比成形方法Ⅰ与Ⅱ，发现成形方法Ⅰ大多数的接触点都处于鼓形齿轮齿面的齿根处，而成形方法Ⅱ的接触点在鼓形齿轮齿面的齿根处和齿顶处的数目基本一致。

3.3承载接触分析

在轴交角为0.2°、负载为1.75×10⁶N·m时、位移圆半径为3000mm 时，应用承载接触分析模型，对比分析成形方法Ⅰ与Ⅱ的承载接触特性。

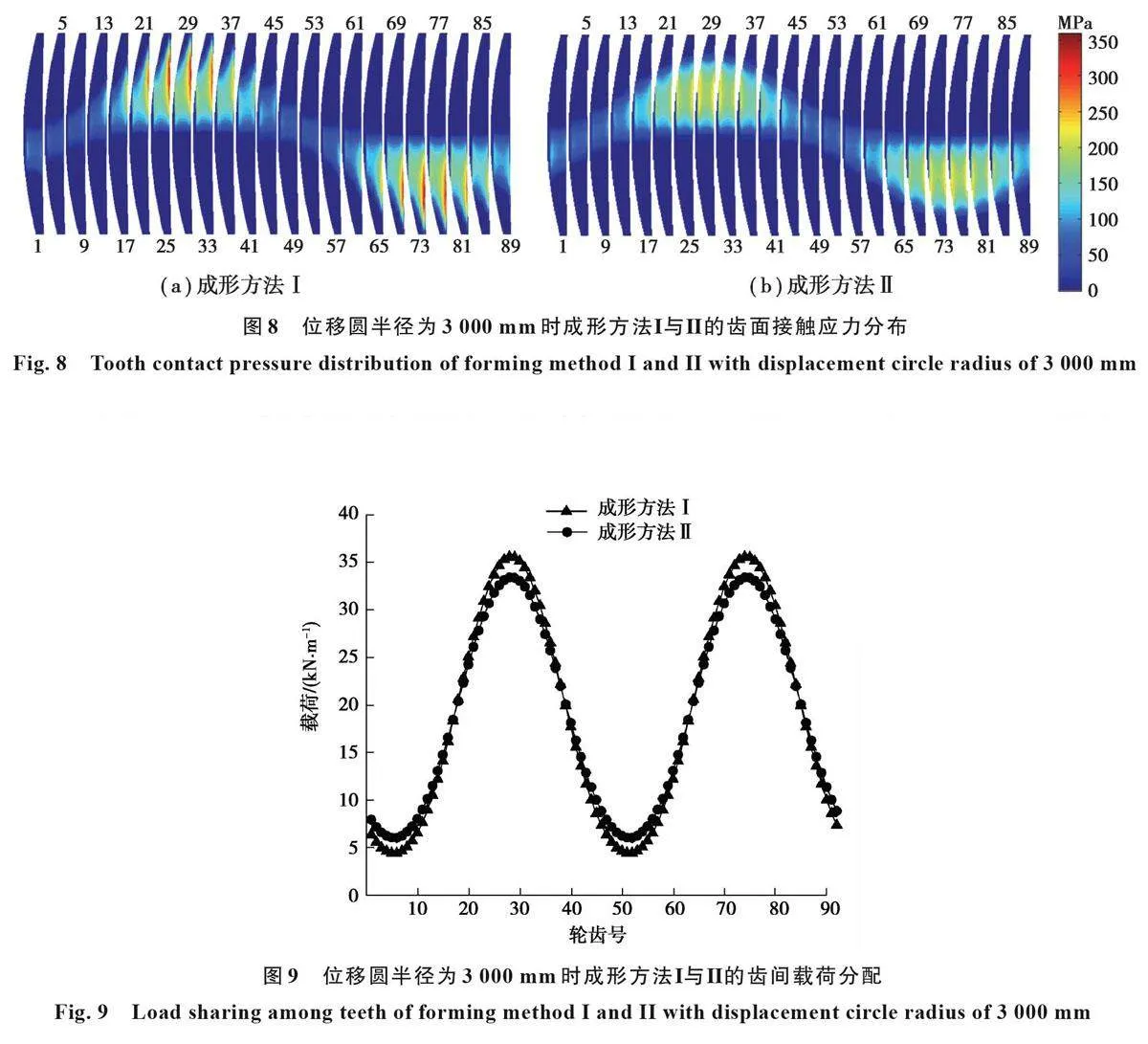
图8为成形方法Ⅰ与Ⅱ的齿面接触应力分布。从图中可以看出，当鼓形齿轮与内齿圈由轴向对中转为轴线角向不对中时，接触位置由齿宽中间截面向端面移动，此时并非所有轮齿都参与啮合，而是只有部分纯翻转区附近的轮齿处于接触状态。与成形方法Ⅱ相比，成形方法Ⅰ会引起更加严重的应力集中，产生更大的齿面接触应力。成形方法Ⅰ与Ⅱ的最大齿面接触应力分别为359MPa和270MPa，成形方法Ⅰ的最大接触应力比成形方法Ⅱ大33%。

图9为成形方法Ⅰ与Ⅱ的齿间载荷分配曲线。从图中可以看出，成形方法Ⅰ与Ⅱ参与啮合的齿对数均为92，受到载荷最大轮齿位置处于纯翻转区附近的轮齿#29、#75，受到的载荷依次为35579、33401 N·m。受到载荷最小轮齿位置处于纯摆动区附近的轮齿#5、#51，受到的载荷依次为4432、6060 N·m。最大受载轮齿比最小受载轮齿承受的载荷多702.8%、451.2%。因此，在相同的位移圆半径下，成形方法Ⅱ比Ⅰ的齿间载荷分配更加均匀。

4鼓形量相等下成形方法Ⅰ与Ⅱ的对比分析

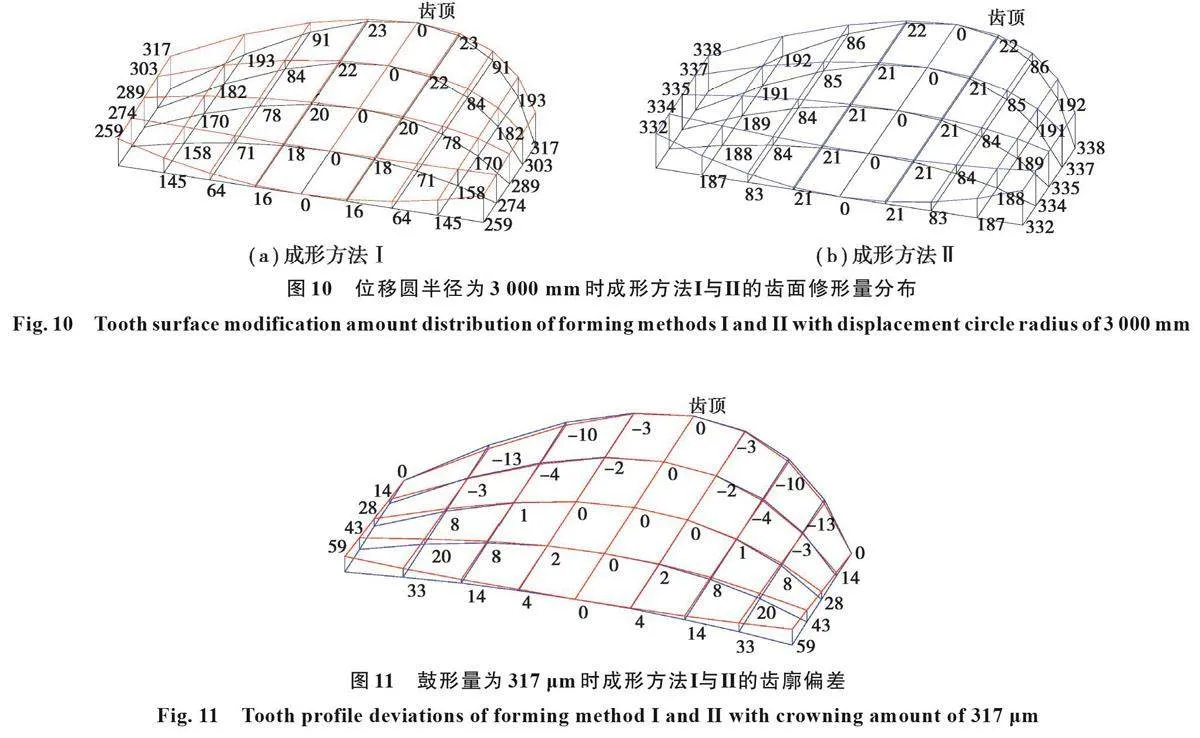
图10（a）和10（b）分别为位移圆半径3000mm时成形方法Ⅰ与Ⅱ的鼓形齿相对于标准直齿轮的齿面修形量分布，其图中红色、蓝色、黑色分别代表成形方法Ⅰ的鼓形齿齿廓、成形方法Ⅱ的鼓形齿齿廓及标准直齿轮齿廓。从图10（a）可以看出，在位移圆半径3000mm时，成形方法Ⅰ与Ⅱ的鼓形量（即图中的最大修形量）分别为317μm 和338μm，可知成形方法Ⅱ在相等位移圆半径下鼓形量并不相等。本节将对鼓形量相等下成形方法Ⅰ与Ⅱ在齿形、几何接触特性和承载接触特性等方面进行对比分析。为保证成形方法Ⅰ与Ⅱ的鼓形量相等，须改变其中任一成形方法的位移圆半径。成形方法Ⅰ在位移圆半径3000mm 时的鼓形量为317μm，要使成形方法Ⅱ的鼓形量与成形方法Ⅰ相等，成形方法Ⅱ的位移圆半径须增大为3200mm。

4.1齿形

图11为鼓形量为317μm时成形方法Ⅰ与Ⅱ的齿廓偏差，其图中红色、蓝色分别代表成形方法Ⅰ和成形方法Ⅱ的鼓形齿齿廓。从图中可以看出，齿廓偏差在齿端靠近齿根达到最大值59μm。齿廓偏差在齿端靠近齿顶为0μm，这是由于成形方法Ⅰ和Ⅱ生成的鼓形齿轮齿面修形量均在此处最大。此外，齿廓偏差仍关于齿宽中间截面对称。

4.2几何接触分析

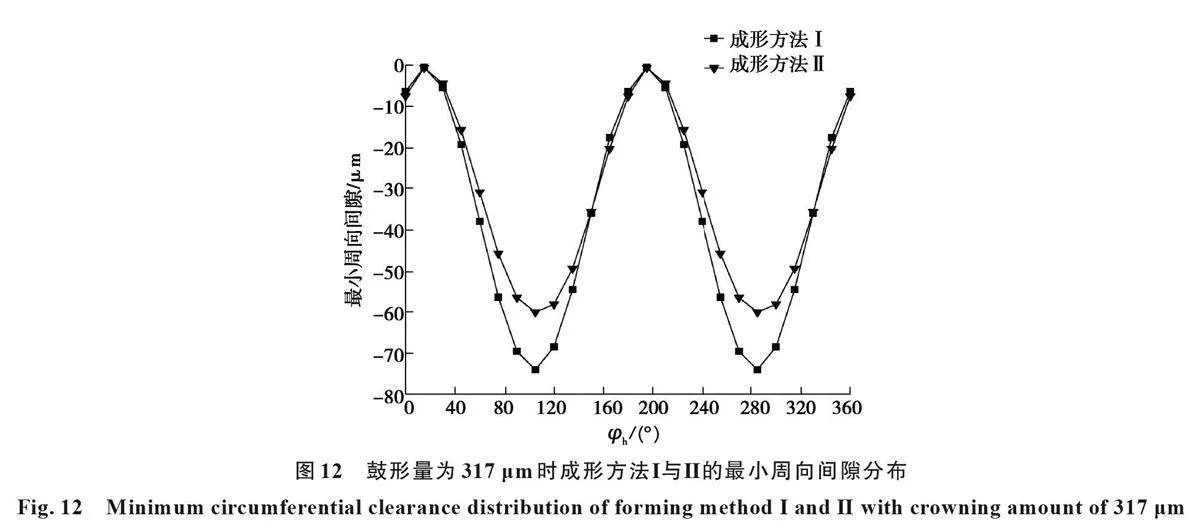
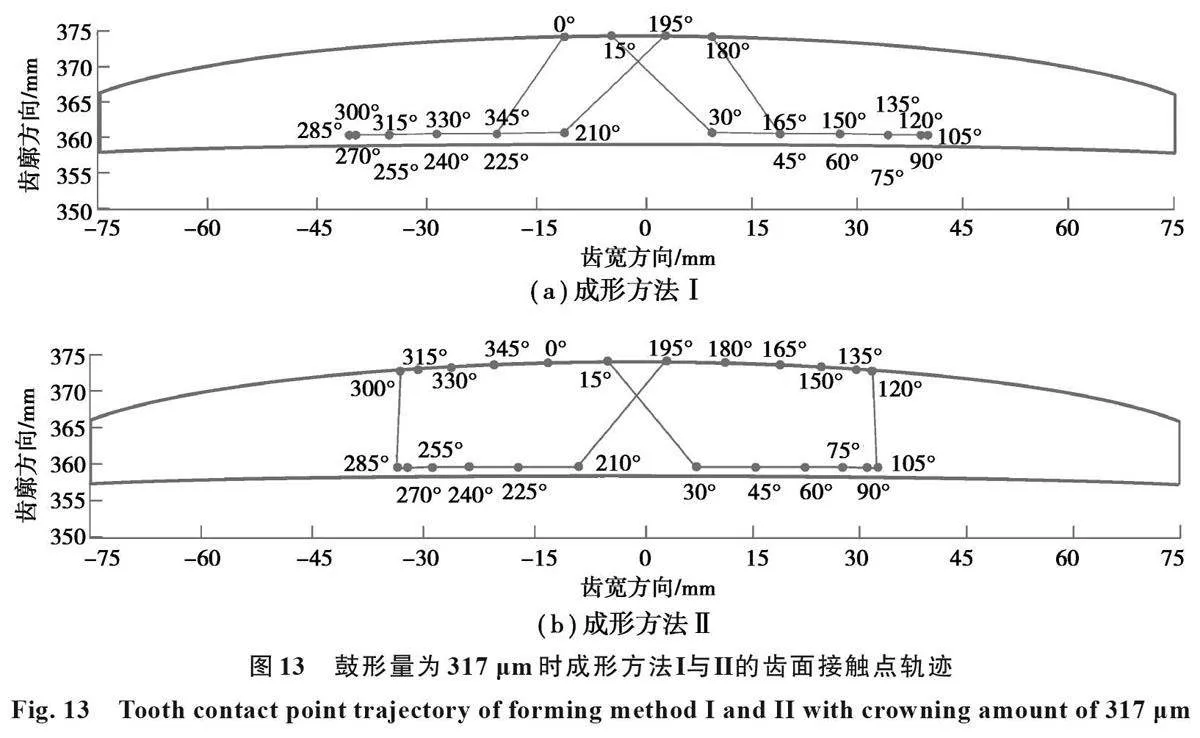
在轴交角为0.2°、鼓形量为317μm时，应用几何接触分析模型，求解出成形方法Ⅰ与Ⅱ的最小周向间隙分布及齿面接触点轨迹，如图12和图13所示。

从图12中可以看出，成形方法Ⅰ与Ⅱ的最小周向间隙在纯摆动区附近（φ_h为15°和195°）达到最大，均为0μm；在纯翻转区附近（φ_h为105°和285°）达到最小，分别为-74μm 和-60μm。因此，在鼓形量相同、轴线角向不对中下，成形方法Ⅰ的最小周向间隙的最小值比Ⅱ小。

对比图13（a）和图13（b）可以发现，成形方法Ⅰ的大多数的接触点都处于鼓形齿轮齿面的齿根，而成形方法Ⅱ的接触点在鼓形齿轮齿面的齿根处和齿顶处的数目基本一致。对比图13（b）和图7（b）可以发现，鼓形量相等下成形方法Ⅱ的接触点轨迹比位移圆半径相等下成形方法Ⅱ的接触点轨迹向齿宽端部略有扩展，这是由于鼓形量相等下的成形方法Ⅱ位移圆半径比位移圆相等下成形方法Ⅱ位移圆半径大，对轴交角更敏感。

4.3承载接触分析

在轴交角为0.2°、负载为1.75×10⁶N·m、鼓形量为317μm时，应用承载接触分析模型，对比分析成形方法Ⅰ与Ⅱ的承载接触特性。

图14为成形方法Ⅰ与Ⅱ的齿面接触应力分布。对比图14（a）和图14（b）可以看出，在鼓形量相等下，成形方法Ⅱ在纯翻转区附近的轮齿在齿顶和齿根处均存在边缘接触，而成形方法Ⅰ在纯翻转区附近的轮齿仅在齿根处存在边缘接触。

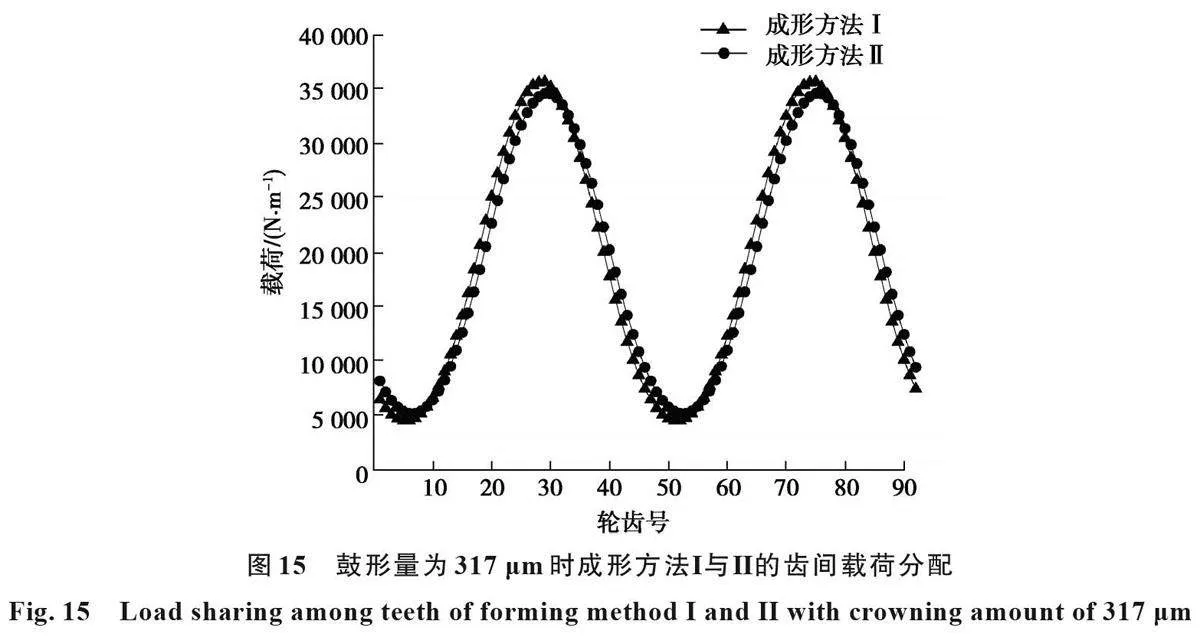
图15为成形方法Ⅰ与Ⅱ的齿间载荷分配曲线。对比图15和图9可以发现，鼓形量相等时，两模型的齿间载荷分配曲线比位移半径相等时更接近。因此，在轴交角和负载扭矩一定的条件下，齿面的鼓形量决定了鼓形齿联轴器的齿间载荷分配曲线。

5结论

为揭示成形方法生成的鼓形齿轮齿形差异及影响机制，分别建立了滚刀和插齿刀绕位移圆圆心作圆弧运动展成的鼓形齿轮齿面模型。在此基础上，对比分析了成形方法Ⅰ与Ⅱ分别在位移圆半径相等时和鼓形量相等时的齿形、几何接触特性、承载接触特性，得出了以下结论。

1）成形方法Ⅰ与Ⅱ在位移圆半径相等时，随着位移圆半径的增大，成形方法Ⅰ与Ⅱ的齿形最大偏差逐渐减小；成形方法Ⅱ比Ⅰ的齿间载荷分配更加均匀。

2）成形方法Ⅰ与Ⅱ在鼓形量相等时，成形方法Ⅱ的位移圆半径须大于模型Ⅰ；成形方法Ⅰ与Ⅱ的齿间载荷分配非常接近。

3）鼓形量相等时成形方法Ⅱ的接触点轨迹比位移圆半径相等时成形方法Ⅱ的接触点轨迹更靠近齿端。

4）不论在位移圆半径相等时，还是在鼓形量相等时，成形方法Ⅰ的最小周向间隙小于成形方法Ⅱ；成形方法Ⅰ的接触点大多数位于鼓形齿轮齿根处，成形方法Ⅱ的接触点均位于齿顶或齿根；成形方法Ⅰ比Ⅱ会产生更加严重的应力集中。