点蚀故障下行星齿轮传动振动特性

关键词：行星齿轮传动；点蚀；振动特性；时频响应

中图分类号：TH113.1 文献标志码：A 文章编号：1000-582X（2025）01-010-11

点蚀是齿轮传动系统中最普遍的失效形式，在齿轮传动过程中，每个齿面在经历循环变化的接触应力后，齿轮表面或亚表面会出现大小不同的微裂纹，随着齿轮工作时间的增加，齿面金属脱落，形成巨点蚀。当齿轮齿面出现点蚀失效时，齿轮箱内部激励发生改变，从而影响整个系统的动力学特性，同时影响齿轮箱甚至传动系统的可靠性与稳定性。

关于齿轮点蚀国内外学者进行了较多的研究。Choy等[1]通过齿轮啮合刚度的相位和幅值变化来模拟齿轮表面点蚀和磨损的影响。Lin等[2]提出了一种试验前用轮廓测量仪测量齿轮轮廓的齿轮点蚀磨损测量方法。 Liang 等[3]揭示了点蚀故障现象，并考虑了齿面上的点蚀扩展对时变啮合刚度的影响，从而导致动态响应的变化。Wei 等[4]考虑局部微凸体摩擦引起的高剪切力，研究了微点蚀、点蚀顺序的形成。李金锴等[5]基于有限元的斜齿轮啮合刚度计算方法建立正常和疲劳点蚀斜齿轮，分析了点蚀长度和宽度对啮合刚度的影响，通过试验验证齿轮啮合刚度的减小使得齿轮振动冲击响应增大，结果表明剥落长度会影响齿轮啮合刚度的变化区域。Luo 等[6]考虑了由于点蚀和剥落引起的齿面粗糙度变化等因素，提出了一种新的直齿轮动力学模型。Ma 等[7]通过对不同点蚀宽度、长度和位置下的损伤程度进行比较，结果表明：随着点蚀宽度的增加，齿轮啮合刚度急剧下降，其中单齿啮合时最为明显。冯淦淇等[8]针对齿轮点蚀故障特征难以提取的问题，提出了一种基于改进变分模态分解的齿轮点蚀故障诊断方法。Kundu 等[9]提出了一种二元分割方法，该方法可以基于健康模型振动信号，识别齿轮自然点蚀过程中的3 种不同齿轮点蚀复杂程度。杨青乐等[10]基于小波变换方法提出了一种极坐标增强的方法，该方法能够有效诊断出齿轮早期微点蚀故障。Elasha 等[11]采用多种不同的振动分析技术评估了3 种齿轮箱齿轮点蚀的状况。Li 等[12]提出了一种物理模型预测在复合润滑条件下渐开线齿轮齿面微小点蚀的发展变化情况。陈勇等[13]通过冲击函数法，接触线百分比法和齿轮系统动力学理论，建立了不同点蚀类型的斜齿轮系统动力学模型，分析了点蚀斜齿轮系统的动态响应。Li 等[14]基于单级齿轮副的动力学方程，分别分析了健康状态下齿轮副和不同故障下齿轮副的频率响应。王雄等[15]基于临界平面法多轴疲劳寿命预测模型，采用临界平面方法计算SWT（Smith-Watson-Topper）参数和最易萌生裂纹的平面，最终确定齿轮疲劳点蚀寿命，并实验验证模型有效性。

现有研究多以平行级齿轮传动为研究对象，涉及行星齿轮的点蚀研究和对行星齿轮点蚀系统动力学特性的研究较少，大多缺乏试验对模型的验证。笔者建立了不同点蚀故障情况行星齿轮柔性多体动力学模型，分析了整个行星齿轮的振动响应，搭建行星齿轮点蚀试验台架，对比分析不同循环次数下点蚀形貌的演化过程和齿面不同点蚀情况对行星齿轮振动响应的影响，并验证动力学仿真模型的准确性。

1行星齿轮点蚀动力学建模

1.1行星齿轮点蚀动力学模型参数

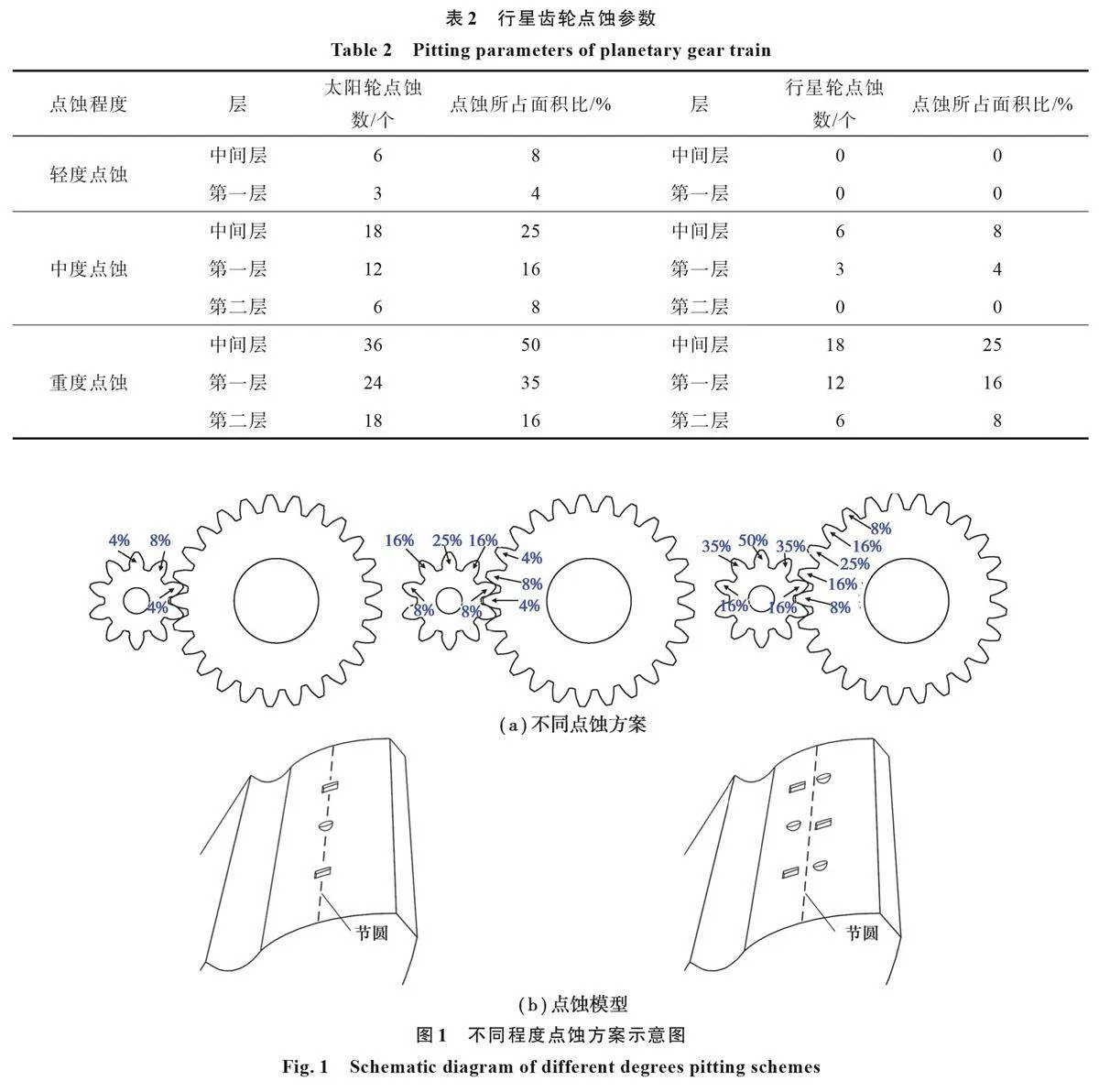
文中以某直齿行星齿轮为研究对象，主要参数如表1 所示。研究过程中，假设太阳轮与行星轮均可能发生点蚀。所有的预制点蚀均设置在轮齿节线附近，建立3 种点蚀故障程度依次递增的齿轮模型，分别为：轻度点蚀、中度点蚀和重度点蚀模型。其中不同之处在于太阳轮与行星轮齿面的点蚀数目和点蚀面积所占齿面面积比不同，如表2所示，其中点蚀坑形状为矩形和圆球的一部分混合。不同程度点蚀方案示意图如图1所示。

1.3行星齿轮耦合动力学模型

行星齿轮材料为20CrMnTi，弹性模量为2.06×10⁵MPa，密度为7 870 kg∙m^-3，泊松比为0.3。根据每个零部件之间的运动关系，在ADAMS 动力学分析软件中分别在各部件创建柔性多点约束（multipointconstraint， MPC）。在轮齿的节圆附近依次创建3个柔性MPC，均匀分布在齿宽方向。通过旋转副、接触设置对行星齿轮进行相关约束，根据材料特性对接触力进行设置。Step（time， 0， 0 d， 0.1，7200d）为文中施加转速方程，即time 为0～0.1s时，转速从0 （°）/s 增至7200 （°）/s。本模型与试验相对应，内齿圈固定，太阳轮为输入端。行星齿轮多柔体动力学模型如图2所示。

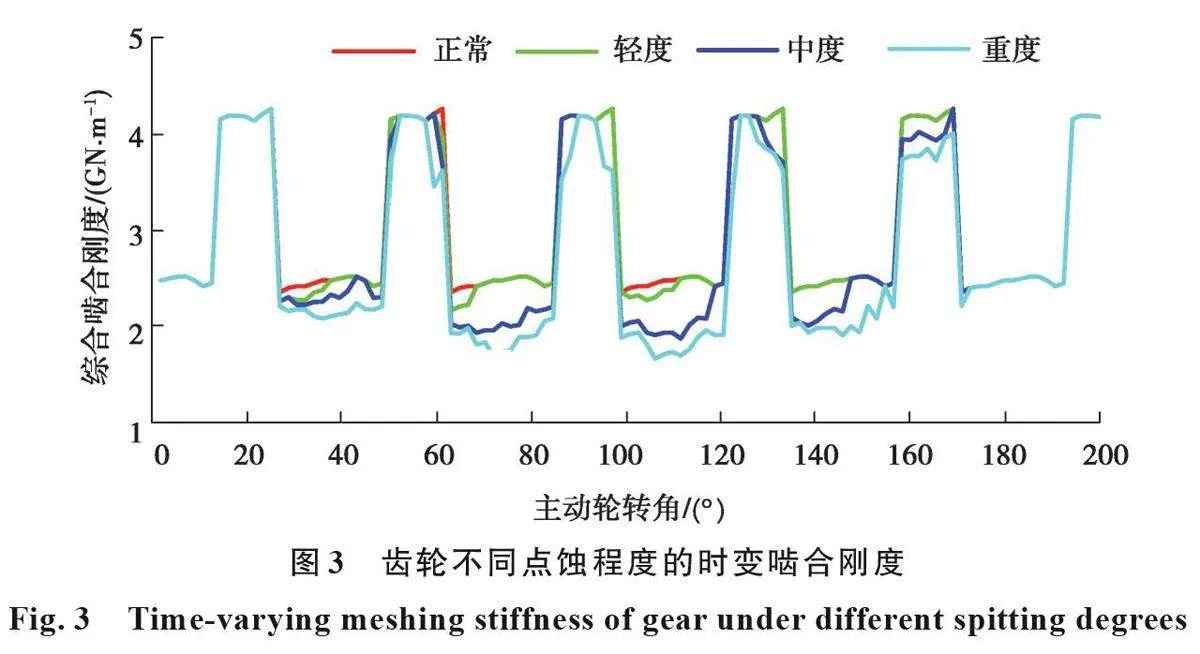
行星齿轮不同点蚀程度的时变啮合刚度如图3所示，当齿轮接触区域进入点蚀区域时，正常齿轮综合啮合刚度平稳。轻度点蚀齿轮齿面剥落较少，啮合刚度相比正常齿轮啮合刚度略有下降，出现少量冲击；中度与重度点蚀齿轮由于点蚀数量和大面积点蚀剥落，综合啮合刚度相比正常齿轮下降较多，且刚度曲线波动较大，受到了较大冲击。

随着点蚀面积的不断增大，齿轮副的综合啮合刚度逐渐减小。点蚀的位置一般偏低，当齿轮进入双齿啮合区时，主从动轮的接触位置离节线较远，此区域点蚀分布稀少，对啮合刚度的影响也较小，综合时变啮合刚度在单齿啮合区比双齿啮合区下降得快；而当轮齿进入单齿啮合区时，主从动轮接触位置位于节线下部分，正逐渐往节线靠拢，节线附近的点蚀分布密集，对啮合刚度的影响较大。

2不同点蚀模型动态响应分析

2.1时域分析

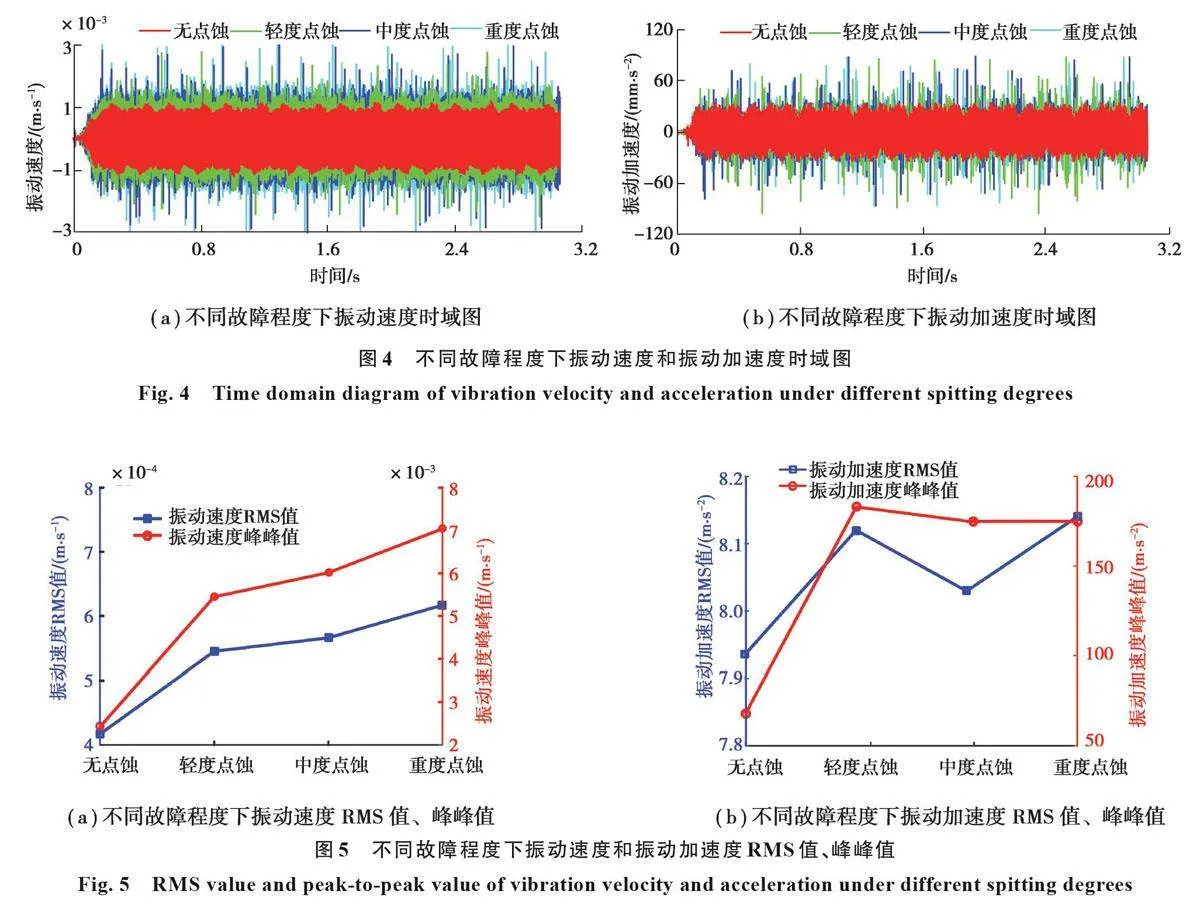
以X方向为研究对象（方向如图2所示），不同点蚀情况下行星齿轮振动速度和振动加速度时域图如图4所示。正常齿轮振动速度分布均匀，幅值稳定。轻度点蚀齿轮振动速度相对于正常齿轮幅值出现了轻微突变和周期性变化。中度和重度点蚀齿轮振动速度幅值明显增大并伴随周期性的冲击。从振动加速度时域图可以看出正常齿轮振动加速度幅值平稳、无冲击。而轻度、中度、重度点蚀齿轮振动加速度在幅值上比正常齿轮有较大的增加。不同点蚀情况下的振动速度和加速度RMS（root mean squre）值、峰峰值可知，轻度、中度和重度点蚀模型的振动速度RMS值相较于无点蚀模型分别增加了31%、35% 和48%，振动速度峰峰值相分别增加了126%、149%和192%，如图5 所示。行星齿轮振动速度RMS和峰峰值随着点蚀的复杂程度增加而呈现增加趋势，行星齿轮振动响应更加恶劣，同时不同点蚀情况给行星齿轮振动加速度造成了不规律的冲击。振动加速RMS值、峰峰值和齿轮点蚀程度并未呈现出明显规律。

2.2频域分析

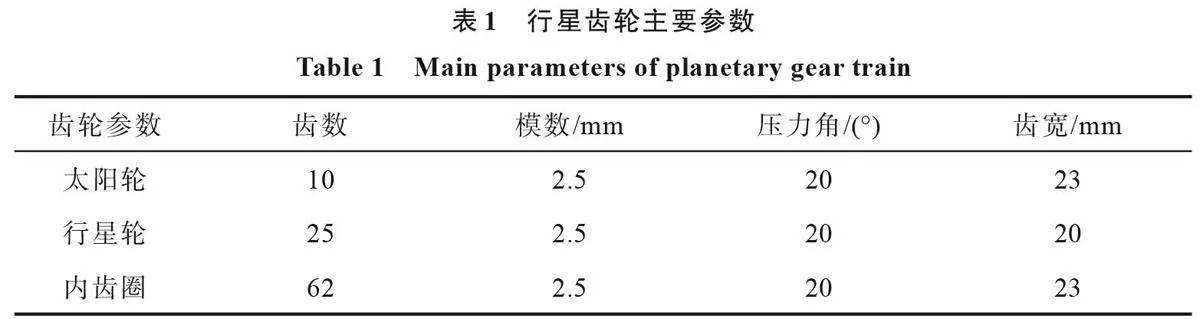
对时域信号进行傅里叶变换得到频域信号，振动速度和加速度频域信号如图6所示。从频域方面分别分析齿轮系统振动速度和振动加速度，最高频率截至8倍啮合频率，其中f_m为齿轮的啮合频率，nf_m为齿轮的n倍啮合频率。

由图6中不同点蚀故障振动速度频域图可以看出，无点蚀模型振动速度频域信号中主要包含齿轮啮合频率f_m及其倍频。轻度点蚀齿轮振动速度频域图中，整体幅值相比无点蚀模型有所增加，在啮合频率及其倍频附近出现相对少量幅值较低的边频信号。中度及重度点蚀齿轮振动速度频域图中2f_m、3f_m啮合频率幅值比轻度点蚀齿轮有所增加，同样在啮合频率及其倍频附近产生明显的边频带，且幅值更为明显。在所有频率成分中，f_m～5f_m的频率幅值最小值均在无点蚀模型中产生，6f_m～8f_m频率幅值变化并无规律。

由图6 中不同点蚀故障振动加速度频域图可以看出，无点蚀模型振动加速度频域信号中主要包含齿轮啮合频率fm 及其倍频。轻度点蚀齿轮振动加速度啮合频率及其倍频附近出现少量幅值较低的边频信号。中度、重度点蚀齿轮振动加速度同样在啮合频率及其倍频附近产生明显的边频带，幅值更为明显。高倍啮合频率（4f_m、5f_m、8f_m）幅值均随着点蚀严重程度的增加而出现明显下降。振动加速度频域信号在有点蚀模型啮合频率及其倍频附近出现边频带。

综上可知，当行星齿轮箱发生点蚀故障时，主要体现出以下2种特性：

1）冲击特性。当齿轮表面出现点蚀凹坑时，由于齿轮接触面不平整而出现冲击激励，反映到振动信号时域中，即振动信号出现峰值；在频域上，即齿轮特征频率边频带的增加。

2）周期特性。当齿轮表面出现点蚀凹坑时，所在齿每参与一次啮合就会产生一次故障激励，其出现的频率不仅与齿轮的转速有关，还与相互啮合的齿轮齿数和点蚀的齿数有关，因此随着点蚀复杂程度的增加，其频率也会发生相应变化。

3行星齿轮疲劳点蚀试验分析

3.1试验设计

为验证所建立的不同点蚀情况行星齿轮振动响应结果的正确性，建立如图7（a）所示的行星齿轮传动点蚀故障试验台开展研究。行星齿轮试验件参数与仿真参数相同。测试工具主要有三向加速度传感、DASP测试系统和相应连接数据线。行星齿轮试验件如图7（b）（e）所示，润滑油为长城6 号液力传动润滑油。采用如图7（c）所示的三维超景深显微镜测量齿轮齿面点蚀形貌，齿面粗糙度测量采用如图7（d）所示的白光干涉仪。在输入和输出位置分别布置三向传感器。

3.2形貌测量结果分析

对轮齿初始表面形貌和初始表面粗糙度进行测量，结果如图8所示。输入转速为277.77r/min，负载扭矩为1728N·m。行星齿轮在试验工况下运行6×10⁵转后轮齿表面形貌如图9所示，试验过程中首先出现的是齿顶附近的轻微磨擦磨损现象。节圆附近出现了大量鱼鳞状的波纹和少许表面裂纹。

选取如图10所示的3个点蚀坑进行追踪测量。在试验工况下运行1.2×10⁶转后，轮齿表面微点蚀坑形貌如图10所示。在转动过程中出现的大量点蚀坑可以按照深度分为小于50μm的微点蚀坑和大于50μm的巨点蚀坑。整体来看，点蚀坑表面以圆形和矩形为主，微点蚀坑1～3的夹角均为20°～50°，深度不大于22μm。

运行2.4×10⁶转后，第二阶段的巨点蚀坑与第一阶段的微点蚀坑形貌有些许不同。巨点蚀坑深度多在59 μm 以上，1号点蚀坑深度增加了47.67μm，2号点蚀坑深度增加了62.04μm，3号点蚀坑深度增加了104.76μm，其中最大深度达到了126μm，夹角大多为45°左右。随着循环次数的增加，微点蚀凹坑边沿的应力大于齿面其余区域应力，这将导致新微裂纹的产生，微裂纹又在循环应力的作用下形成新的微点蚀，新旧微点蚀之间相互合并贯通，最终逐渐演变为巨点蚀坑。另外，在齿宽方向最外端的点蚀发展较快，最先出现肉眼可见的巨点蚀。

运转4.8×10⁶转后，相比于第二阶段1号点蚀坑的深度增加了3.79μm，2号点蚀坑的深度增加了3.52 μm，3号点蚀坑的深度增加了11.2μm，其中最大深度达到了137.3μm，夹角同样大多为45°左右。

试验结果表明：由微点蚀生长为巨点蚀的过程中，深度和宽度的变化均较大，而巨点蚀继续生长的过程中，深度和宽度方向的变化均会放缓。

3.3试验结果分析

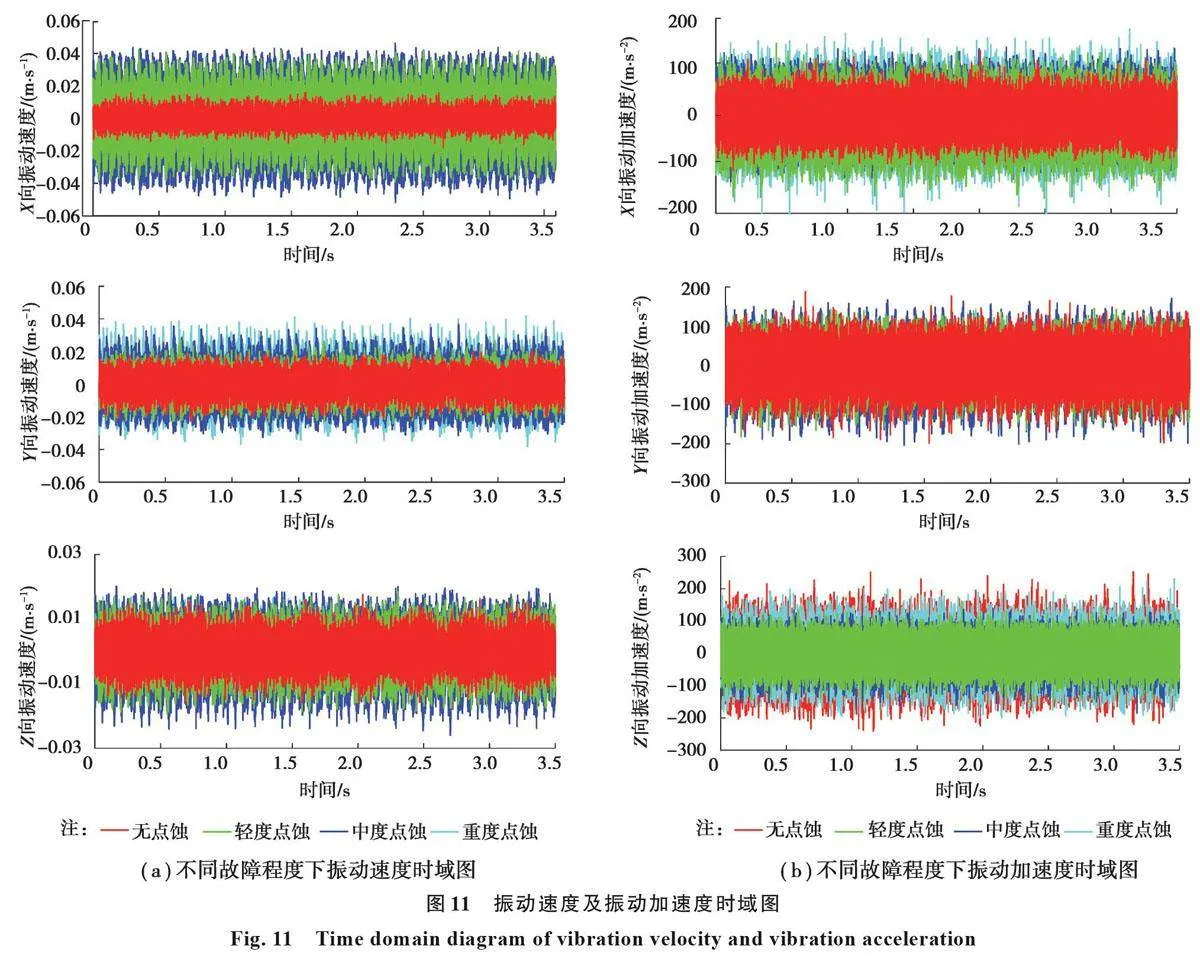
不同点蚀情况行星齿轮振动速度和加速度时域信号如图11所示。X向振动速度中，无点蚀齿轮振动速度稳定，波动值较小，无冲击，轻度、中度点蚀齿轮振动速度幅值出现周期性峰值，振动速度峰值相比无点蚀齿轮大2～3倍，但重度点蚀振动速度值低于轻度点蚀。试验中Y方向（方向如图7（a）中所示）对应仿真模型中的X方向，其Y向振动速度中，无点蚀模型振动速度信号稳定，峰值波动不大，可以看出轻度、中度、重度点蚀模型振动速度出现周期性变化和冲击，并且幅值呈递增趋势。Z向振动速度中，4种模型振动速度均出现周期性变化的峰值幅值，大小并没有明显的差别。

不同点蚀情况行星齿轮振动加速度时域信号3个方向上均出现了峰值周期性的变化，幅值上并未呈现任何规律。

不同点蚀情况行星齿轮振动速度RMS 值与峰峰值如图12所示，Y向振动速度RMS值和峰峰值均随着点蚀复杂程度的增加而呈现递增规律，与仿真结果相符。其中轻度、中度和重度点蚀模型的振动速度RMS值比无点蚀模型分别增加了13%、98%和106%；振动速度峰峰值比无点蚀模型分别增加了23%、63%和90%。仿真中X 向轻度、中度和重度点蚀模型的振动速度RMS值比无点蚀模型分别增加了31%、35%和48%；峰峰值比无点蚀模型分别增加了126%、149%和192%，试验结果趋势与仿真相符。

不同点蚀情况行星齿轮振动加速度RMS值与峰峰值如图13所示，对比不同模型在不同方向的振动加速度RMS值和峰峰值可知，行星齿轮箱3个方向的振动加速度RMS值和峰峰值随着点蚀复杂程度的增加并没有呈现出明显规律，试验结果与仿真结果基本相符。

4结论

文中以行星齿轮为研究对象，建立了不同点蚀故障下的行星齿轮模型，对其振动特性进行研究，并通过试验研究进行对比，结论如下：

1）仿真中X方向与试验中Y方向对应，振动速度RMS值和峰峰值均随着点蚀复杂程度的增加而增加，而振动加速度无明显规律。

2）振动速度2f_m、3f_m啮合频率值随点蚀严重程度增加而增加；振动加速度4f_m、5f_m、8f_m幅值随点蚀严重程度增加而下降。有点蚀模型中振动速度和振动加速度在啮合频率周围出现明显的边频带。

3）微点蚀生长为巨点蚀的过程中，深度和宽度的变化均较大，而巨点蚀继续生长的过程中，深度和宽度方向的变化均会放缓。