求解高光谱解混的三算子分裂方法

摘要： 对于高光谱解混问题，提出了一个相应的三算子单调包含和求解该问题的一个分裂方法，其中邻近因子可以自适应选取。该方法还可用于求解更一般的带有线性复合的三算子单调包含问题。数值实验表明，该算法的性能远远超过最近提出的邻近内点方法，并且与其变尺度版本相当。

关键词： 邻近内点法； 单调包含； 分裂方法； 高光谱解混； 自适应

中图分类号： O221.2

文献标志码： A

文章编号： 1671-6841（2025）02-0085-04

DOI： 10.13705/j.issn.1671-6841.2023172

A Three-operator Splitting Method for Solving Hyperspectral Unmixing

DONG Yunda， ZHANG Yuanyuan， LI Yiyi

（School of Mathematics and Statistics， Zhengzhou University， Zhengzhou 450001， China）

Abstract： We propose A three-operator monotone inclusion for hyperspectral unmixing was proposed and a corresponding splitting algorithm was given in which proximal factors could be selected adaptively. The algorithm could be also used to solve more general three-operator monotone inclusion with one linear composition. Numerical experiments showed that the algorithm outperformed the recently proposed proximal interior point algorithm and was comparable to its variable metric version.

Key words： proximal interior point algorithm; monotone inclusion; splitting method; hyperspectral unmixing; self-adaption

0 引言

高光谱解混（hyperspectral unmixing）就是将传感器获取的混合像元的光谱分解为不同纯地物的光谱以及估计其相应的比例。文献［1］提出了一个高效的数值解法——邻近内点算法（proximal interior point algorithm，PIPA）。该算法的外迭代是内点法，而内迭代是运用向前、向后分裂算法来求解子问题。

本文则将内迭代中的子问题转化为三算子单调包含，并运用文献［2］中的方法来求解。

1 问题描述

设s和r分别是获得图像的光谱带数和像素数，q是材料（端元）的个数。我们使用式（1）线性模型来关联数据、端元和丰度，

Y=SX+ω，（1）

其中：Y=R^s×r表示测得的高光谱立方体；S∈R^s×q是一个已知的数据库，它的每一列都对应着预计会出现在场景中的一种材料（或端元）的光谱；

X∈R^q×r表示丰度矩阵，它用来描述每种材料（或端元）在每个像素中的比例或丰度；ω代表加性白噪声。

更为具体的，我们依据文献［1］将高光谱解混转化为约束极小化问题，

minX∈R^q×r

12‖Y-SX‖2F+σ∑qi=1‖（WXi）d‖1，

s.t. ∑qi=1Xi，j≤1，j∈｛1，…，r}，

Xi，j≥0，i∈｛1，…，q}，j∈｛1，…，r}，（2）

其中：‖·‖F是Frobenius范数;Xi∈Rr，i∈｛1，…，q}代表丰度矩阵的第i行;

W∈R^r×r表示小波分解算子;‖（·）d‖1是细节小波系数的1-范数;σ≥0是正则化参数。

引入对数内点化函数，可将上述问题转化为

minx∈R^qr

12‖y-diag（S，…，S）x‖22+

σ∑qi=1‖（WPix）d‖1-

μ∑qi=1∑rj=1

lnxi，j+

∑rj=1

ln1-∑qi=1xi，j，（3）

郑 州 大 学 学 报 （理 学 版）第57卷 第2期董云达，等：求解高光谱解混的三算子分裂方法

其中：μ>0是障碍因子;

diag（S，…，S）表示块对角矩阵;

y∈R^sr、x∈R^qr分别表示矩阵Y、X拉直后的向量;

Pix=Xi、Pi∈R^r×n是抽取矩阵;σ=0.01。

本文中使用的是真实的高光谱数据集Urban数据集，s取162，q取6，r取256×256，小波分解算子选取的是超过2分辨率的正交db4小波分解矩阵。

此外，我们给出信噪比的定义

SNR=20lg（‖‖/‖x-‖），

其中：表示x的真实值。

2 算法

最近，文献［3］在无穷维实Hilbert空间中提出求解带有一个线性复合的三算子单调包含问题的自适应分裂算法，该算法是在文献［2］的基础之上，给出了邻近因子自适应选取准则。引入如下记号，

n=qr，Q=In

D，q=（0，…，0，-1，…，-1）T，

D=diag（a1，…，a1），a1=-（1，…，1）∈Rq，

H=diag（S，…，S）。

我们可以得到问题（3）的最优性条件为

0∈σ（‖（WPix）d‖1）+HT（Hx-y）+QTB（Qx-q），其中：

Bz=-μdiag［z^-11，…，z^-1p］。

文献［1］中PIPA在第l步的子问题为

minx∈R^qr

12‖y-diag（S，…，S）x‖22+

σ∑qi=1‖（WPix）d‖1-μl

∑qi=1∑rj=1

lnxi，j+∑rj=1

ln1-∑qi=1xi，j，

其中：μl>0是障碍因子。PIPA采用的是向前向后分裂方法，而在本文中，我们将每个子问题转化为如下三算子单调包含问题

0∈σ（‖（WPix）d‖1）+HT

（Rx-y）+QTB（Qx-q），

其中：Bz=-μldiag［z^-11，…，z^-1p］。我们参考文献［3］提出的自适应选取邻近因子的三算子分裂算法运用到求解上述子问题中可以表述为：

记m=65 536，选取初始点：x0=ones（6*m，1）/7，

y0=zeros（7*m，1），u0=zeros（7*m，1）， =0.45，α0=1，μ0=1，

θ=1.01。

计算

β=100×（‖Q‖1‖Q‖∞/4αk+1/4），

然后分别计算得到k、k、k，k=uk-（yk-Qxk+q）/β，（αkI+0.01‖（·）d‖1）（k）瘙綍αkxk-ak-QTk，ki-μl1ki=

yki+^ki，i=1，…，（q+1）r。

如果xk=k，uk=k则停止，否则计算

k=αk‖xk-k‖2+

‖yk-k‖2+

〈k-Qk+q，uk-k〉，

φk=‖xk-k‖2+‖yk-k‖2+

‖k-Qk+q‖2，

γk=kφk。

计算下一迭代点，

（αkI+RTH）（x^k+1）=

αkxk+ak-γk

（xk-k）+HTy，其中y是矩阵Y拉直后的向量（不要与迭代点yk混淆），

y^k+1=yk-γk

（yk-k），

u^k+1=uk-γk

（k-Qk+q），

a^k+1=αk（xk-x^k+1）+ak-γk（xk-k）。

最后更新邻近因子αk+1

αk+1=（1+τk）αk，若σk≤0.5，

（1-τk）αk，若σk≥2，

αk，其他，

其中：τk=0.1^k+1; σk选取为

σk=‖αk（x^k+1-xk）‖+

‖（y^k+1-yk）‖+‖u^k+1-uk‖‖HTH（x^k+1-xk）‖，

注：该调比技巧在文献［3］中给出，该调比准则是对文献［4］中处理两算子单调包含问题时提出的DR算法（相关的讨论参见文献［5］）相应部分准则的一个延伸。

根据文献［2］中的引理1.14、1.15、假设2.1和定理2.1，可以证明上述算法1的弱收敛性，详见文献［3］。

文献［1］针对该问题提出了一个邻近内点法，该算法的外迭代同样是使用内点法将问题转化为（3），内迭代则是采用向前、向后分裂算法。记f，φ为

f（x）=0.01∑qi=1‖（WPix）d‖1，

φμl（x）=12‖y-diag（S，…，S）x‖22-

μl∑qi=1∑rj=1

lnxi，j+∑rj=1

ln1-∑qi=1xi，j，

选择合适的变尺度矩阵Ak，通过计算

k（γ）=（I+γA^-1kf）^-1（xk-γA^-1k

Δ

φμl（xk））

得到候选点k（γ）。若γ=γk满足某个Armijo型步长准则，则下一迭代点

x^k+1=k（γk）。在实际操作中，变尺度矩阵Ak一般取I或是函数φμl在xk处的Hessian阵及其近似。其他相关参数选取详见文献［1］。

3 数值实验

本节运用算法1求解上述高光谱解混问题，并验证其有效性。本实验是由Matlab R2018b运行。

此外，我们还能将问题（3）转化为

0∈diag（S，…，S）T（diag（S，…，S）x-y）+

0.01‖（·）d‖1+QTδC（Qx-q），

其中：C=R^（q+1）r+;

δC表示集合C上的示性函数。这种情况下我们记作算法2。文献［1］中当变尺度矩阵

Ak恒为单位矩阵I时，我们记作算法3，当Ak取函数φμl在xk处的Hessian阵时，即

Ak=diag［STS，…，STS］+μldiag

1x211，…，1x2qr+

μl∑rt=1（eTxt-1）^-2eteTt，

记作算法4，其中：e=（1，…，1）T∈Rq，xt表示矩阵X的列向量，

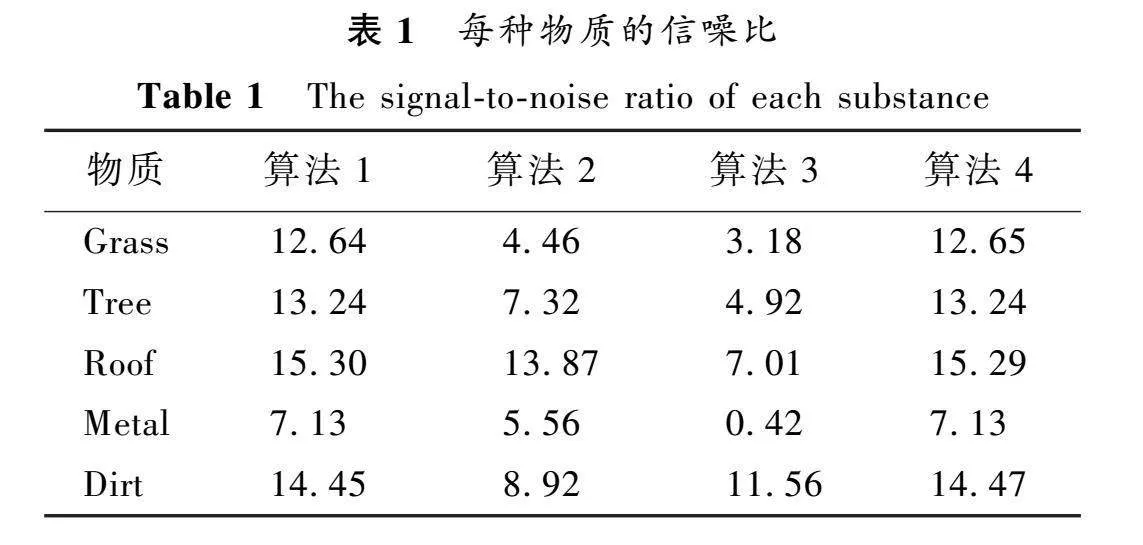
et∈R^qr表示从第（t-1）q+1行到第tq行元素为1，其余全为0的列向量。数值结果如表1。

表1展示的是四种算法分别用来处理高光谱解混问题获得的关于表中五种物质：草、树、屋顶、金属、泥土的信噪比，根据信噪比的定义我们可知，信噪比值越高说明算法的数值性能越好。通过观察表中数据，我们可以发现，算法1的数值效果远远超过算法3，并且与算法4的结果相差无几，这说明在不引入变尺度矩阵的情况下，我们的分裂算法效果更好。算法2的数值结果也优于算法3，但不如算法1和算法4，这说明对于求解该类问题来说，内点法要优于简单引入示性函数。

图1、图2分别展示了算法1、算法2、算法4关于屋顶、泥土这两种物质的丰度图和真实图像的对比图。通过对比不难发现，算法1和算法4效果优于算法2，并且二者效果差别不大。图3、图4分别 展示了相同迭代步数下精度和信噪比的比较，其中精度ε=lg（‖xk-x*‖/‖x*‖）。通过上图也能发现，算法1和算法4能达到更Dd5sqM58DBf/XQqPUgnoZg==高的精度和信噪比。

4 结论

本文将高光谱解混问题转化为求解三算子单调

包含。不同于引入示性函数，本文第二小节中的处理方式更容易发挥三算子分裂算法的性能，这是本文的主要贡献之一。综上所述，在不引入变尺度矩阵的情况下，算法1的数值效果远超算法3，并且能达到和引入变尺度矩阵Ak的算法4近乎相同的效果，但是运行时间相对久一些，因此后续我们可以考虑将变尺度矩阵Ak引入到我们的算法1之中，期待可以获得更好的数值结果。此外，参考文献［3］可知，算法1的应用范围更为广泛，参数选取更加简单实用。

参考文献：

［1］ CHOUZENOUX E， CORBINEAU M C， PESQUET J C. A proximal interior point algorithm with applications to image processing［J］.Journal of mathematical imaging and vision， 2020， 62（6/7）： 919-940.

［2］ DONG Y D. A new splitting method for systems of monotone inclusions in Hilbert spaces［J］. Mathematics and computers in simulation， 2023， 203： 518-537.

［3］ 张园园. 求解三算子单调包含的自适应分裂方法及其应用［D］. 郑州：郑州大学， 2023.

ZHANG Y Y. Adaptive splitting method for solving three-operator monotone inclusions with its applications［D］. Zhengzhou：Zhengzhou University， 2023.

［4］ DONG Y D， FISCHER A. A family of operator splitting methods revisited［J］. Nonlinear analysis： theory， methods & applications， 2010， 72（11）： 4307-4315.

［5］ 康倍倍， 董云达， 王亚丽. 关于凸极小化的Douglas-Rachford分裂方法的一个注［J］. 郑州大学学报（工学版）， 2017， 38（4）： 94-96.

KANG B B， DONG Y D， WANG Y L. A note on Douglas-rachford splitting method for convex minimization［J］. Journal of Zhengzhou university （engineering science）， 2017， 38（4）： 94-96.