架空地线临界融冰电流估算方法研究

基金项目：国网湖北超高压公司科技资助项目（B71520230043）

第一作者简介：王沐东（1996-），男，工程师。研究方向为变电运维技术。

*通信作者：文中（1968-），男，硕士，副教授。研究方向为输电线路试验理论与技术。

DOI：10.19981/j.CN23-1581/G3.2024.21.032

摘" 要：架空线路覆冰是影响电网正常运行较为严重的灾害之一，尤其地线更易出现覆冰，有必要对架空地线直流融冰电流进行计算，而现有的经验公式及应用较多的布尔斯道尔夫融冰电流计算公式较为复杂，且有些参数测量困难。因此，该文提出一种用于快速估算已知架空地线型号在不同风速、环境温度、覆冰厚度条件下临界融冰电流的方法，通过分析地线融冰物理过程，利用有限元软件搭建仿真模型，经模型计算得到数据集，然后采用多元线性回归拟合得到相关变量的函数表达式，并与计算值进行对比。

关键词：架空地线；直流融冰；融冰电流计算；有限元；多元回归

中图分类号：TM751" " " 文献标志码：A" " " " " 文章编号：2095-2945（2024）21-0136-04

Abstract： Overhead line ice is one of the more serious disasters affecting the normal operation of the power grid， especially the earth wire is more prone to ice， it is necessary to calculate the overhead earth wire DC melting current， and the existing empirical formulas as well as the application of the more Bursdorff melting current formula is more complex， and some of the parameters are difficult to measure. Therefore， this paper presents a method for quickly estimating the critical ice melting current of known overhead earth wire under the conditions of different wind speed， ambient temperature and icing thickness. The simulation model is built by finite element software， the data set is calculated， and then the function expression of related variables is obtained by multiple linear regression fitting， and compared with the calculated value.

Keywords： overhead earth-wire; DC ice melting; ice melting current calculation; finite element; multiple regression

架空线路覆冰曾对世界各地电网安全运行造成严重影响。美国、加拿大、日本等国都发生过严重冰雪事故，我国也出现不少冰闪跳闸和倒塔断线等事故[1]。目前国内外也提出了多种融冰计算模型，如融冰动态模型、融冰静态模型、椭圆融冰模型等[1-2]。文献[3-4]建立覆冰导线的物理数学模型对短路融冰过程中导线温度、冰层变化等动态参数进行仿真。但物理仿真模型的建立过程较复杂，不便于工程应用实施。而现有的融冰电流计算经验公式及应用较多的布尔斯道尔夫融冰电流计算公式中部分参数测量困难。因此，提出一种快速估算已知架空地线型号在不同风速、环境温度、覆冰厚度条件下临界融冰电流的方法。

1" 有限元仿真分析

1.1" 模型假设与简化

本文对架空地线直流临界融冰电流进行有限元仿真时采用以下定义与假设：①临界融冰电流定义为架空线路覆冰后，在风速、环境温度、覆冰厚度一定下能使冰层融化的最小电流[5]在模型中体现为冰层与导体相交面一点温度收敛于273.15 K时对应的电流大小。②架空线路覆冰形状主要受线路扭转刚度的影响，而地线直径小，扭转刚度较小，当迎风侧覆冰堆积后更容易发生扭转，以致其覆冰截面较接近圆形[6]，因此模型中简化为均匀覆冰。③由于对架空地线进行直流融冰时，通常有数十公里的融冰距离，这时地线轴向传热可忽略[7]。

1.2" 融冰物理过程分析

覆冰未发生相变前，融冰电流产生的焦耳热一部分用于加热冰层与导体，剩余部分通过热传导传递到冰层外表面经对流与辐射损耗在外界环境中，该过程中并不涉及相变焓，因此该阶段能量守恒方程可表示为

， （1）

式中：I为融冰电流，A；R为导线电阻，Ω；h为冰层外表面与外界环境传热系数，W/（m3·K）；Ti和Ta分别为冰层外表面温度、环境温度，K；ρθ为求解区域微元？兹物质密度，kg/m3；Cθ为求解区域微元？兹物质比热容，J/（kg·K）；dS为截面面积，m2；dT为Δt时间内温度变化量。

在冰层外表面有对流与辐射热交换，满足第三类边界条件，热流密度方程表示为

式中：λ为覆冰导热系数，W/（m·℃）。

对于架空地线融冰过程中的空气间隙，其尺寸较小，空气间隙内的热量传递依靠导热[8]。因此，在地线至冰层外表面之间的传热方式主要是热传导，满足热传导微分方程[9]

式中：T为温度分布函数；c为物质比热容，J/（kg·°C）；ρ为物质密度，kg/m3；qθ为求解区域内的内热源强度，W/m2。

1.3" 有限元仿真分析

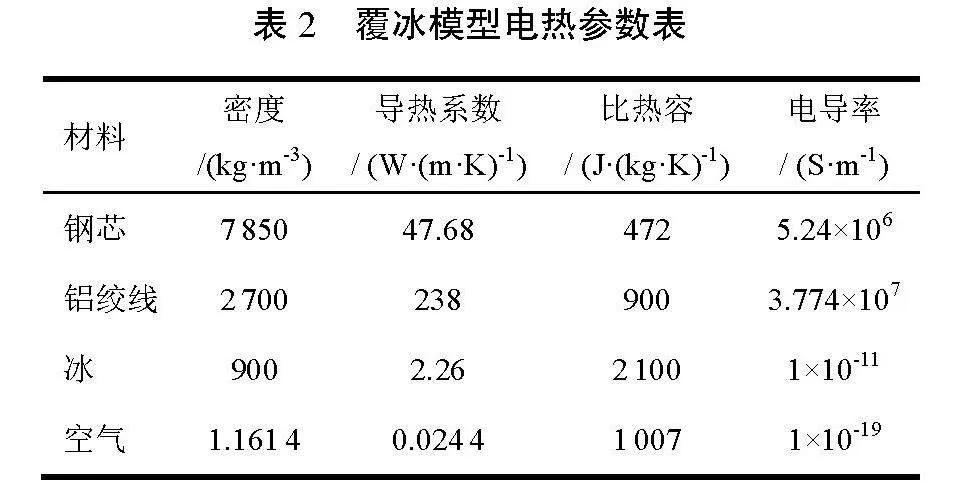
本文以LBGJ-120-40AC（JLB40-120）为例，型号参数见表1。架空线路覆冰类型选择对线路影响最大的雨凇，因此式中取λice=2.27×10-2，搭建电磁热-非等温流动耦合有限元仿真模型，对地线施加直流电流后进行温度场分析。覆冰模型电热参数见表2。

表2" 覆冰模型电热参数表

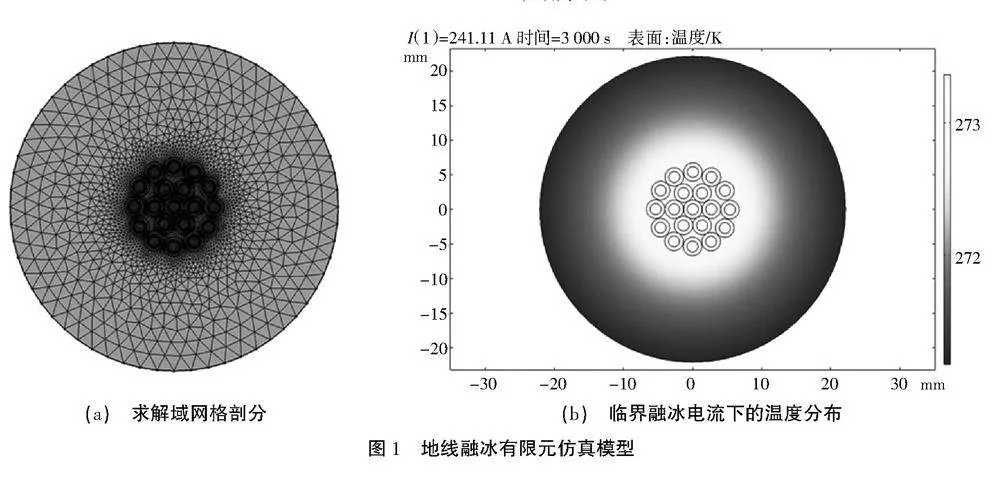
求解区域采用自由三角形网格剖分，由于模型目标为冰层与地线的交界面温度求解，选择在该界面进行局部网格细化提高计算精度，最终网格剖分如图1（a）所示。当设定风速为5 m/s，环境温度为268.15 K，覆冰厚度为15 mm时，通过模型计算得到临界融冰电流为241.11 A，此时冰层与地线温度分布如图1（b）所示。

2" 多元线性回归

有2个或者2个自变量以上的回归分析就称为多元回归，多元线性回归（MLR）一般用于得到不同自变量对因变量的影响程度，本文中自变量为风速、环境温度、覆冰厚度，因变量为相应的临界融冰电流。可建立多元线性回归模型为

， （4）

式中：因变量y为临界融冰电流；x1为风速序列；x2为环境温度序列；x3为覆冰厚度序列。常系数代表信息残留与全体信息关系。未知常量α0、α1、α2、α3称为回归模型系数，α0为常系数。常数项表示的是未被自变量解释的且长期存在（非随机）的部分，即信息残留。因变量y代表需要解释的全体信息，模型里的xi构成的空间是自变量解释空间，在自变量解释空间外，如果还有恒定的信息残留，那么这部分信息构成常数项。随后引入概率密度函数将回归关系问题转变为概率问题[10]

此时就把求解回归系数αi的过程转为解出全部概率密度函数的最大乘积结果的过程

通过以上的算法公式便可以求得多元回归方程的回归系数，从而判断相关影响因素对架空地线直流临界融冰电流的影响大小。将其变形为矩阵形式可得

，（8）

将其展开后求导为0，可得

求得解析解为

。" " "（10）

而对于多元回归分析的精准度判断则是用拟合优度R2，首先要计算残差平方和Q=∑（y-y*）2和∑y2，其中y为有限元仿真模型计算值，y*为多元线性回归返回值，然后拟合优度R2=1-（Q/∑y2）0.5，其值越接近1，拟合效果越好。

利用搭建的有限元仿真模型计算得到的风速为1～5 m/s，环境温度为263.15～272.15 K，覆冰厚度为5～25 mm的数据集进行多元线性回归拟合，最终得到多元回归模型拟合优度R2为0.970 2，其回归系数为

？兹＝[？琢0，？琢1，？琢2，？琢3]

=[6 249.392，11.071 859 72，-22.728 3，1.443 724]。（11）

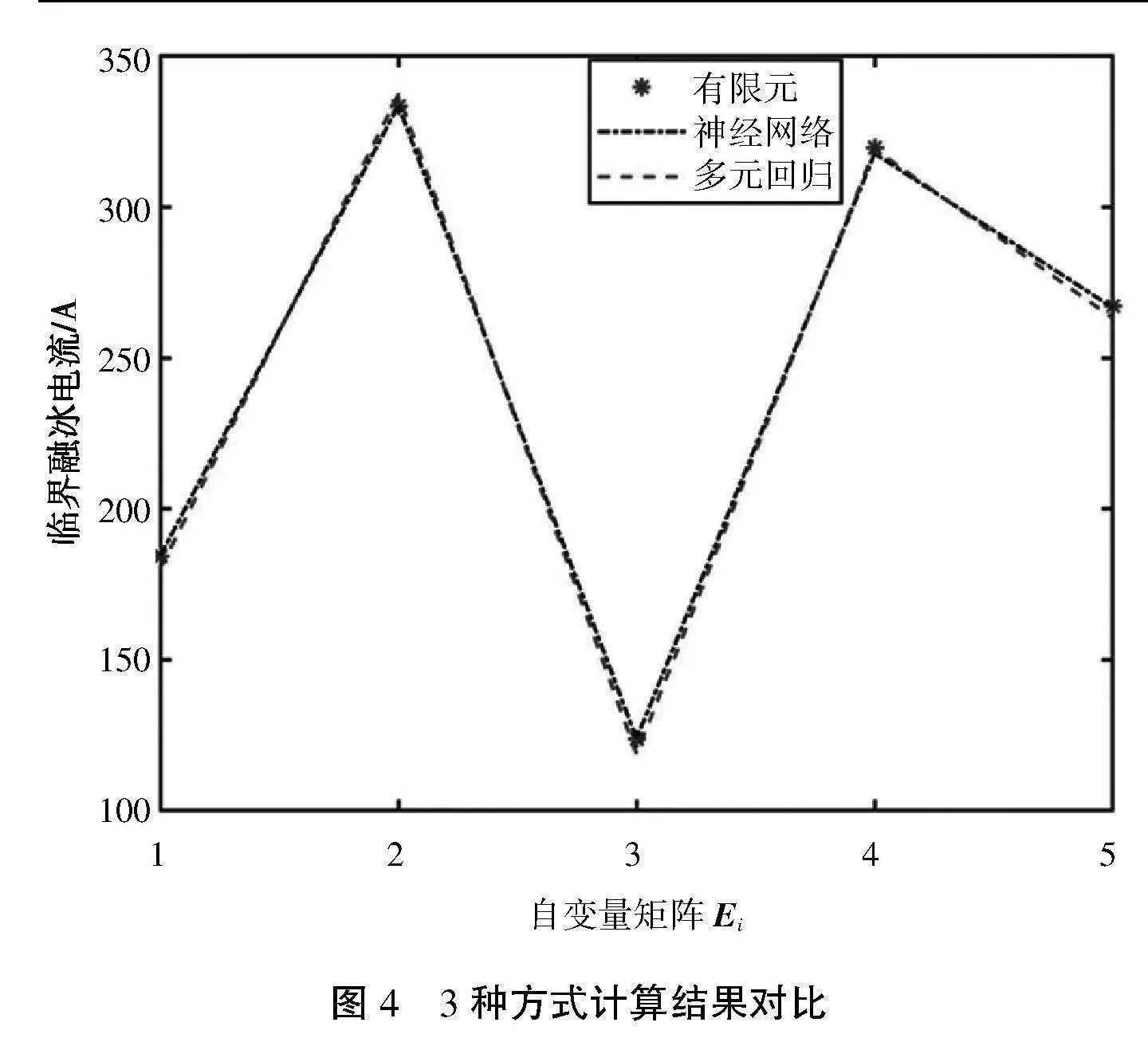
然后通过此拟合公式估算随机5个自变量矩阵Ei=[风速 温度 厚度]对应的临界融冰电流见表3，并与有限元仿真计算模型与神经网络预测值进行对比，如图2所示。

从表3、图2可看出所得拟合表达式与实际值较为吻合，虽然拟合程度弱于神经网络，但由于其形式简洁仅为三元一次函数表达式，在架空地线融冰工程中，能够方便工作人员快速估算地线在对应条件下的临界融冰电流。

图4" 3种方式计算结果对比

3" 结束语

本文提出了一种架空地线临界融冰电流估算方法，通过分析直流融冰物理过程搭建出电磁热-非等温流动耦合有限元仿真模型，然后将计算得到的数据集进行多元线性回归拟合出估算表达式。结果表明拟合优度为0.970 2，最后和有限元仿真计算模型及神经网络拟合值做了对比，虽然效果逊于神经网络，但通过多元线性回归拟合的表达式，能够方便工作人员快速估算地线临界融冰电流。

参考文献：

[1] 赵杰，饶宏，李立浧．电网防冰融冰技术及应用[M]．北京：中国电力出版社，2010．

[2] 蒋兴良，易辉．输电线路覆冰及防护[M]．北京：中国电力出版社，2002．

[3] P？魪TER Z. Modeling and simulation of the ice melting process on a current-carrying conductor [D].Québec： Université Du Québec，2006．

[4] HORW I C，DAVIDSON C C，GRANGER M. An application of HVDC to the de-icing of transmission lines[C]//2005/2006 IEEE/ Pes Transmission ＆ Distribution Conference ＆ Exposition，2006．

[5] 张益修，李健，赵全江，等.长距离地线融冰及工程实践[J].电力勘测设计，2015（2）：51-55.

[6] 李铁鼎，李健，吕健双，等.输电线路地线融冰的热平衡分析与计算[J].电力建设，2015，36（4）：70-76.

[7] HE Z， ZHAO B H， HONG C X， et al. DC ice-melting operation of the ground wire based on the characteristic investigation of the thermal structure coupling effect[J]. Electric Power Systems Research，2023，218（1）：1-9.

[8] 杨世铭，陶文铨.传热学[M].4版.北京：高等教育出版社，2006.

[9] 孟志高.光纤复合架空地线（OPGW）直流融冰过程与模型研究[D].重庆：重庆大学，2017.

[10] 马旭.基于深度置信网络和多元线性回归的风电功率预测研究[D].太原：太原科技大学，2021.