巧用配速法解复合场问题

［摘 要］当带电粒子在复合场中的运动既不是匀速圆周运动，也不是匀速直线运动时，情况变得复杂，此时运用配速法能有效解决问题。配速法基于运动的合成与分解原理，通过配速，将带电粒子在复合场中的曲线运动分解为匀速直线运动和匀速圆周运动两个分运动。配速法一分为二、化繁为简，有助于学生顺利解决问题。

［关键词］配速法；复合场；匀速直线运动；匀速圆周运动

［中图分类号］ " "G633.7 " " " " " " " "［文献标识码］ " "A " " " " " " " "［文章编号］ " "1674-6058（2024）29-0050-04

高中物理中，带电粒子在复合场中的运动问题是核心知识点，同时既是教学重点，又是高考热点。这类问题具有综合性、系统性和多样性的特点，其解答常需融合力学、电磁学及数学知识，能够全面考查学生的综合能力。关于带电粒子在复合场中因合外力为零而做匀速直线运动，以及电场力与重力平衡、洛伦兹力提供向心力而做匀速圆周运动的情况，本文不再赘述。

若带电粒子在磁场中除受洛伦兹力外，还受其他力，且其合力不为零，则带电粒子的速度大小和方向会改变，进而导致洛伦兹力和合外力也随之变化，在这种情况下，带电粒子将做复杂的曲线运动。为了分析和解决这一问题，本文采用速配法进行思维引导和求解。

一、配速法的基本原理

配速法的基本原理是运动的合成与分解。在处理带电粒子在复合场中的运动问题时，其核心思想是将一个复杂的运动分解为两个或多个较为简单的分运动。具体分解方法如下：

（1）若带电粒子的初速度为零，则将速度分解为两个等大、反向的分速度（相当于配设一对等大、反向的速度），使一个分速度对应的洛伦兹力与复合场中的恒力平衡，带电粒子做匀速直线运动；而另一个分速度对应的洛伦兹力提供向心力，使带电粒子做匀速圆周运动，如图1所示，其中[v0=0，v1=v2]。

（2）若带电粒子的初速度不为零，同样配上一对等大、反向的速度[v1]和[v2]，如图2所示。根据运动的合成与分解，带电粒子的速度仍然是[v0]，使其中一个速度（[v1]）所对应的洛伦兹力与复合场中的恒力（重力或电场力或重力和电场力的合力）平衡，带电粒子做匀速直线运动；另一个速度（[v2]）与初速度[v0]的合速度（[v]）所对应的洛伦兹力提供向心力，带电粒子做匀速圆周运动。通过配速，除已经平衡恒力的洛伦兹力所对应的速度外，另一个分速度与初速度共线，若二者速度方向相同，则做匀速圆周运动的速度为两者之和，反之为两者之差，如图3所示。

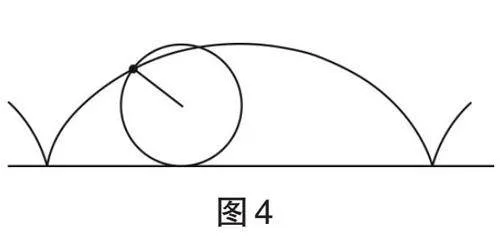
带电粒子在复合场中做复杂的曲线运动，运动轨迹既不是直线也不是圆，而是类似向前匀速行驶的自行车轮胎边缘上的一个点的运动，运动轨迹是一条摆线（一个圆沿一条直线运动时，圆边界上一定点所形成的轨迹），如图4所示。通过合理配速，将带电粒子在复合场中复杂的曲线运动转化为两个简单、常规且容易处理的匀速直线运动和匀速圆周运动，方法简便，思路清晰，既降低了问题的难度，又提升了解题的效率。

二、题型分析

根据复合场的存在形式与带电粒子初速度的不同，可以分为以下四种常见题型。

（一）初速度为零，磁场与重力场（或电场）型

物理情境：带电粒子的初速度[v0=0]，复合场为正交的磁场与重力场（或电场），如图5所示。

思维方法：把初速度[v0]分解为一个向右的速度[v1]和一个向左的速度[v2]，且[v1=v2]，如图6所示，使与[v1]对应的洛伦兹力[F]洛1和重力G（或电场力）平衡，带电粒子做匀速直线运动；而与[v]2对应的洛伦兹力[F]洛2提供向心力，带电粒子做匀速圆周运动。

（二）初速度为零，磁场、电场与重力场型

物理情境：带电粒子的初速度[v0=0]，复合场为正交的磁场、电场和重力场，如图7所示。

思维方法：把初速度[v0]分解为一个向右的速度[v1]和一个向左的速度[v2]，且[v1=v2]，如图8所示，使与[v1]对应的洛伦兹力[F]洛1和[F]（重力和电场力的合力）平衡，带电粒子做匀速直线运动；而与[v2]对应的洛伦兹力[F]洛2提供向心力，带电粒子做匀速圆周运动。

（三）初速度不为零，磁场与重力场（或电场）型

物理情境：带电粒子的初速度[v0≠0]，复合场为正交的磁场与重力场（或电场），如图9所示。

思维方法：配设一对等大、反向的速度[v1]和[v2]，如图10所示，使与[v1]对应的洛伦兹力[F洛1]和重力G（或电场力）平衡，带电粒子做匀速直线运动；而与[v0]和[v2]的合速度[v]（若[v0]和[v2]在同一直线上，则同向相加，反向相减；若[v0]和[v2]不在同一直线上，则用平行四边形定则求解）对应的洛伦兹力[F]洛2提供向心力，带电粒子做匀速圆周运动。

（四）初速度不为零，磁场、电场、重力场型

物理情境：带电粒子的初速度[v0≠0]，复合场为正交的磁场、电场和重力场，如图11所示。

思维方法：配设一对等大、反向的速度[v1]和[v2]，如图12所示，使与[v1]对应的洛伦兹力[F]洛1与重力和电场力的合力[F]平衡，带电粒子做匀速直线运动；而与[v0]和[v2]的合速度[v]（若[v0]和[v2]在同一直线上，则同向相加，反向相减；若[v0]和[v2]不在同一直线上，则用平行四边形定则求解）对应的洛伦兹力[F]洛2提供向心力，带电粒子做匀速圆周运动。

三、应用举例

［例1］如图13所示，平面直角坐标系[xOy]位于竖直平面内，[x]轴方向水平向右，[y]轴竖直向上，坐标系[xOy]所在的空间有一正交的匀强电磁场，匀强电场方向竖直向下，场强大小为[E]；匀强磁场方向垂直纸面向里，磁感应强度大小为[B]。一个电荷量为[q]、质量为[m]的带正电的小球（可视为质点），以大小不同的初速度从坐标原点[O]沿[x]轴正方向对准[x]轴上的[A]点射出。不计空气阻力，重力加速度为[g]。（1）若小球做直线运动通过[A]点，求此时小球的初速度大小[v0]。（2）若小球的初速度大小[v′0≠v0]，射出小球后，小球会经曲线运动通过[A]点，求[A]点的坐标值[xA]。（3）若小球从[O]点由静止释放，求小球运动过程中可达到的最大速率[vm]和小球到[x]轴的最大距离[H]。

解析：（1）因小球沿直线运动通过[A]点，根据平衡条件有[qv0B=qE+mg]，解得[v0=qE+mgqB]。

（2）若小球的初速度大小[v′0≠v0]，则小球在竖直平面内做曲线运动，给小球配设一对等大、反向的速度[v1]和[v2]，如图14所示，[v1]水平向右，所对应的洛伦兹力与电场力和重力的合力平衡，小球沿[x]轴向右做匀速直线运动。

根据平衡条件[qv1B=qE+mg]，得[v1=qE+mgqB]。

水平向左的分速度[v2]与初速度[v0]的合速度[v=v2-v0]，所对应的洛伦兹力提供向心力，小球做匀速圆周运动。

若[v=v2-v0gt;0]，则其方向向左，对应[x]轴下方的逆时针方向的匀速圆周运动；

若[v=v2-v0lt;0]，则其方向向右，对应[x]轴上方的逆时针方向的匀速圆周运动。

则根据[qvB=mv2r]和[T=2πrv]得匀速圆周运动的周期[T=2πmqB]。

要使小球通过[A]点，则有[t=nT]（n=1，2，3…）。

小球沿[x]轴正向做匀速直线运动，则有[xA=v1t]，解得[xA=2nπm（qE+mg）q2B2]（n=1，2，3…）。

（3）小球从[O]点由静止释放后的运动可视为沿[x]轴正方向速度为[v0]和沿[x]轴负方向速度大小为[v0]的合运动，前者对应的洛伦兹力与电场力和重力的合力平衡，根据平衡条件[qv0B=qE+mg]，得[v0=qE+mgqB]。

后者对应的洛伦兹力提供向心力，在[x]轴下方做逆时针方向的匀速圆周运动，根据牛顿第二定律[qv0B=mv20r]，得[r=m（qE+mg）q2B2]。

经半个周期，小球在最低点两个分速度相同，对应的合速度最大，最大运动速率[vm=2v0=2m（qE+mg）qB]。

小球到[x]轴的最大距离为圆的直径，即[H=2r=2m（qE+mg）q2B2]。

点评：本题第（1）问比较基础，第（2）（3）问有一定的难度，需要利用第（1）问的平衡知识和配速法，将复杂的曲线运动分解为匀速直线运动和匀速圆周运动的合运动来处理。通过练习，体现了用配速法解决带电粒子在复合场中的复杂曲线运动问题的一般思维方法。

［例2］如图15所示，第一象限内存在水平向左的匀强电场，电场强度大小为[E]（[E]未知），第二象限内存在垂直纸面向里的匀强磁场，第三象限内存在垂直纸面向外的匀强磁场及竖直向下的匀强电场，电场强度大小为[2E]。现有一电荷量为[q]、质量为[m]的带正电粒子从[x]轴上的[A]点以初速度[v0]垂直[x]轴射入电场，经[y]轴上的[P]点进入第二象限。已知第二、三象限内磁感应强度的大小均为[B=Ev0]，[A]点的横坐标为[L 2]，[P]点的纵坐标为[L]，不计粒子重力。求：（1）电场强度[E]的大小；（2）粒子进入第二象限的磁场区域后，第一次经过[x]轴的位置到坐标原点的距离；（3）粒子第一次在第三象限运动过程中与[x]轴的最远距离。

解析：（1）粒子在第一象限电场中做类平抛运动，如图16所示。竖直方向有[L=v0t]，水平方向有[L2=vx2t]，解得[vx=v0]，又[vx=qEmt]，解得[E=mv20qL]。

（2）设粒子离开电场时，速度大小为[v]，方向与[y]轴正方向的夹角为[θ]，则速度大小[v=v20+v2x]，解得[v=2v0]。由几何关系得[tanθ=vxv0]，解得[θ=45°]。

设粒子在第二象限磁场中做匀速圆周运动的半径为[r1]，由牛顿第二定律得[qvB=mv2r1]，解得[r1=2L]，则粒子在第二象限运动轨迹圆心恰好落在[x]轴上。粒子第一次与[x]轴相交时到坐标原点的距离[d1=r1+r1cos45°]，解得[d1=（2+1）L]。

（3）由图16可知，粒子进入第三象限时的速度大小为[v3=v=2v0]，方向竖直向下，可在水平方向上配设水平向左的速度[v1]和水平向右的速度[v2]，使[v1]所对应的洛伦磁力与电场力平衡，满足[qv1B=2qE]，由题可知[B=Ev0]，解得[v1=v2=2v0]，[v3]与[v2]的合速度大小为[v4=v23+v22=2v0]，[v4]与[x]轴方向的夹角为[α=45°]。

所以粒子进入第三象限后在以[v4]对应的洛伦兹力提供向心力做匀速圆周运动的同时，以[v1]向左做匀速直线运动。

设粒子在第三象限做匀速圆周运动的半径为[r2]，由牛顿第二定律有[qv4B=mv24r2]，解得[r2=2L]。由几何关系得[d2=r2+r2cos45°]，解得[d2=（2+2）L]。

点评：本题物理过程复杂，对考生能力要求较高。从物理情境来看，包含三个主要过程：一是带电粒子在纯电场中的类平抛运动；二是带电粒子在纯磁场中的匀速圆周运动；三是带电粒子在复合场中的一般运动。针对每个过程，需应用相应的物理规律列出方程，并结合题设条件及运动轨迹求解。其中，第（3）问带电粒子在复合场中的运动较为复杂，可通过运动的合成与分解，运用配速法进行分析和解答。

经过对问题进行深入讨论与分析发现，利用配速法解决带电粒子在复合场中的一般曲线运动问题，可概括为两步：一是进行配速，依据运动的合成与分解原理，为带电粒子配设一对等大、反向的速度；二是进行分解，通过合理分配速度，将带电粒子的复杂运动分解为匀速直线运动与匀速圆周运动两个分运动来分别处理。此方法能条理化综合问题，简单化复杂问题，实现既快捷明了又科学高效地解答问题。

（责任编辑 " "黄春香）