体现课程内容结构化的教学思考

“比”在小学数学课程中是核心概念，很多概念与它都有关联，比如“比差”“比倍”“比快慢”“分数”“比”，这些概念的核心聚焦“关系”，基于“比较”实现认知路径的贯通性，具体包括“识别比较对象、确定比较标准、寻找两者间的关系、表达关系、应用关系”等过程，学习进阶体现为不同关系的认识以及比较过程中具体环节的各有侧重。对“比”及其相关内容进行分析，可以体现“学习内容整体性”“学科本质一致性”“学习过程阶段性”的特征，体现课程内容结构化，有助于发展学生的核心素养。下面对“比”及其相关内容的本质、认知路径以及教学进阶进行具体阐述。

一、基于“关系”的贯通思考

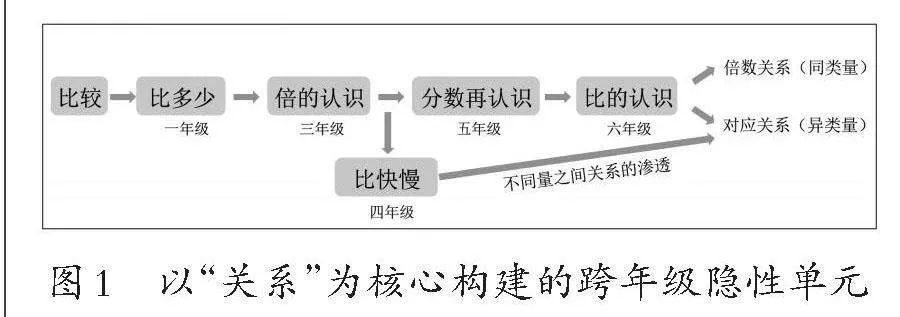
“比”及其相关内容在小学数学“数与代数”领域中，主要涵盖了五个核心内容：一年级的“比多少”、三年级的“倍的认识”、四年级的“比快慢”、五年级的“分数再认识”、六年级的“比的认识”（如图1）。这种跨年级课程内容的重新整合，是基于它们共同的数学本质——关系。通过这种贯通思考，能够帮助学生更全面、更系统地理解“比”及其相关概念，形成更深刻、更连贯的认识。

1.“比”及其相关内容的数学本质。

“比”及其相关内容的数学本质是关系。关系，作为一种特定的互动与联结方式，揭示了两个或更多事物、对象及其特性间相互作用、相互影响、相互依赖和相互比较的一种形式[1]。这种关系具有内在的相对性质。

在哲学史上，古希腊的哲学家亚里士多德最早提出“关系”范畴，他所说的关系是“有些东西由于它是别的东西的，或者以任何方式与别的东西有关，因此不能离开这别的东西而加以说明”。以师生关系为例，这种关系的形成必然涉及教师和学生两个主体。只有当这两个主体同时存在并相互作用时，我们才能称之为师生关系。在此过程中，单独的一方并不足以构成这种关系。所以，当我们谈论“关系”时，必然涉及至少两个“关系项”的相互作用。在数学的语境下，这种关系可以表述为aRb的形式，其中R代表关系，a和b则代表这种关系所涉及的两个关系项[2]。那么，关系的本质反映到“比”及其相关的内容中，是如何体现的呢？

2.“比”及其相关内容的具体分析。

“比多少”的数学本质是运用减法算式表达两个量之间的比较，涉及局部与整体之间的关系、不同对象比较的关系以及运动与变化中的关系[3]。两个对象间的数量比较，产生“多几”或“少几”的问题。对低年级的学生来说，减法计算不是问题，难在理解比较的关系上。这是减法意义的拓展，需要从局部与整体之间的关系过渡到比较关系。因此，认识核心应放在比较关系上。

“倍”的数学本质是运用倍数关系表达两个量之间的比较。倍数关系能表示不同对象之间的关系，也能表示一个量变化前后的关系。在英文表达里，“times”一词常用来体现倍数概念，比如“2×3”被表达为“2times3”，其中，“times”表明了次数的概念，表示“3出现了2次”。所以，当选定单位量后，这个单位量重复出现的次数代表了倍数，可以说，单位量是产生倍数的原因。因此，“倍的认识”的核心是认识比较关系中的单位量。

“比快慢”中的快慢，数学术语就是速度。速度在小学数学教材中的定义是“每小时（或每分、每秒等）行的路程”，实际上它反映的是运动物体时间、空间这两个不可分割的属性之间的关系[4]，具体体现为路程与时间之间的成正比关系。英国哲学家罗素（Russell）认为，速度是强度量，不具备直接度量的属性，与长度、面积等可直接度量的量有所不同，不具有可加性[5]。与之相对应的是广延量，这类量如长度、面积、体积等可以直接度量。汤普森（Thompson）进一步阐释了广延量的度量方式，他提出广延量可以通过与之同类的标准单位来度量。而强度量的单位则源自人心智的构造，例如速度，即路程与时间的比率（rate），便是人类根据自身对运动物体的观察和理解所创造出来的[6]。因此，“比快慢”的核心是两类广延量之间的关系。

“分数”有两层意义：量和率。前者表示数量多少，后者表示数量之间的倍数关系。表示倍数关系的分数在教材中的进阶体现为：三年级学的单位“1”是一个具体物体时，部分与整体之间的比率关系（真分数）；五年级学的单位“1”是由多个物体组成的整体时，部分与整体之间的比率关系（真分数）；五年级接着学两个数量之间的倍数关系（真分数、假分数），属于部分与部分之间关系的问题解决。例如，鸡2只，鸭5只，鸭是鸡的几分之几？但是现有的教材在部分与部分之间的关系认识方面有缺失。因此，“分数再认识”的核心是单位“1”是由多个物体组成的整体时，部分与部分之间的关系。

“比”是运用除法表达两个量之间的比较。比具有“运算说”和“关系说”的双重含义。“比”首先不是运算，而是对事物之间量的比较过程，在比较过程中发现关系，而后对关系进行表达，运算是这一过程中可能使用的工具和方法[7]。可见，“比”的本源应该是“比较”。此外，“比”可以分为同类量之比和不同类量之比，但同类量之比是“源”，不同类量之比是“流”。因此，“比”的认识核心是关系，在此基础上还要区分“源”和“流”，分清主次。

二、贯穿“比较”的认知路径

认识关系，离不开比较。比较是指确定对象之间差异点和共同点的逻辑方法，是人类认识世界，研究和理解事物的一种基本思维方法。人们根据一定的需要和标准，把彼此有某种联系的事物加以分析、对比，从而找出它们的内在联系、共同规律和特殊本质[8]。理解比较需遵循三个关键步骤：选择比较对象、确定比较特征、解释异同。在数学中，比较关系的认知过程包括：识别对象、确定标准、寻找关系、表达关系以及应用关系。

1.识别对象。

比较对象的识别，体现为对量的识别，涉及前文谈到的广延量和强度量，由此分析“比多少”“倍”“比快慢”“分数再认识”“比”这五个内容中的比较对象。

“比多少”中，比较的对象是两个广延量。比如，妹妹有3个苹果，哥哥有6个苹果，比较的广延量是“妹妹的苹果个数”和“哥哥的苹果个数”；“倍”“分数再认识”“比”的比较对象也都是两个数量不等的广延量；“比快慢”的对象是速度，其实是路程和时间之间的关系，指的是强度量，强度量本身就是路程和时间之间的关系，因此“比快慢”的比较对象是关系。需要说明的是，“比”的对象可以是两种量，也可以是多种量。

2.确定标准。

比较离不开标准。人们为了规范、统一地计数、度量、比较一类或几类对象，都需要约定统一的标准单位，如计数单位、长度单位等，这些单位具有客观、统一、确定的特点。此外，还有主观、个性和多样的“意念单位”，是对标准单位的复合和抽象创造。比如，小明有4个梨，小花有8个梨，小花的梨的数量就是小明的2倍，就是把“4个”作为单位。对“倍”和“比”的学习要从标准单位走向意念单位，这就需要学生看单位的眼光产生改变，实现从“一”到“多”的转变。由此分析“比多少”“倍”“比快慢”“分数再认识”“比”这五个内容中“标准”的确定。

“比多少”，两个广延量都可以作为标准，比“多几”时，是以“少的量”为标准；比“少几”时，是以“多的量”为标准，都表示两个量之间绝对的相差关系。“倍”是两个量之间相对的关系，是以两个量中数量少的量为标准。“分数再认识”与“倍”的标准刚好相反，是以数量多的量为标准。比如，6个苹果是2个苹果的3倍，是以2个苹果作为标准；2个苹果是6个苹果的[13]，就是以6个苹果作为标准。“比快慢”，实际上比的是关系的关系，标准既可以是强度量①，也可以是强度量②。“比”的标准是第三种量，如，4厘米和6厘米的比是2∶3，就是因为用“意念单位”2厘米分别去量4厘米和6厘米，得到2份和3份的关系。

3.寻找关系。

寻找关系，就是比较的对象异中求同以及同中求异的过程。异中求同，两个不同的比较对象，当把其中一个对象看作标准时，就能找到另一个对象与标准相同的地方，比如，6个苹果和2个苹果比较，以2个苹果为标准，6个苹果里有跟标准2个苹果一样的个数。有了异中求同，就能够有同中求异，和标准不一样的地方显而易见，可以是多了4个苹果的相差关系，也可以是6个苹果是2个苹果的3倍这样的份数关系。当以6个苹果为标准时，又找到了2个苹果是6个苹果的[13]。由此进入“比多少”“倍”“比快慢”“分数再认识”“比”这五个内容中寻找关系。

“比多少”是相差关系，比的是个数。“倍”“分数再认识”“比”是份数关系，比的都是份数，这个份数跟选定的标准有关系。“比快慢”实际上就是比速度，速度本身是关系，因为比速度就是在比关系的大小，其前提是要认识到速度本身是路程和时间之间的关系。

4.表达关系。

找到了关系，就要对关系进行表达。“比多少”是用减法得到两个量之间的差，“倍”“分数再认识”“比”都是用除法得到两个量之间的倍数，“比快慢”先是用除法得到速度，再用减法得到两个速度的相差关系。

5.应用关系。

在经历“识别对象、确定标准、寻找关系、表达关系”之后，对一个概念的初步理解就基本完成了。此刻，还需要在新的情境中进行应用。美国教育心理学家布鲁姆（Bloom）把认知思维目标分为六个层次：记忆—理解—应用—分析—评价—创新[9]。其中，应用关系就是对所学的概念、法则、原理的运用，体现了把学到的知识应用于新的情境和解决实际问题的能力。应用是以记忆和理解为基础的，是较高水平的理解，属于高阶思维。

以上阐释的五条，不仅是一个比较的过程，更是学生认识关系的重要路径。这一路径与亚历山大在《活跃的思维》一书中提出的智力五层次理论紧密相关[10]，同时与数学核心素养的培养目标相契合（如图2）。数学教育的核心目标之一是促进学生的心智发展。在这一过程中，智力五层次模型发挥至关重要的作用。该模型由内至外分为多个层级。其中，最内圈是心智模型，它是理论基础，涵盖了感知、推理、想象、语言和文化五个方面。每个层级都与中间“比较”的认知过程相呼应，即识别对象、确定标准、寻找关系、表达关系和应用关系。这一认知过程也与数学教育的“三会”目标在一定程度上相对应。这一模型不仅有助于培养学生的核心素养，还能够揭示认知过程的内在规律，为开发核心内容的学习进阶和教学设计提供帮助。

三、构建“进阶”的学习过程

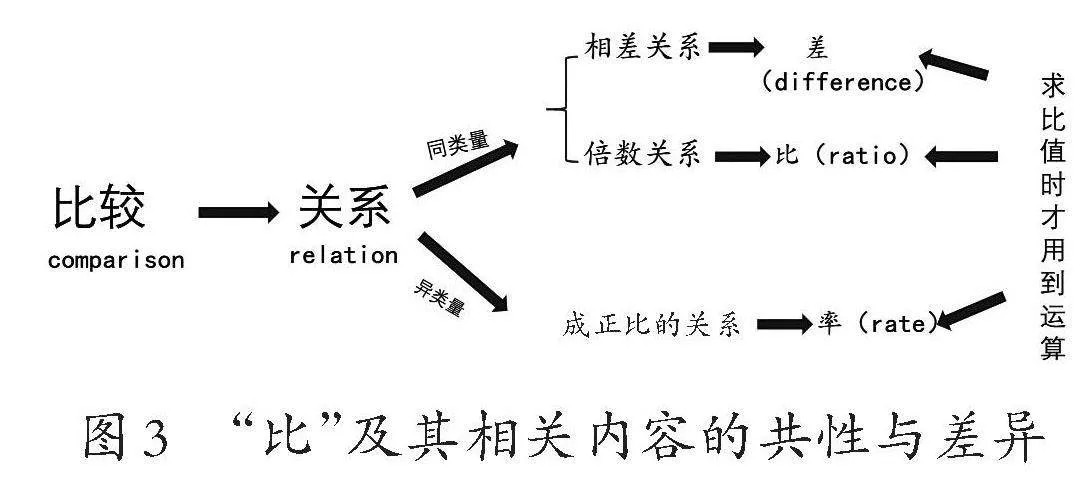
学习内容的差异性决定学习过程的阶段性。从关系的角度来看，“比”的意义有三层不同的含义：相差关系、倍数关系以及成正比关系（如图3）。认识这些关系，都离不开比较。在数学的比较里有两类：一类是比较多少，属于相差关系的比较，得到差；另一类是比较份数，属于倍比关系的比较，小学数学课程中的倍、分数、比都是这种比较，不同之处在于关系表达的形式不同，但是其本质都是两个量之间的倍数关系，而比快慢涉及不同类量的比。

这三种不同关系的认识，放在比较的认知框架下，能发现知识内容的差异，也就能知道各个内容的学习进阶。“学习进阶”是“搭建起一座连接对学习的研究和课堂教学实践的桥梁”[11]。其内涵是在一个较大时间跨度内，学生对某一学习主题的思考和认识不断丰富、精致和深入的过程，旨在揭示学生对该主题的思考、理解与实践活动在相当长的一段时间内是如何从简单到复杂、从低水平到高水平、从新手到专家逐步发展的[12]。表1以比较的认知框架分析了“比”及其相关内容的异同，力图实现学生对数学学科本质的理解，形成知识与方法的迁移，实现核心素养的阶段性发展。

从表1可以看出，在“比多少”的学习中，形成比较的思维，重点解决“确定比较的标准”，突出既可以以“多的量”为标准，又可以以“少的量”为标准。为了凸显比较关系的认识，“谁比谁少几”的问题和“谁比谁多几”的问题要同等重视。

“倍的认识”中，重点解决发现“份”的关系，比较的过程落在“确定比较的标准”与“寻找关系”这两步。相比于相差关系，倍的认识的比较标准有两个变化：一是从比较的对象互为标准变成了以少的量为标准；二是从比个数变成了比份数，从数量比变成了份数比。在这里，“确定比较的标准”是重点，“实施比较”得到份数比是难点。

“分数再认识”，目前在教材中更多的是表示部分与整体之间的关系，表示部分与部分之间的关系是目前教学中需要加强的部分，旨在突出量与量之间的比较。在分数的初步认识中，学生已经积累了用一个分数可以表达部分和整体之间的关系。在这个经验的基础上，分数的再认识需要认识分数可以表达两个量之间的倍比关系，既然是两个量之间的倍比，那么两个量可以互为标准。因此，“分数再认识”的进阶体现在解决“确定比较的标准”上。

“比快慢”，同类量的比是源头，不同类量的比是发展。在学习比之前，速度的认识渗透了不同类量之间的比。重点在“识别比较的对象”，因为比速度的快慢并不是由一个因素决定的，而是需要两个因素共同决定，这个识别的过程需要学生自己寻找，从而积累自主寻找比较对象的经验。

“比的认识”，有了以上比较关系的经验积累，有了份的关系的认识，重点解决用两个量之间份的关系（倍比关系）解决问题，突出表达的原始性，实现自由应用。因此，“比的认识”的进阶体现在“倍数关系的表达”，通过“什么样的表达更能灵活地解决问题”，达成应用比较的路径实现迁移式学习。

四、体现整体把握的教学建议

从“比较”的视角看，“比多少”“倍的认识”“比快慢”“分数再认识”“比的认识”这五个内容，在已有的教学中存在的问题主要是突出关系本质不够，比较中实现关联不足（见表2）。

从表2可以看出，以上核心内容基于“比较”的关联略显不足。威金斯和麦克泰格曾讲过，单课时间太短，不能实现复杂的学习目标。当然，单课计划理应依从单元计划：当一节课被包含在更大的单元和课程设计中时，通常会更有目的性和连接性。因此，以上内容可以统整为跨年级的大单元，改进方向是“比较贯穿，突出关系”。

具体体现为：第一，聚焦关系，突出本质，即学科本质突出关系，在比较的过程中实现教学的整体性；第二，比较贯穿，实现关联，经历“识别比较的对象、确定比较的标准、寻找关系、表达关系、应用关系”的认知过程，形成认识关系的结构化思维；第三，在比较的过程中，不断深化对数量之间关系的理解，螺旋进阶，发展素养。

参考文献：

[1][8]《哲学大辞典》编辑委员会.哲学大辞典[M].上海：上海辞书出版社，1992：661，184．

[2]ERTRANDRUSSELLMA.Theprin-ciplesofmathematics[M].Cambridge：Cambridgeuniversitypress：85．

[3]郜舒竹.算式与情境的辩证关系[J].教学月刊·小学版（数学），2017（4）：12-15．

[4]汤牧文，郜舒竹．“速度”之难与教学改进[J].教学月刊·小学版（数学），2021（11）：4-10．

[5]RUSSELLB.Ontherelationsofnumberandquantity[J].Mind，1897（6）：326-341．

[6]THOMPSONPW.Quantitativeconceptsasafoundationforalgebra[J].Annualmeetingofthenorthamericanchapteroftheinternationalgroupforthepsychologyofmathematicseduca-tion，1988：1-9．

[7]郜舒竹.释“比”[J].教学月刊·小学版（数学），2021（6）：4-8．

[9]王延霞，李鹏，邓岳川，等.基于布鲁姆教育目标分类法的课程持续改进研究[J].榆林学院学报，2022（2）：59-63．

[10]ALEXANDERHB.LivingMind：Aninquiryintothepsychologicalandlogicalfoun-dationofhumanunderstanding[J].ThePluralist，2008（1）：11-88．

[11]姚建欣，郭玉英.为学生认知发展建模：学习进阶十年研究回顾及展望［J］.教育学报，2014（5）：35-42．

[12]吴颖康，邓少博，杨洁.数学教育中学习进阶的研究进展及启示［J］.数学教育学报，2017（6）：40-46．

【本文系北京市教育科学“十三五”规划2020年度一般课题“运用大观念发展儿童关键数学能力的实践探索”（立项号：CDDB2020140）的阶段性研究成果】

（作者单位：北京教育科学研究院，北京小学丰台万年花城分校）H