基于决策树模型的黄河水沙变化预测

摘 要：本文基于小浪底水库下游黄河某水文站2016—2021年的水流量与含沙量的实际监测数据，分别建立随机森林（Random Forest）、决策树（Decision Tree）和极端梯度提升（XGBoost）3种机器学习回归模型预测水流量和含沙量的走势，并对比3种模型的拟合效果。结果表明，与随机森林和极端梯度提升算法相比，决策树算法对水沙变化的预测效果更好，其能够有效拟合水沙变化的走势，对未来黄河流域的水沙治理有一定参考价值。

关键词：应用统计数学；小浪底水库；水沙变化；决策树模型；机器学习回归预测

中图分类号：O 213" " 文献标志码：A

黄河是中国最大的泥沙河流，其水沙混悬的特性使其容易形成堆积和淤积，增加洪水暴发的风险[1]，通过研究黄河水沙的季节性和周期性变化规律，预测未来水沙的变化情况，可以帮助优化水资源的分配和利用，从而减少河道的淤积，提高河道的输水能力，降低洪水灾害发生的概率[2]。

随着水利信息化不断发展，大数据技术在黄河调水调沙工程中的应用会越来越广泛，但目前将大数据建模技术应用于黄河的水流量和含沙量预测的研究较少。因此，本文主要基于大数据领域的机器学习模型对2016—2021年的黄河水沙变化的数据进行建模计算，解决水沙变化的长期预测难，预测精度不高的问题。

1 研究区域与方法

1.1 研究区域

黄河小浪底水利枢纽工程是黄河干流上的一项重要综合性水利工程，位于河南和山西交界处，库区长度为130km，总面积为278km2。它是黄河中游最后一段峡谷出口，并且是黄河干流三门峡以下唯一具有较大库容的控制性工程。

1.2 研究方法

1.2.1 三次样条插值法

三次样条插值法是一种常用的数值插值技术，它的目标是通过一个分段的三次多项式函数来逼近数据点，以便在每个数据点处都能得到平滑的插值结果。分段就是把区间[a，b]分成n个区间 [（a，x1），（x1，x0），...，（xn-1，b）]共有n+1个点。每个小区间的曲线是一个三次方程Si（x）=ai+bix+cix2+dix3，三次样条方程满足以下条件[3]。1）在每个分段小区间[xn-1，xn]上， S（x）=Si（x）" 都是一个三次方程。2）满足插值条件，即S（xi）=yi，（i=0，1，...，n） 。3）曲线光滑，即S（x）、S'（x）、S\"（x）连续。

1.2.2 决策树算法

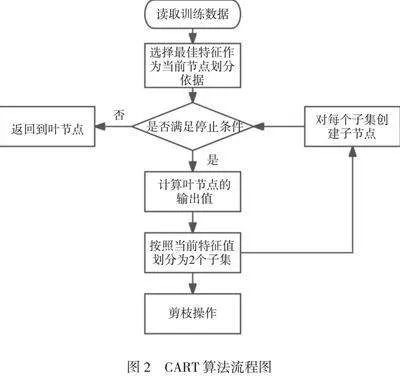
决策树算法是一种有监督的机器学习方法，适用于回归和分类任务。该算法通过树状结构将数据集分成具有相似特征的不同子集。每个内部节点代表一个属性/特征，每个分支代表该特征的一个可能取值，而每个叶子节点对应一个类别标签或是用于预测的数值。算法通过数据的属性特征进行递归划分，直至满足某个条件停止分裂。这种分裂方法构成了树状结构（如图1所示），使模型易于理解、解释和可视[4]。

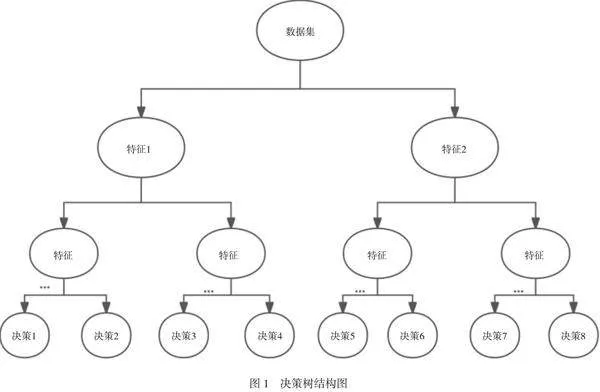
这里仅简单介绍一下所用到的决策树模型CART算法。CART（Classification And Regression Tree）算法是一种既可用于分类又可用于回归的决策树算法。在分类树中，决策树的输出是样本的类别；而在回归树中，决策树的输出是一个实数值。这种灵活性使CART算法可以同时应用于分类和回归任务。而本文使用的是CART算法的回归树部分，其算法流程如图2所示[5]。

算法流程如下。1）选择最优切分特征j和切分点s，如公式（1）所示。遍历所有特征的所有可能取值，找到最优的划分特征和划分点。2）用选定的特征j和切分点s对（j，s）划分区域并决定相应的输出值，如公式（2）所示。公式（1）按照切分点将数据分成2个节点，公式（2）求每个节点的均方误差之和。3）继续对2个子区域调用步骤1、2，直至满足停止条件。4）将输入空间划分为M个区域（R1，R2，...，Rm）特征j和切分点s生成决策树，如公式（3）所示。分到相同节点的均值作为预测值，后面的指示函数为划分的区域。

（1）

式中：yi为数据集中第i 个样本的响应变量；c1 和c2分别为R1（j，s）和R2（j，s）的样本输出均值。

（2）

式中：x（j）为在数据集中第j 个特征值；cm为区域Rm中所有样本的目标变量y的均值；Nm 为区域Rm内的样本数量；m可以是1或2，对应左右2个子集[6]。

（3）

1.3 随机森林算法

随机森林是一种有监督机器学习方法，其以决策树为基学习器，并通过集成方式构建。它引入了随机性来提高模型的抗过拟合和抗噪能力。随机森林从样本选取和特征选择2个角度来体现其随机性[7]。

1.3.1 随机选取样本

在随机森林中，每棵决策树的训练样本集都是通过Bootstrap策略从原始数据集中有放回地抽取和重组形成的，形成了与原始数据集等大的子集合。这意味同一个子集中的样本可以重复出现，不同子集中的样本也可以重复出现。

1.3.2 随机选取特征

与单个决策树在分割过程中考虑所有特征并选择最优特征来进行分割不同，随机森林通过在基学习器中随机考察一部分特征变量，并在这些特征中选择最优特征来进行分割。特征变量的随机性使随机森林模型的泛化能力和学习能力比单个决策树高。

1.3.3 随机森林的算法步骤

步骤1：从原始样本集中使用Bootstraping方法有放回地抽取n个训练样本，进行k轮抽取，得到k个训练集（k个训练集之间相互独立）。

步骤2：针对每一个训练集，构建一个决策树模型，共得到k个模型。

步骤3：针对分类问题，将上述k个模型采用投票的方式得到最终的分类结果；针对回归问题，计算这些模型的均值作为最后的结果。

1.4 极端梯度提升算法

极端梯度提升算法（XGBoost）是一种基于梯度提升树的机器学习算法，被广泛应用于分类和回归问题。它通过迭代训练多个弱学习器，并将它们组合成一个强大的模型[7]。XGBoost的目标函数如公式（4）所示。

（4）

式中：yi为样本真实值；为样本预测值；" l（yi，） 为反应yi与两者的损失函数；n为样本数；Ω（fj）为正则项，用于控制模型的复杂度，避免过拟合；fj为第 j个数的模型；m为分类回归的个数。

通过在正则化函数中添加惩罚项来控制模型训练中的过拟合问题，正则项定义如公式（5）所示。

（5）

式中：T为叶子节点总数；wj为叶子j的权重；γ和λ为模型惩罚系数。

1.5 模型的评价指标

本文根据均方误差（MSE）、均方根误差（RMSE）、平均绝对误差（MAE）、平均绝对百分比误差（MAPE）以及可决系数R2来综合评价模型的优良性[8]。

均方误差（MSE）、均方根误差（RMESE）、平均绝对误差（MAE）、平均绝对百分比误差（MAPE）均是用于评估预测值和真实值的差异程度的一种常见的指标，这些指标值越小，代表模型的预测效果越好。可决系数是用于度量因变量的变异中可由自变量解释部分所占的比例，以此来判断模型的解释能力，其值越接近1表示模型的拟合效果越好。

2 实证分析

2.1 数据预处理

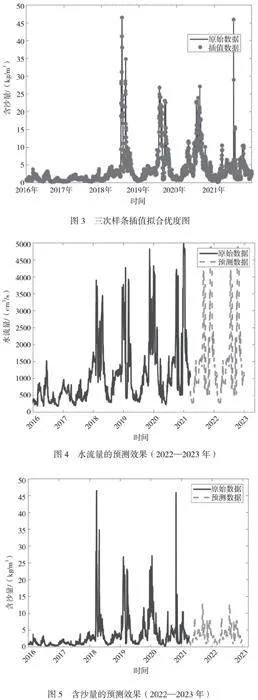
小浪底水库某水文站的2016—2021年的分小时的水流量和含沙量数据一共16735条，含沙量的监测主要在每天的8：00进行，针对2016—2021年每天8：00缺失的含沙量监测数据，运用三次样条插值法进行填充，其拟合图如图3所示。

三次样条插值的拟合图表明，该插值方法对含沙量的填充效果很好，插补数据分布在原始数据的曲线上。

2.2 机器学习模型拟合水沙走势

为了拟合该水文站的水沙走势，本文将历史数据分成2个部分，80%的数据作为训练集训练模型，20%的数据作为验证集验证模型的效果，随后应用模型预测2022—2023年的水流量和含沙量的值。

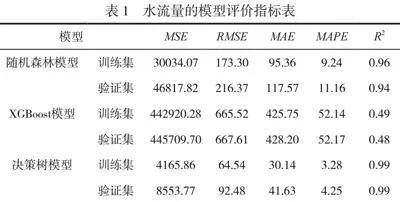
针对水流量，主要监测时刻在每日的0点、4点、8点、12点、16点、20点，因此选取每日的这6个时刻的水流量数据进行建模和预测。3个机器学习模型在训练集和验证集上的评价指标具体见表1。

通过分析上述评价指标表，对比随机森林模型和XGBoost模型，决策树模型的拟合效果最好，其对水流量的拟合度在训练集和验证集上均达到了99%。绘制2022—2023年的预测值走势图，如图4所示，折线是2016—2021年每日的水流量的真实数据，虚线是决策树模型计算的2022—2023年的水流量的预测数据。可以看到模型能很好地捕捉水流量的周期性变化规律，并对未来长达2a的变化规律有很好的预测效果。

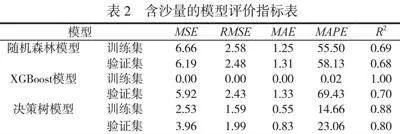
针对含沙量，选取其每天8：00的数据进行建模和预测。3个机器学习模型在训练集和验证集上的评价指标具体见表2。

通过分析上述评价指标，对比随机森林模型和XGBoost模型，决策树对含沙量的拟合效果最好，其训练集上的拟合优度R2为88%，验证集的拟合优度R2达到了80%，虽然XGBoost模型在训练集上的拟合优度高达100%，但其在测试集上的拟合优度仅为70%，模型的泛化性较差，因此最终选择决策树模型来预测未来2a的含沙量走势。绘制2022—2023年的含沙量的预测值走势图，如图5所示，蓝色折线是2016—2021年每日的含沙量数据，虚线是决策树模型计算的2022—2023年的含沙量的预测数据。可以看到模型能很好地捕捉到含沙量的周期性变化规律，并对未来长达2a的变化规律有不错的预测效果。

3 结语

为了更准确地预测未来2a黄河中游水沙通量的变化趋势，本文首先分析了2016—2021年水沙通量的周期性和季节性变化规律，随后建立3种经典的机器学习模型进行对比分析，结果表明决策树模型对水流量的拟合度为99%，对含沙量的拟合度为80%，且该模型能够有效预测未来2a的水沙变化的趋势，解决了预测周期长会导致预测精度不高的难题。

参考文献

[1]胡春宏.黄河水沙变化与治理方略研究[J].水力发电学报，2016，35（10）：1-11.

[2]陈俊卿，范勇勇，吴文娟，等.2016—2017年调水调沙中断后黄河口演变特征[J].人民黄河，2019，41（8）：6-9，116.

[3]于洋，袁健华，钱江，等.新边界条件下的三次样条插值函数[J].软件，2016，37（2）：25-28.

[4]王明红.基于对数加法模型看产险公司保费收入的季节性效应及未来保费预测——以2008-2018年时间序列数据为例的实证分析[J].保险职业学院学报，2019，33（4）：61-64.

[5]杨学兵，张俊.决策树算法及其核心技术[J].计算机技术与发展，2007（1）：43-45.

[6]杜小芳，陈毅红，王登辉，等.大数据平台上的并行CART决策树算法[J].西华师范大学学报（自然科学版），2021，42（2）：196-201.

[7]吴新，邓晓青.黄河干流缺水决策树模型研究[J].人民黄河，2007，（6）：25-27，80.

[8]周志华.机器学习：第1版.[M].北京：清华大学出版社，2016.

[9]司守奎，孙玺菁.数学建模算法与应用[M]北京：国防工业出版社，2011.

作者简介：崔春林（1994—），女，重庆，讲师，硕士学位，重庆城市管理职业学院，主要研究方向为应用统计、机器学习。