基于BOPPPS教学模式培养数学思维的高等数学教学设计

摘要：文章以高等数学中的导数概念为例，探究基于BOPPPS教学模式的教学设计，以学生为中心，引导学生通过生活实例理解导数概念产生的背景，同时以简单到复杂、陌生到熟悉的数学思维与分析特例的基本科学分析方法，由实际问题（教师引导）—数学问题（自主分析）—数学模型（自主分析与教师点拨）知识层层升阶，通过BOPPPS教学模式，从知识、能力、素养三个方面实现导数概念教学目标的达成度。

关键词：导数概念；BOPPPS教学模式；教学思维

一、研究背景

通过高等数学课程教学，教师可以培养学生的抽象思维能力、逻辑推理能力、空间想象能力；培养学生熟练的运算能力和综合运用所学知识分析和解决问题的实践应用能力；培养学生学会建立数学模型，具备用数学方法解释自然规律的科学思维。但高等数学涉及的概念、定理、公式、结论较多，要求学生具备严密的逻辑思维能力，因此高等数学课程教学研究很有必要。

第一﹐高等数学授课内容繁多且知识的应用背景比较陈旧，学生在有限的时间内须掌握的知识较多，且所学知识与实际生活几乎脱节。第二，教师大多按照“定义—定理—证明—推论—例题—练习”的套路授课，授课模式单一，缺乏精心设计，学生难以集中注意力，且终结性评价“重结果、轻过程，重知识、轻能力”，强调通过考试评价学生的学习效果，不利于调动学生学习的积极性。第三，学生被动接受知识，很难真正参与学习，自主学习能力弱，同时师生之间、生生之间缺乏互动交流与思维的碰撞。为有效解决高等数学教学中存在的问题，教师要在教学中改进教学模式。

二、BOPPPS教学模式

BOPPPS教学模式将课程流程分解为六个部分：导言、学习目标、前测、参与式学习、后测、总结，以六个环节的英文首字母命名，各部分之间环环相扣。BOPPPS教学模式的教学框架如下。首先，引出教学内容，作为课堂的开端，引入方式新颖有趣，激发学生的学习兴趣，并明确学习目标，掌握学习方向。其次，基于前测，诊断评价，了解学生的知识基础，做到因材施教，并及时调整教学计划。在教学中，学生处于主体地位。在该环节中，教师通过设置教学活动促进师生之间、生生之间进行互动。最后，检测学习效果，有效评价教学过程，并系统概括知识点，厘清学习框架。

BOPPPS教学模式六个环节之间紧密联系，其完整的教学框架为教师的教学过程作出了指导，使教师的教学设计具有较强的针对性和实用性。BOPPPS教学模式在教学方法上以学生为中心，要求学生主动参与学习，并及时获得学生的反馈信息，调整后续教学环节，促进教学目标的顺利达成，培养学生的自主学习能力。

三、基于BOPPPS教学模式的导数概念教学设计

导数概念是高等数学的基础性内容，之前学生已学习函数极限等相关内容，之后将学习偏导数等相关内容，因此导数概念在高等数学这门课程中起着承上启下的作用。同时，学生对导数的掌握程度对后期专业课程的学习也具有重要的影响。因此，导数概念不仅是学生理解、掌握微分和不定积分内容的基础，还为学好后期数学课和专业课的重要铺垫，更是学生今后继续深造的重要基础。

（一）BOPPPS——B（导言）

教师创设情境，采用案例式教学方式，播放关于我国高铁的短视频：短片中飞驰的高铁是我国创新能力的标志，也是我国向世界递出的一张名片。中国高铁快且稳，如何从数学的角度来研究高铁的快与稳？教师可以提出具体的数学问题。问题一：高铁在运行的过程中，电子屏清晰地显示了高铁在变速行驶过程中每个时刻的速度，如何求解某时刻的速度？问题二：当高铁驶入弯道时，为保持高铁的平稳运行，弯道的设计会涉及曲线的弯曲程度，如何求解切线斜率？通过上述两个问题，教师引出本节的教学内容：导数概念。

（二）BOPPPS——O（目标）

教师给出本节课的教学目标：第一，掌握函数的导数定义；第二，会求函数在某一点的导数；第三，理解导数的思想与方法。通过以上阶段性小目标的达成，最终帮助学生实现学以致用的目的。

（三）BOPPPS——P（前测）

课前，教师要求学生复习预备知识：极限的基本概念、基本思想与计算，并在学习通发布导数概念课前测试，检测学生对预备知识的掌握情况。

（四）BOPPPS——P（参与式学习）

首先，教师提出问题：变速直线运动的瞬时速度，即设质点运动位置的函数为s=f（t），求t0时刻的瞬时速度。

教师解析问题，引导学生将复杂问题转化为简单问题，将求解瞬时速度转化成求解某时间段内的平均速度。通过师生互动，解决简单问题后，还需要想办法从简单问题的解得出原复杂问题的解，这是本节的难点。为便于学生理解，教师通过动画仿真，让学生观察随着t无限趋近于t0，平均速度无限趋近于瞬时速度。通过对平均速度表达式取t趋近于t0的极限，便可得到t0时刻的瞬时速度。

其次，教师提出问题：平面曲线的切线斜率，即设曲线C：y=f（x），求它在M（x0，f（x0））点处的切线MT斜率k。

对于此问题，教师采用小组合作教学方法，要求学生小组讨论：参考第一个问题，以小组形式讨论第二个问题，并将讨论结果提交至学习通。通过小组合作，教师引导，学生讨论得到切线斜率的求解结果。

以小组讨论形式，能发挥学生的主体作用，提高学生自主探究、合作学习和沟通能力。不仅如此，学生以小组合作学习的方式完成教师安排的任务，能实现“知识、能力、素质”三位一体的教学目标。

通过求解瞬时速度与切线斜率，教师引出这两个问题涉及的理论早在17世纪便由英国数学家牛顿和德国数学家莱布尼茨分别在研究力学和几何学中已经建立起来了，由此使得微积分得以迅速发展，这两位伟大的数学家被称为微积分的创始人。教师结合数学文化开展课程思政，融入数学史和数学家故事，通过介绍数学家的科学精神，不仅可以使学生了解更多数学发展史，向学生展示数学文化史与数学发展的关系，而且能促进素质文化教育与人文素质教育的结合。

最后，教师顺着数学家的生平事迹，一起探索导数的奥秘：通过让学生观察瞬时速度与切线斜率表达式的共性“差商的极限”，将具体问题抽象化，总结得到函数在某一点处导数的定义；通过归纳抽象得到导数定义，引导学生用理论指导实践，进一步借助导数的定义给出导数的物理意义与几何意义；通过引导学生探究导数的意义，让学生更加直观地了解导数。

（五）BOPPPS——P（后测）

教师为巩固学生对导数定义的掌握，在学习通平台设置后测问题，检测学生对导数定义的掌握情况，并根据学生对知识点的掌握情况进行适当补充与讲解。

强化练习1：设高铁在运行过程中，其路程与时间的关系为S=2t2+30t-40，求高铁在t=10s时的瞬时速度。

考查要点：通过分析，根据导数的物理意义，将求高铁在t=10s时的瞬时速度转化成函数在t=10的导数。

强化练习2：过山车是一种富有刺激性的娱乐项目，那种风驰电掣、有惊无险的快感让不少人着迷，但设计者必须保证过山车的安全问题。假设其中一段轨道近似满足函数y=f（x）=x4-1.5x2+5，其区间为[0，2]，该轨道在处的陡峭程度是多少？

考查要点：培养学生数学建模的能力，将实际问题转化为数学问题并求解。通过分析，根据导数的几何意义，将求轨道在x=1处的陡峭程度转化成函数在x=1的导数。

（六）BOPPPS——S（总结）

通过学习，学生初步认识什么是导数，导数是如何计算的。在导数概念教学过程中，教师要有意识地引导学生转变思维，以学生既有知识为基础，唤醒学生的知识记忆，并进行相应拓展和提高，帮助他们全面认识、理解所学内容，学会应用导数解决相应问题。

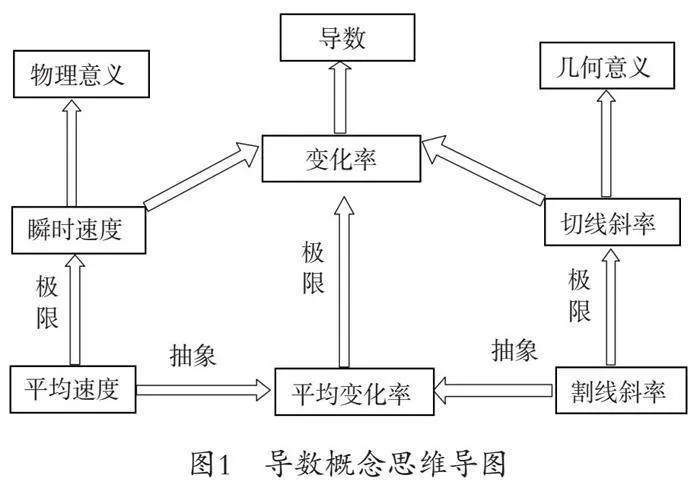
本节课通过链接旧知——极限思想，由平均速度得到瞬时速度，由割线斜率得到切线斜率，将平均速度与割线斜率抽象得到平均变化率，对平均变化率取极限便得到变化率，由此得出本节课的核心内容：导数概念。教师通过建构知识结构，加工整理数学概念，帮助学生深入理解数学知识。教师和学生共同给出导数概念的思维导图，通过思维导图让学生建立知识点之间的关联，进一步从知识、能力、素养三个方面，检验导数概念的教学目标是否达成，最后通过布置线下作业与线上作业引导学生自主学习，巩固导数概念。导数概念思维导图如图1所示。

四、结论

教师基于BOPPPS教学模式讲解导数概念，能让学生在导数概念的学习过程中充分发挥主观能动性和主体作用。学生在课前和课后通过小组合作的方式，依托网络教学平台的数字资源、教学公众号和数学软件形成教学闭环，环环相扣，实现自主学习、互助学习、思想碰撞，随时随地、多维度地学习、交流，以较好地解决本节内容的重点和难点。

例如，教师可以通过“中国高铁快又稳”的案例，激发学生内心的民族自豪感和爱国热情；通过图片－动画－仿真对导数的重点和难点内容进行分析，构建学生的空间感；通过教材与文献对导数的不同分析，促进学生辩证思维与质疑精神的养成；通过“中国速度——高铁快又稳”引出瞬时速度与切线斜率以及过山车的陡峭程度，引导学生运用数学的思维方式观察、分析、解决日常生活的问题。

参考文献：

[1]李正波，刘琼.基于学生中心理念的BOPPPS混合式教学模式改革研究[J].教育信息化论坛，2023（11）.

[2]刘琼.《高等数学》课程思政建设的探索与路径[J].生活教育，2022（10）.

[3]徐福江.高校应用BOPPPS教学模式的问题与对策[J].宿州教育学院学报，2022（10）.

[4]杨昆，石晓梅，郭睿.0-PIRTAS翻转课堂结合TBL在基础医学课程素质教育中的实践：以“细胞信号转导的分子机制”为例[J].中国生物化学与分子生物学报，2023（3）.

[5]曾生达，廖珊莉，唐国吉.地方师范院校高等数学教学改革与探索[J].广西民族大学学报（自然科学版），2023（8）.

[6]马明月.高等数学中的数学思想及其应用[J].数学之友，2023（4）.

基金项目：茅台学院2023年度教育教学研究与改革项目“基于学生中心理念的‘BOPPPS+学习通’混合式教学模式改革研究”，项目编号：2023001。

（作者单位：茅台学院）