小学生数学核心素养测评指标体系构建

小学生数学核心素养是我国基础教育数学课程改革深化的重要目标，体现了新时代育人理念。借助文献法、德尔菲法与访谈法，形成小学生数学核心素养测评指标体系，其中蕴含4个一级指标和12个二级指标。数学知识包含知识融合、知识理解、知识创新三个指标，数学情感包含数学亲近感、数学认同感、数学审美感三个指标，问题解决包含问题情境、问题表达、问题策略三个指标，数学思维包含思维方式、思维转化、思维联结三个指标，数学知识、问题解决、数学思维可以借助考试评价方式进行测评，数学情感可以借助过程评价方式进行测评。该测评指标体系的构建为小学生数学核心素养考查提供理论框架与观测指标。

数学核心素养测评指标；数学知识；数学情感；数学思维

武丽莎，岳俊冰，朱立明，等.小学生数学核心素养测评指标体系构建[J].教学与管理，2024（36）：64-69.

2022年4月教育部颁布《义务教育数学课程标准（2022年版）》（简称“新课标”），进一步凝练了义务教育阶段学生核心素养，强调数学课程培养学生核心素养包括数学眼光、数学思维、数学语言三大部分内容[1]，称之为数学核心素养。在教学中对学生数学核心素养的评价不能仅仅依赖其构成与表现，清晰的测评指标是有效展开评价的关键。本文聚焦新课标中核心素养的构成及具体表现，借鉴人文社科领域测评指标构建的思路，首先，在文献梳理与专家访谈的基础上提出小学生数学核心素养的相关要素，初步构成测评指标；其次，设计专家咨询问卷，选取数学教育领域中从事数学核心素养相关研究的各个层面群体样本，进行专家咨询，形成测评指标体系；最后，借助层次分析法，对各级各个指标进行权重赋值，形成小学生数学核心素养的测评指标体系。

一、数学核心素养测评的研究基础

1.数学核心素养测评的述评

长期以来，在“双基”和“应试”的影响之下，“分数至上”是我国数学教育评价的基本状况，这种高度追求学生成绩提升的评价，单纯对基础知识与基本技能进行考核，忽视了数学教育中的隐性目标，难以测评学生的能力、情感、态度与价值观，从而导致核心素养评价内容的缺失，而“传授知识”与“培养能力”之争由来已久，将两者合二为一，形成对学生数学核心素养的有效评价，是当前数学教育领域的重要议题。

（1）基于知识的能力测评

该测评强调数学知识是数学核心素养的基本成分，前者对后者的生成产生重要作用，因此，数学核心素养测评重点是通过数学知识学习转化而来的能力评价。例如喻平在分析多种评价模型基础上，借助知识分类理论，根据知识理解、迁移与创新三种形态，对数学核心素养的水平进行划分，据此进行评价[2]。李润洲借助知识的层级结构，结合过程与结果，划分了核心素养的三种形态[3]。

（2）基于情境的测评

该观点聚焦情境在数学核心素养评价中的价值，数学核心素养评价依赖于不同类型、不同复杂程度的问题情境。例如张会杰指出数学核心素养测评要依赖情境，借助科学、合理的任务情境，才能更真实地反应学生数学核心素养的发展水平[4]。常磊等从现实世界情境和纯数学情境出发，指出情境的话题、成分、结构、表征形式、信息容量、开放程度、可容纳的思维活动空间等都会对数学核心素养评价产生密切影响[5]。胡凤娟等通过构建基于情境的案例，从数学核心素养三个水平阐释了高中数学核心素养的测评[6]。

（3）基于新课标的高考测评

该种评价聚焦数学高考内容，侧重在高考内容中对学生核心素养进行测查。例如任子朝等指出数学核心素养的评价既要关注对数学知识进行考核，又要考查知识背后所蕴含的数学思维，还需注重在运用中对核心素养的评价[7]。史宁中等也从高考命题角度出发，强调试题中要对数学核心素养进行测评；在题目编制过程中，一方面要关注对学生数学核心素养考查深度，另一方面要关注对学生数学思维能力的考核[8]。

（4）基于TIMSS和PISA的测评

该种评价基于TIMSS和PISA项目，TIMSS侧重内容与认知，PISA侧重内容、过程与情境[9]，在PISA

2021数学评价中又侧重了推理和问题解决[10]，数学核心素养的评价在一定程度上可以借鉴TIMSS和PISA的测评[11]。例如张维忠等通过对TIMSS历年数学测评框架的内容领域和认知领域的比较与分析，指出数学核心素养评价应借助信息技术，注重学生合作问题解决素养，增加探究性任务[12]。胡典顺等基于PISA测评，指出数学学科核心素养的测评要明确“素养”“问题”“情境”和“知识”四个要素之间的逻辑关系及其在测试中的定位[13]。

通过文献梳理可以看出，从评价对象来看，高中生数学核心素养研究较多，小学生数学核心素养的研究较少；从评价内容来看，数学知识、能力方面的测评较多，数学思维与价值观测评较少，单一维度研究较多，系统研究较少，外显目标评价较多，内隐目标考核较少；从评价方式来看，以纸笔测验为代表的结果性评价较多，过程性评价较少。

2.数学核心素养测评的依据

（1）时代性依据

进入21世纪以来，中国基础教育在不断变革中发生了很大变化，随着教学大纲、考试大纲转变为课程标准，基础教育的改革逐渐演变成对课程标准的修订与实施。2014年，教育部关于《全面深化课程改革落实立德树人根本任务的意见》中提出，要发展中国学生核心素养，在各级各学段构建核心素养体系并进行落实。因此，基于核心素养的课程标准的修订拉开序幕。在“双减”政策背景下，随着新课标的颁布，小学数学课程与教学进入一个新阶段，以核心素养为导向的小学数学教学成为落实立德树人教育根本任务的重要环节。

（2）学理性依据

2003年，经济合作与发展组织的核心素养框架为世界各个国家和地区研制适合各自核心素养体系提供了指引[14]。2018年，教育部颁布的《普通高中数学课程标准（2017年版）》，凝练了数学学科核心素养，标志着核心素养体系从课程标准走向课堂教学。而2022年新课标的颁布，再次实现与高中数学课程标准的对接，体现了数学核心素养的一致性与阶段性[15]。如何确保数学核心素养在评价中有所体现，也是本次新课标修订的重要工作。

（3）方法论依据

从指标构建的逻辑顺序来看，通过文献梳理和专家意见征询，提炼测评指标体系，根据相关研究领域专家建议，对指标整合与增减，通过文本分析法，对数学核心素养关键要素进行词频统计，初步形成测评指标。借助德尔菲法，一方面要对初步形成的测评指标进行验证，另一方面获得各个指标的重要性排序，利用层次分析法，确定测评指标体系权重，提供数据来源。研究注重理论思辨与实证探究的双向结合，通过指标的提取形成对测评指标尽可能全面的描述，借助指标的修订保证测评指标的代表性。

二、小学生数学核心素养测评指标体系构建

1.小学生数学核心素养测评指标的初构

（1）测评指标提取

利用中国知网“高级检索”模式，以“数学核心素养”为检索主题，匹配为“精确”，检索时间为“2014年至2023年”，综合考虑作者与期刊的权威性，选取代表性文献进行分析。通过上述梳理发现，数学知识、数学思维、数学能力、数学情感等是学生数学核心素养的重要成分[16]。测评指标的提取旨在更全面地获取数学核心素养的要素信息，借助开放性归纳，通过文献述评与专家访谈，对小学生数学核心素养测评指标进行研判，分析核心期刊所发表的数学核心素养的核心词，并对其进行词频分析。关于数学核心素养的核心词主要包括数学知识（17.4%）、数学技能（8.3%）、数学思想（5.5%）、数学思维（4.6%）、数学关键能力（11.9%）、数学品格（5.5%）、数学情感（9.2%）、数学经验（6.4%）、表达交流（7.3%）、问题解决（12.8%）、数学精神（8.3%）、数学态度（2.8%）。

（2）测评指标修订

为了保证小学生数学核心素养测评指标更加精炼并具有代表性，根据上述关键词编制专家问卷，采用李克特量表形式，每个问题设置非常认同、多半认同、一半认同、多半不认同、非常不认同5个选项，由于是对专家认同度的调查，因此问卷中的问题全部是正向题[17]，测评题项平均得分越高，说明专家群体对该指标认同度越高。问卷征求了33位从事数学教育研究的专家和教师的建议，包括从事数学教育或核心素养研究的高校专家9位（这9位专家中有2位是新课标修订组成员），小学数学教研员8位，小学数学教师16位。

结合题项的平均得分，通过对一些专家和教师的访谈，可以将专家建议大体可以分为两类：第一类是针对各指标之间的关系，即指标之间的关系需要尽可能相互独立，避免一些指标在内容上出现包含、重复的现象。有专家指出：“数学知识既有对数学学科知识本身的理解，包括其中的概念和性质，也可以包含学生自己定义的相关命题，在这个定义过程中，就涵盖了数学交流和数学表达，除此以外，在数学交流中，也有学生思维的体现，因此上，数学交流是可以放入数学知识和数学思维之中的。”也有专家指出：“数学技能、问题解决和数学关键能力之间的关系存在交叉重叠，小学阶段应更强调对问题的解决能力，这是关键能力更直接的体现，都是为了问题解决。”第二类是针对测评指标的代表性，即测评指标应集中体现数学核心素养的基本内涵，例如专家指出：“测评指标不宜过多，应重点体现数学核心素养的知识与技能、问题解决能力、数学思维能力等方面，因此可以考虑将数学态度、数学精神与数学情感整合，数学关键能力、推理能力与问题解决整合，将数学知识与数学技能整合为数学双基。”

结合专家问卷得分与访谈结果，从平均分、标准差、变异系数进行分析（见表1）。小学生数学核心素养关键词的平均分在3.177～4.581之间，其中数学关键能力、数学品格、运算思维、数学精FRfCBFnNhDc2BmLc6SLT3P08kELYqlESPi5ApbvlJmk=神、数学态度的平均分低于3.75（5分量表的75%等级值），根据专家建议进行修改与调整。标准差在0.568～0.944之间，均小于1，这表明专家群体建议相对集中，变异系数在0.119～0.276之间，均小于0.5，这表明专家对小学数学核心素养的关键词协调程度较高。基于以上分析，对指标进行重新整合，将15个指标调整为7个，分别是数学知识、数学技能、数学思维、数学情感、问题解决、数学经验、数学交流。

2.小学生数学核心素养测评指标的验证

（1）探索性因素分析

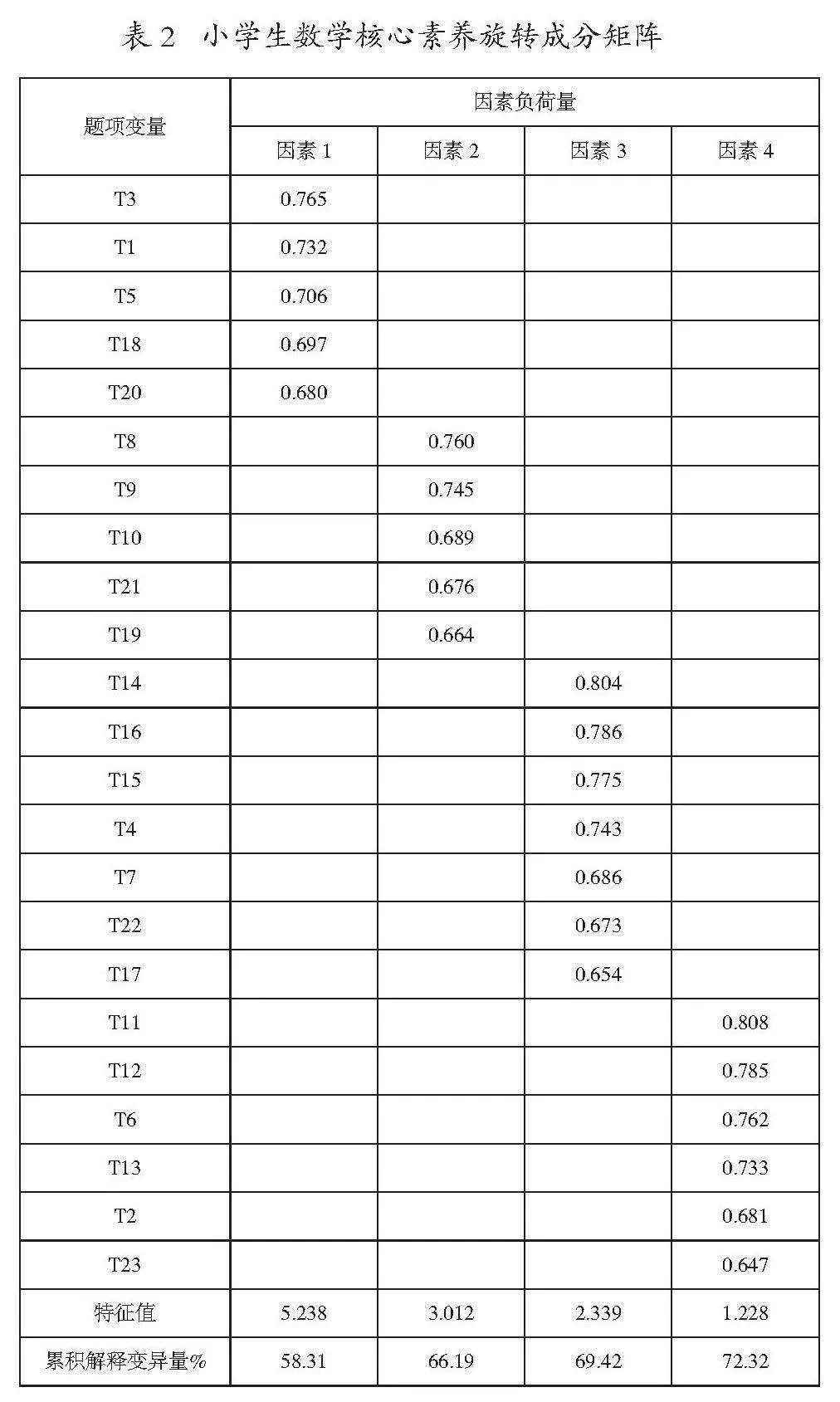
针对数学知识、数学情感、数学技能、问题解决、数学思维、数学经验、数学交流七个一级指标进一步划分二级指标，针对二级指标组织唐山市、长春市、天津市专家编制测试题，经过两次修改与调整，最终形成23个题项的测试卷，其分布见表2所示。在唐山市、长春市、深圳市、承德市4个城市选择学校样本，按照优质学校、中等学校与薄弱学校选择，综合考虑可行性与代表性，每个城市选3所学校，以四年级学生为样本，之所以选择小学四年级学生，是因为四年级属于第二学段，具备一定的知识基础，同时又没有升学压力，能够较好地完成测试，从而获得更真实的数据。采用线上与线下结合方式，共发放问卷825份，收回793份，回收率为96.1%，有效问卷746，有效率为94.1%，将数据分为两部分，随机选取一组用于探索性因素分析，另一组用于验证性因素分析。探索性因素分析中，数学知识、数学技能、数学情感、问题解决与数学经验包含3个题项，数学思维与数学交流包含4个题型。

通过探索性因素分析得到以下结果：第一，得到4个主成分，这表明由原来7个测评指标，降为4个；第二，数学技能、数学经验与数学交流被重构，T18、T20与T1、T3、T5构成一个因素，T19、T21与T8、T9、T10构成一个因素，T4、T7、T17、T22与T14、T15、T16构成一个因素，T2、T23与T6、T11、T12、T13构成一个因素（见表2）。至此，小学生数学核心素养测评指标分别命名为：数学知识、数学情感、问题解决、数学思维。

（2）验证性因素分析

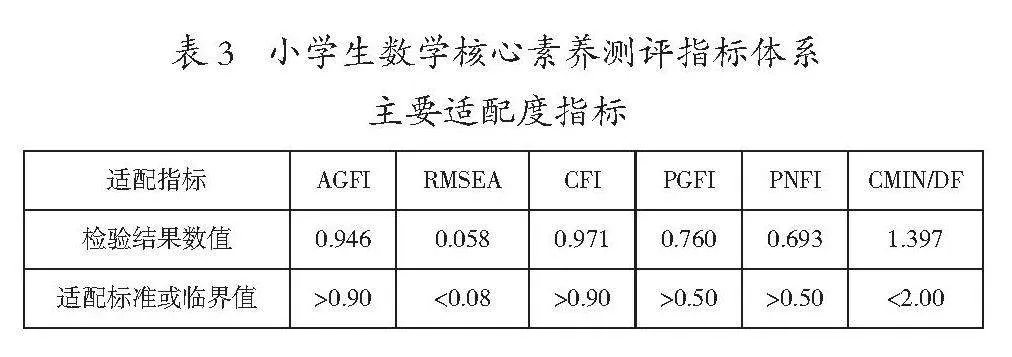
利用AMOS24.0对另一组数据进行验证性因素分析，四个测评指标的因素负荷量在0.65～0.89之间，均大于0.5，这表明模型基本适配度良好。从表3可以看出，AGFI值等于0.946>0.900，RMSEA值等于0.058<0.08（RMSEA值若<0.05为优良，若<0.08为良好），表明绝对适配度指数符合标准；指标CFI的值为0.971，大于0.900，表明增值适配度指数符合标准；PGFI值等于0.760、PNFI值等于0.693，均大于0.50，卡方自由度的比值（CMIN/DF）为1.397<2.000，表明简约适配度指数符合标准，总的来说，初步形成的小学生数学核心养测评指标基本适配指标均达到检验标准[18]。

3.小学生数学核心素养测评指标权重确定

（1）构建判断矩阵

选取一位专家的评分，该专家对小学生数学核心素养测评指标见表4所示。

转换成判断矩阵如下：

（2）计算特征向量

将判断矩阵A的每列原元素进行归一化处理：a'■=■，（i，j=1，2，3，4）其中a■为原始数据，对归一后的判断矩阵按行相加，■=■a'■（i=1，2，3，4），计算出特征向量W=（w1，w2，w3，w4）T，其中wi=■（i=1，2，3，4），W=（0.129，0.086，0.289，0.496）T，因此，该专家认为数学知识、数学情感、问题解决、数学思维四个一级指标的权重依次为0.129，0.086，0.289，

0.496。

（3）检验相容程度

为了达到数学核心素养测评指标的一致性要求，需要对其权重进行检验，其标准如下：CR=■＜0.10时，其中CI=■，λmax=■■，便认为通过相容程度检验，超过这个比值，则需要对指标的权重加以重新修整。以该专家评分为例算，λmax=4.0522，CI=■=0.0174，当n为4时，随机一致性变量RI值为0.90，CR=■=■＜0.10，因此，认为该专家在四个一级指标权重的判断上满足一致性要求[19]。

4.小学生数学核心素养测评指标的阐释

遵循以上程序，分别对其他32位专家的评分进行验证与分析，其中有8位专家未通过相容程度检验，通过对符合检验标准的25位专家数据进行计算，得出小学生数学核心素养一级指标权重的平均数，见表5所示。小学生数学核心素养的数学知识、数学情感、问题解决、数学思维最终权重值依次为0.19，0.11，0.26，0.44。对小学生数学核心素养的二级指标权重值采用同样的方法进行计算并检验，数学知识中知识融合、知识理解、知识创新的权重依次是0.27，0.32，0.41；数学情感中的数学亲近感、数学认同感、数学审美感的权重依次是0.31，0.33，0.36；问题解决中问题情境、问题表达、问题策略的权重依次是0.35，0.27，0.38；数学思维中思维方式、思维转化、思维联结的权重依次是0.24，0.33，0.43。

小学生数学核心素养表达式为C=0.19*K+0.11*E

+0.26*S+0.44*T，其中数学知识表达式为K=0.27*

K1+0.32*K2+0.41*K3，数学情感表达式为E=0.31*

E1+0.33*E2+0.36*E3，问题解决表达式为S=0.35*

S1+0.27*S2+0.38*S3，数学思维表达式为T=0.24*

T1+0.33*T2+0.43*T3，至此，构建了包含4个一级指标、12个二级指标的KEST测评指标体系。

5.小学生数学核心素养测评指标的专家认同度

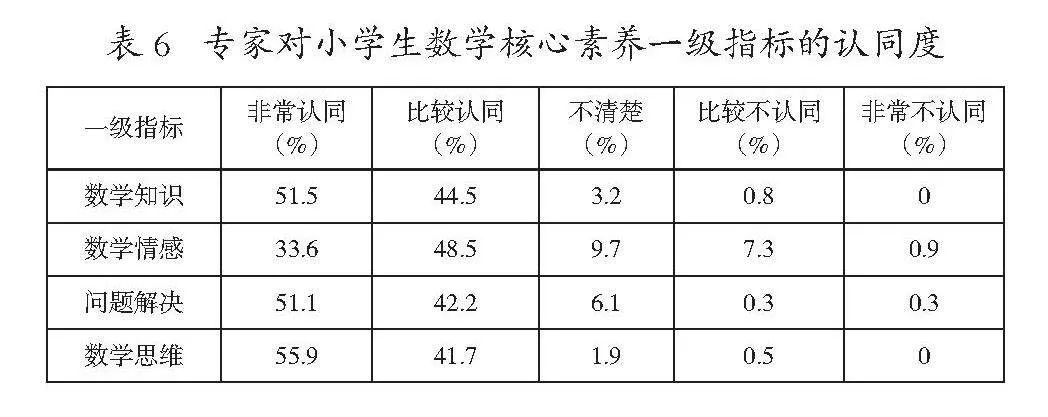
为了检验小学生数学核心素养测评指标的专家认同度，对来自京、津、冀、粤、川、渝、黑、吉、辽、浙等地的12个城镇从事数学教育、数学核心素养研究的231专家教师进行咨询，其中从事数学核心素养研究的专家24位，小学数学教师207位，专家问卷采用李克特五级量表法，认同度包含“比较认同”和“非常认同”两种答案。专家对小学生数学核心素养各测评指标的认同度见表6所示，可以看出，数学知识、数学情感、问题解决、数学思维的认同度依次为96.0%，82.1%，93.3%，97.6%，均超过80%，表明专家对小学生数学核心素养各测评指标认同度较高。专家群体对小学生数学核心素养二级测评指标的认同度在79%～92.1%之间，均超过75%，说明专家群体对测评指标的整体认同度较高。除了数学情感的亲近感与认同感，高校专家与小学数学教师在各测评指标上不存在显著性差异，这表明高校专家与小学数学教师对小学生数学核心素养二级测评指标的协同度较高。

三、研究结论与讨论

1.构建了数学核心素养测评指标体系

本文所构建的学生数学核心素养测评指标体系蕴含数学知识、数学情感、问题解决与数学思维四个一级测评指标，通过层次分析法可以看出，四个一级指标的重要程度为数学思维>问题解决>数学知识>数学情感。数学知识指向了核心素养的知识层面，是数学核心素养的生成根源，包含知识融合、知识理解与知识创新三个二级指标，从重要程度来看，知识创新>知识理解>知识融合；数学情感指向核心素养的态度层面，是数学核心素养的内隐目标，包含数学亲近感、数学认同感与数学审美感三个二级指标，从重要程度来看，数学审美感>数学认同感>数学亲近感；问题解决指向核心素养的能力层面，是数学核心素养的能力体现，包含问题情境、问题表达与问题策略三个二级指标，从重要程度来看，问题策略>问题情境>问题表达；数学思维指向核心素养的思维层面，是数学核心素养的关键内核，包含思维方式、思维转化与思维联结三个二级指标，从重要程度来看，思维联结>思维转化>思维方式[20]。并得到其数学表达式，即数学核心素养＝0.19 *数学知识+ 0.11 *数学情感+ 0.26 *问题解决 + 0.44 *数学思维。

2.数学核心素养测评指标体系的不足

数学核心素养测评指标体系通过理论构建与专家认同度分析，均表现了该测评指标体系具有一定的可操作性，在四个指标中，数学知识、问题解决、数学思维可以借助考试评价方式进行测评。诚然，本文尚存在不足，一方面，后续对学生数学核心素养发展水平进行测量时，数学情感可以借助量表或过程评价方式进行测评，将增值评价引入其中。例如，给学生建立素养考核档案，观察学生的成长记录，侧重考查学生在数学学习前后的变化，而其他三个一级指标需要借助数学问题或数学任务完成测评，而在题目编制过程中，要注重实质，弱化形式，选取能够反映三个指标典型的、代表性的内容设计问题。另一方面，目前构建指标体系所选样本为小学四年级学生，因此，各个指标的权重值是否对其他年级学生也适用需要进一步验证探究。

3.数学核心素养测评指标体系的展望

本文形成对学生数学核心素养测评的分析框架，但是如何借助此框架对学生的数学核心素养实然水平进行测量，并在大数据样本测查下探索学生数学核心素养的发展指数，今后将参考相关教育测评中根据测评指标编制试卷的研究，在测评指标指导下，编制各个二级指标的分测试题目[21-23]，继续对学生数学核心素养发展水平进行研究。此外，当我们可以对学生数学核心素养进行测量时，接下来将更关注的是基于核心素养的教学与课程标准之间的一致性问题，数学教师在教学中蕴含的数学核心素养与课程标准中具体要求的吻合程度是多少，指向核心素养的教学与课程标准一致性的基本特征和影响因素是什么，都是后续值得关注的研究。

参考文献

[1] 中华人民共和国教育部.义务教育课程标准（2022年版）[S].北京：北京师范大学出版社，2022：5-6.

[2] 喻平.数学核心素养评价的一个框架[J].数学教育学报，2017，26（02）：19-23.

[3] 李润洲.学科核心素养的培育：知识结构的视域[J].教育发展研究，2018，38（Z2）：43-49.

[4] 张会杰.何以谓之“好”：核心素养本位测试题的关键特征——基于一道争议数学题的分析[J].中国考试，2018（11）：58-61.

[5] 常磊，鲍建生.情境视角下的数学核心素养[J].数学教育学报，2017，26（02）：24-28.

[6] 胡凤娟，保继光，任子朝，等.高中数学核心素养测评案例研究[J].中国考试，2017（11）：10-16.

[7] 任子朝，陈昂，赵轩.数学核心素养评价研究[J].课程·教材·教法，2018，38（05）：116-121.

[8] 史宁中，林玉慈，陶剑，等.关于高中数学教育中的数学核心素养——史宁中教授访谈之七[J]. 课程·教材·教法，2017，37（04）：8-14.

[9] OECD. PISA 2015 Assessment and Analytical Framework：Science， Reading，Mathematics and Financial Literacy[M].Paris：OECD Publ-

ishing，2016：25-39.

[10] 曹一鸣，朱忠明.变与不变：PISA2000-2021数学测评框架的沿革[J].数学教育学报，2019，28（04）：1-5.

[11] 朱立明.数学学科核心素养高考测评与课程标准一致性分析框架的实证研究[J].教育科学，2021，37（03）：52-60.

[12] 江漂，张维忠.TIMSS数学测评变化及其对我国数学核心素养测评的启示[J].当代教育与文化，2022，14（02）：22-28.

[13] 胡典顺，雷沛瑶，刘婷.数学核心素养的测评：基于 PISA 测评框架与试题设计的视角[J].教育测量与评价，2018（10）：40-46+64.

[14] RYCHEN D S，SALGANIK L H.Key competencies for a successful life and a well-functioning society[M].Cambridge，MA：Hogrefe & Huber，2003：43.

[15] 李俊堂.跨向“深层治理”——义务教育新课标中“跨学科”意涵解析[J].四川师范大学学报（社会科学版），2022，49（04）：116-124.

[16] 朱立明.高中生数学学科核心素养测评指标体系的构建[J].教育科学，2020，36（04）：29-37.

[17] 喻平，赵雅静.数学核心素养中品格与价值观的评价指标体系建构[J].课程·教材·教法，2020，40（06）：89-95.

[18][19] 吴明隆.结构方程模型：AMOS的操作与应用[M].重庆：重庆大学出版社，2009：236-237.

[20] 朱立明，秦丹.新课标下小学生数学核心素养的架构研究[J].课程·教材·教法，2022，42（07）：12-18.

[21] 范涌峰，宋乃庆.学校特色发展测评模型构建研究[J].华东师范大学学报（教育科学版），2018（02）：68-78.

[22] 李艳琴，宋乃庆.小学低学段数学符号意识测评指标体系的初步构建[J].教育学报，2016（04）：23-28.

[23] 张辉蓉，刘丹.基于改进的学生学习增值评价的模式构建及应用[J].中国考试，2023（06）：1-10.

[作者：武丽莎（1986-），女，河北唐山人，南京师范大学教育科学学院，博士生；岳俊冰（1990-），男，山西吕梁人 ，天津师范大学期刊出版中心，编辑；朱立明（1986-），男，河北承德人，唐山师范学院教育学院，副教授；陈秀梅（1972-），女，河北唐山人，唐山师范学院教育学院，教授。]

【责任编辑 王泽华】

*该文为河北省社会科学基金一般项目“指向核心素养培养的初中数学课堂教学与课程标准一致性研究”（HB23JY016）的阶段性研究成果