考虑预设偏移值的10kV配电电缆故障定位方法

摘 要：针对现行方法在10kV配电电缆故障定位中的应用存在定位误差较大和置信水平较低的问题，本文提出考虑预设偏移值的10kV配电电缆故障定位方法。以预设偏移值最小为目标建立目标函数，并设定约束条件，建立10kV配电电缆故障定位模型，采用粒子群算法对模型进行求解计算，得到预设偏移值最小的故障距离，实现考虑预设偏移值的10kV配电电缆故障定位。经试验证明，设计方法定位误差不超过2m，定位结果置信水平在0.9以上，在10kV配电电缆故障定位方面具有良好的应用前景。

关键词：偏移值；10kV配电电缆；故障定位；目标函数；粒子群算法

中图分类号：TM 77 " 文献标志码：A

随着现代社会快速发展，电力已成为支撑社会运转的重要基石。而配电电缆作为电力传输的关键环节，其安全稳定运行对保障电力供应的可靠性至关重要。然而，由于电缆运行环境复杂多变，电缆故障时有发生，这不仅影响了电力供应的连续性，还可能造成严重的经济损失和社会影响。因此，准确、快速地定位电缆故障点，对提高电力系统的运行效率、减少故障损失具有重要意义。

张艳霞等[1]提出了基于电磁时间反演的电缆故障定位方法，利用电磁信号在电缆中的传播特征，反演电缆故障具体位置。彭博等[2]提出了基于小波分析的电缆故障定位方法，利用小波分析技术对电缆故障进行特征分析，确定故障距离。虽然这些方法在一定程度上能够实现故障点的定位，但是其受电缆长度、故障类型和波速变化等多种因素的影响，不能保证定位精度。特别是在实际应用中，由于电缆线路参数的不确定性以及测量设备的误差，定位结果往往存在较大的偏差。并且传统方法还存在计算量大、收敛速度慢等问题，难以满足实际应用的需求，为此提出考虑预设偏移值的10kV配电电缆故障定位方法。

1 建立考虑预设偏移值的电缆故障定位模型

1.1 建立目标函数

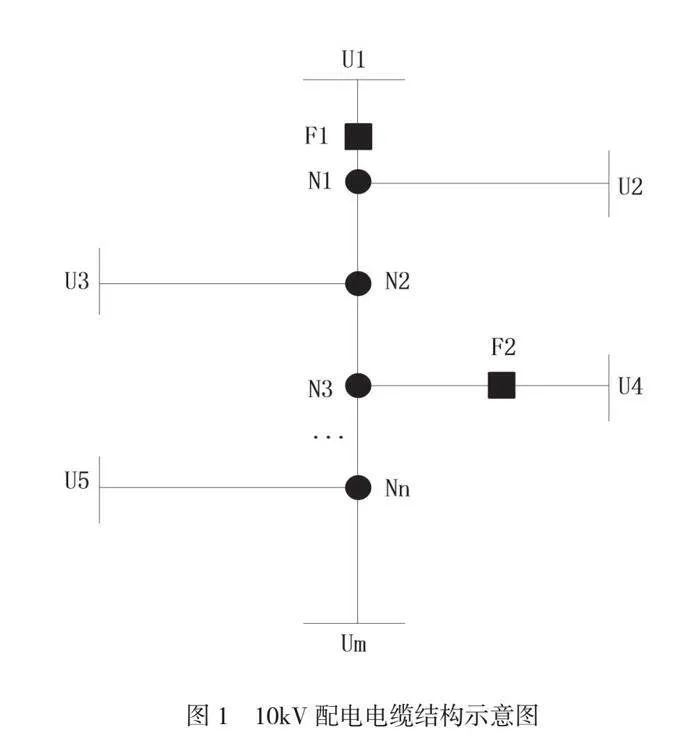
电磁波在介质中具有传播特性，当介质出现中断或者性质发生改变时，电磁波传播速度、波形会发生突变，因此将电缆作为电磁波传播介质，在电缆中传播的电磁波称为行波，根据行波传播原理可知，一旦10kV配电网中的电缆遭遇故障，故障行波会立即从故障发生点出发，沿着线路向各个端点进行传播[3]。为了更清晰地剖析故障行波的传输轨迹，绘制10kV配电电缆结构示意图，如图1所示。

当定位10kV配电电缆的故障位置时，如果预设的故障点与真实的故障点恰好位于同一条支路但位置不同，那么可以采用双端定位算法来确定故障点的具体位置。这种算法会先计算端点（例如电缆的起始端或末端）与其他电缆端点之间的真实故障距离差值，这个差值是通过测量从端点到真实故障点的距离，并减去从端点到该支路线路支点的距离来得到的。同时，也会计算预设故障点与10kV配电线路支点的距离，并通过类似的方式得到端点与其他电缆端点之间的预设故障距离差值。这2个差值之间的差异即真实故障距离差值与预设故障距离差值之间的差异，提供了关于故障点相对于预设故障点位置的重要信息。通过比较这2个差值，并结合电缆的长度和支路的具体情况，可以更准确地推断真实故障点的具体位置[4]。这一差值不仅提供了关于故障位置的重要信息，还有助于更准确地定位故障点[5]。

当构建针对10kV配电电缆故障定位的优化模型时，首先需要定义一系列关键参数，包括电缆的实际长度（设为L）、预设故障点与电缆一端（例如始端）的初始距离估计值（设为dest）、行波在电缆中的理论传播速度（通常基于电缆材质和绝缘层特性，设为vth）[6]以及通过实际测量得到的行波往返时间（设为T）。其次，利用行波传播理论，计算基于预设距离和理论速度的行波往返时间预测值，Tpred=2×dest/vth。通过比较实际测量时间与预测时间的差异，可以计算偏移量，ΔT=|T−Tpred|，进而转换为空间偏移量，Δd=|ΔT/2×vth|。

为了最小化这个偏移量，采用粒子群优化算法来迭代调整dest和vth的值。在粒子群优化算法中，每个粒子代表一个潜在的解决方案（即dest和vth的一组值），并具备自己的位置和速度。算法通过评估每个粒子的适应度（即偏移量Δd的倒数或负数，以最小化问题为目标）来引导粒子群向全局最优解移动。粒子们根据自身历史最优位置及整个群体发现的全局最优位置调整其速度和方向并进行迭代搜索。这种集体智慧与个体经验的结合，有效提升了搜索效率和准确性，直至找到使偏移量极小化的最佳dest和vth组合。

初始时，设定dest=L/2（假设故障位于电缆中点）、vth为电缆制造商提供的典型值。随后，算法开始迭代，每次迭代都根据当前偏移量的正负和大小微调dest和vth，直至满足预设的收敛条件（偏移量小于某一阈值或迭代次数达到上限）。

通过上述过程，建立一个基于优化算法的故障定位模型，精确地确定10kV配电电缆中的故障点位置。

最终，通过优化算法的输出结果，可以获得最佳的预设故障点位置以及行波的传播速率，从而实现对电缆故障的精确定位。

1.2 设定约束条件

结合以上建立的目标函数，对10kV配电电缆故障定位进行约束，设定相应的约束条件。首先，在10kV配电电缆上预设的故障点位置进行约束，预设故障点到端点的距离不能超过电缆长度[7]。其次，行波在电缆上传播的速度不能超出上下限值。将以上设定的约束条件与建立的目标函数整合，组建考虑预设偏移值的电缆故障定位模型，即在约束条件下偏移值最小。

2 电缆故障定位模型求解

采用优化算法对建立的定位模型进行求解，得到预设偏移值最小的预设故障点位置。为了保证优化精度，此次选择粒子群算法对模型进行求解。粒子群算法通过模拟鸟群或鱼群中的行为来进行优化搜索，模拟群体中粒子的行为，每个粒子代表一个目标函数的候选解，并根据其自身的经验和群体的信息进行移动和调整。粒子的位置表示目标函数候选解的特征向量，速度表示粒子在搜索空间中的移动方向和速度，其求解步骤如下。

步骤1：粒子群初始化。假设每一个定位模型中目标函数的候选解为一个粒子个体，组建初始粒子群以及粒子初始移动惯性权重和学习率。

步骤2：定义粒子适应度。粒子适应度值越小，表示电缆上预设故障点位置越接近故障真实位置[8]。因此根据粒子适应度值，选择粒子个体最佳位置和全局最佳位置。

步骤3：粒子位置与速度更新。利用粒子移动惯性权重对粒子移动速度进行更新，如公式（1）所示。根据更新的速度更新粒子个体位置。

vu+1=ωvμ+c[（Xs-xμ）（Ys-xμ）] （1）

式中：vu+1为下一次粒子群迭代粒子移动速度；ω为移动惯性权重；vμ为第μ次粒子群迭代个体移动速度；c为学习率；Xs为选择的个体最佳位置；xμ为第μ次粒子群迭代个体位置；Ys为选择的全局最佳位置。

步骤4：当粒子群迭代次数达到设定上限时，输出适应度值最高的粒子，其对应的解为定位模型目标函数最优解，得到预设偏移值最小的预设故障点，其所在位置为电缆故障位置，以此实现考虑预设偏移值的10kV配电电缆故障定位。

3 试验论证

3.1 试验准备与设计

为了验证本文所提的考虑预设偏移值的10kV配电电缆故障定位方法的泛化能力，以某10kV配电网为试验环境，该配电网采用型号为KHFAS-A5F5的电缆，电缆总长度L为1000m。该配电网含有8个支路，在每个支路上设置故障，故障类型包括短路、断路、绝缘、接地等。故障距离分别为183m、227m、435m、384m、227m、400m、604m、794m。通过试验测量得到的行波在电缆中的传播速度为172m/μs。约束条件设置预设故障点到端点的距离不能超过电缆长度，即不超过1000m。行波在电缆上传播的速度不能超出限值，速度下限为150m/μs，上限为200m/μs。试验在各个支路上安装电磁测量仪，其参数设置如下：采样频率设置为1.25MHz，采样周期设置为0.05s，采样范围设置为1000m×1000m，行波速度范围设置为2.55×105km/s-2.75×105km/s。

试验中共测量行波信号1000个样本，将其代入粒子群算法中对故障定位模型进行求解计算，试验中粒子群算法参数设置见表1。

在粒子群算法的迭代过程中，更新每个粒子的个人最佳位置和全局最佳位置，并更新每个粒子的位置和速度。计算更新后粒子的目标函数值。重复迭代过程，直到达到最大迭代次数或满足其他停止条件，输出全局最佳位置。

3.2 试验结果与讨论

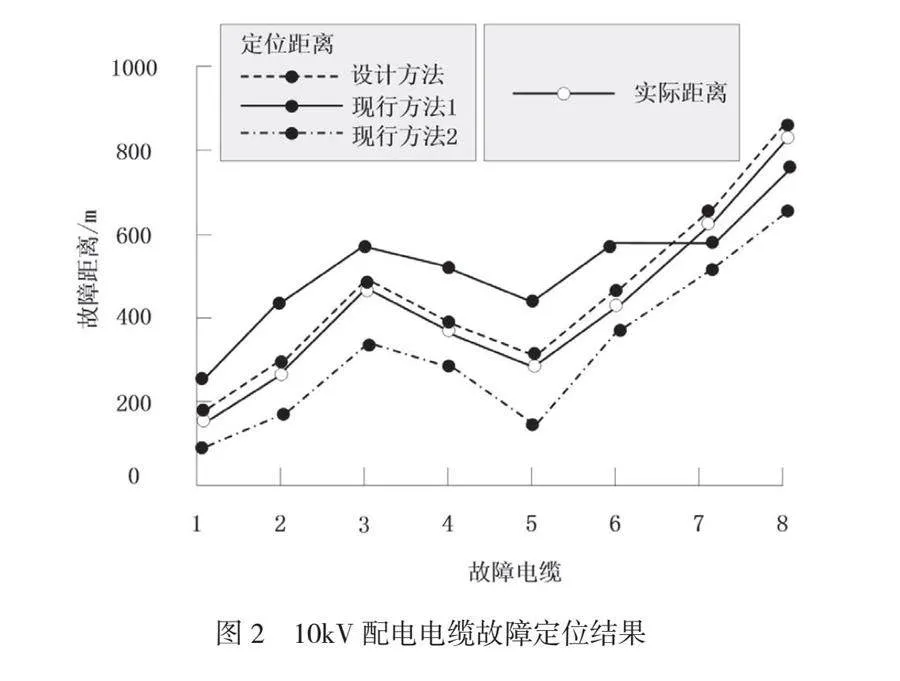
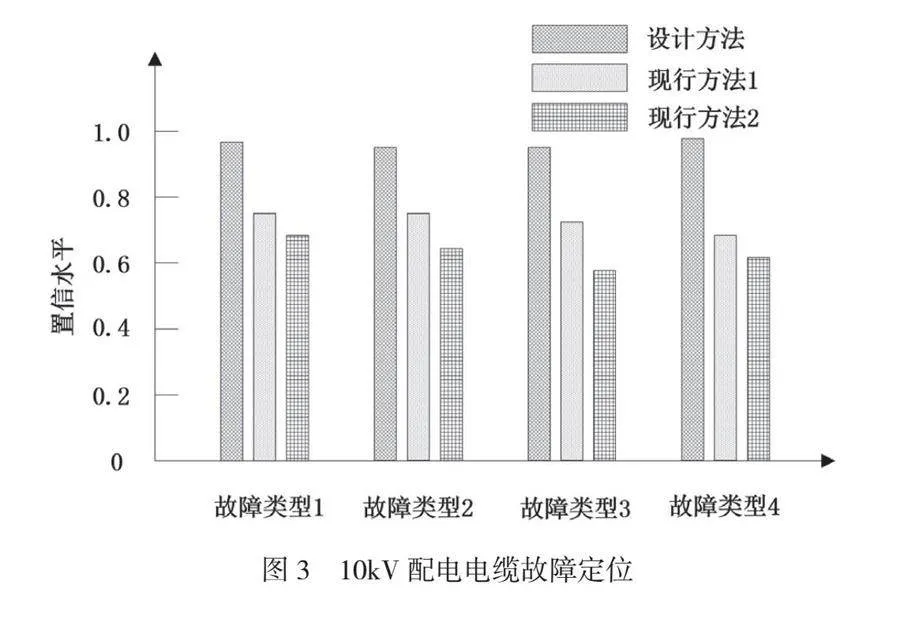
为了使试验数据具有一定的说服性，选择2种主流方法与本文方法进行对比。试验统计了每个支路电缆上故障实际距离与定位距离，定位结果如图2所示。此外，根据统计的故障定位结果，计算3种方法故障定位结果的置信水平，置信水平可以衡量定位结果与实际故障距离的相符程度以及定位结果的可信程度，置信水平取值范围为0～1，数值越高，说明定位结果可信程度越高，定位结果越精准，3种方法故障定位置信水平对比图如图3所示。

由图2可知，采用本文所提方法定位的故障距离与实际距离基本一致，定位误差最高不超过2m，而现行方法1与现行方法2定位故障距离与实际距离差距较大，定位误差远高于设计方法。这是因为当构建10kV配电电缆故障定位模型时，本文所提方法明确设定了以预设偏移值最小化为目标函数。这一目标的设定旨在直接指导优化算法在搜索过程中聚焦于寻找能够使偏移值达到最小的解，即最准确的故障距离。同时，为了确保搜索过程的有效性和解的合理性，还设定了一系列约束条件。这些约束条件对解的取值范围进行了限制，确保算法在求解过程中不会得到无效或不可行的解。这样的设置有助于提高故障定位的准确性和可靠性，使最终得到的故障距离与实际故障位置更接近。

对比图3，本文所提方法定位结果置信水平在0.9以上，基本接近1，而现行方法1定位结果置信水平最高仅为0.78，现行方法2定位结果置信水平最高为0.74，远低于设计方法。这是因为本文所提方法通过设定以预设偏移值最小为目标函数，并结合合理的约束条件，能够精确地指导PSO算法充分利用粒子间的信息共享和协作，同时结合粒子的记忆功能，使算法在搜索过程中能够快速收敛到全局最优解。因此，本文方法具有很高的准确性和可信度。

综上所述，本文所提方法可以将故障定位问题转换为优化问题，简化了故障定位计算，从而保证了故障定位精度。通过以上统计与对比证明，本文所提方法可以实现对10kV配电电缆故障的精准定位，在该方面具有绝对的优势。

4 结语

本文对考虑预设偏移值的10kV配电电缆故障定位方法进行研究，并结合实际案例应用，验证了本文所提方法具有良好的可行性，有效提高了电缆故障定位精度，本文提出的考虑预设偏移值的10kV配电电缆故障定位方法虽然在一定程度上提高了定位精度和稳定性，但仍然存在一些需要改进和完善的地方。此外，随着智能电网建设不断推进和物联网技术快速发展，配电电缆故障定位技术也将迎来新的发展机遇。未来，可以将更多的先进技术引入电缆故障定位领域，例如大数据分析、云计算等，以实现更快速、更准确地故障定位。同时，还应关注电缆故障预防和维护技术的研究，通过提高电缆线路的可靠性和安全性，从根本上减少电缆故障的发生。

参考文献

[1]张艳霞，李婷.基于电磁时间反演的VSC-HVDC系统架空线-电缆混合线路故障定位方法[J].电力自动化设备，2024，44（3）：180-186，224.

[2]彭博，宫士营，李华昕，等.基于小波分析的电力电缆串联谐振耐压试验双端行波故障定位[J].制造业自动化，2024，46（3）：72-75.

[3]黄艺航，蔡凯武，黄晓智，等.基于机器学习的通信电缆故障检测与定位方法[J].自动化与信息工程，2024，45（1）：35-41，60.

[4]刘刚，张圆明，陈晨，等.基于纳秒窄脉冲与时间反演的电缆故障定位系统设计[J].自动化与仪器仪表，2023（7）：170-173.

[5]薛菲，王世民，李霄，等.基于多频带小波变换的电力电缆故障定位方法[J].光源与照明，2023（11）：102-104.

[6]吴吉，唐作鑫，彭向阳，等.基于TFDR波形时域包络线的电缆故障定位技术[J].南方电网技术，2023，17（12）：18-27.

[7]佘建宁，江波，唐玲，等.一种三芯电缆状态在线监测与短路故障定位方法的研究[J].智慧电力，2023，51（11）：91-97，105.

[8]杨明嘉，夏成军，池梓斌，等.基于沿线电流故障分量差值的交叉互联电缆故障测距[J].电力系统保护与控制，2023，51（19）：54-66.