基于改进蝴蝶算法优化LSSVM 的基站移动网络流量预测

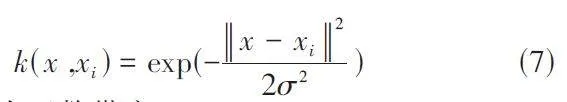
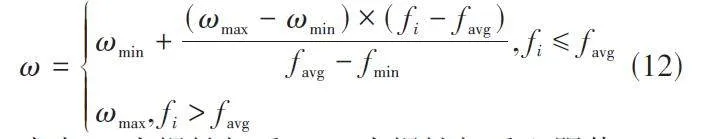
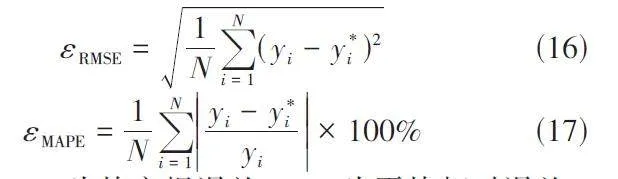
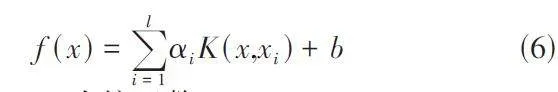
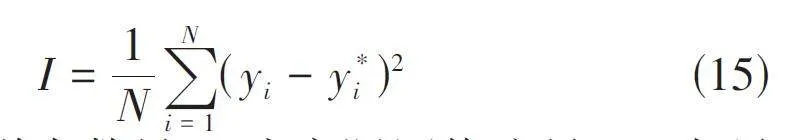
摘要：为提高移动网络流量预测的精度，文章提出了一种基于改进蝴蝶算法（ImprovedButterflyOptimizationAlgorithm，IBOA）优化最小二乘支持向量机（LeastSquaresSupportVectorMachine，LSSVM）的基站流量预测方法。通过引入伯努利映射与自适应调整策略对蝴蝶优化算法进行改进，从而显著增强IBOA算法的收敛性能。利用IBOA算法对LSSVM的两个超参数进行优化搜索，构建了基于IBOA-LSSVM的基站移动网络流量预测模型。通过对某商场的移动网络流量数据进行预测分析，结果表明：IBOA-LSSVM模型的均方根误差与平均相对误差分别为0.243GB和3.89%，IBOA-LSSVM模型在网络流量预测中的效果优于其他对比模型，验证了所提方法的实用性。

关键词：网络流量；预测；最小二乘支持向量机；改进优化蝴蝶算法

中图分类号：TP393文献标识码：A

文章编号：1009-3044（2024）34-0089-03开放科学（资源服务）标识码（OSID）：

随着我国通信基础设施的不断完善，移动互联网技术为人们的生活带来了极大的便利。基站潮汐现象导致基站网络流量负荷出现峰谷现象，若网络资源配置不合理，可能造成网络资源拥堵或配置过剩[1-2]。网络流量预测是解决这一问题的关键[3]，因此有必要研究网络流量预测方法，以提高预测精度。

为准确预测网络流量，专家学者们对网络流量预测方法进行了大量研究。刘洋等人根据移动网络流量数据的时间特性，利用卷积神经网络深入挖掘了网络流量数据的内部特征，在此基础上提出了一种基于深度学习算法的网络流量预测方法，通过实际网络流量预测算力验证了该方法的实用性[4]。汪尧等人将差分进化思想引入灰狼算法，解决了灰狼算法易陷入局部最优的问题，利用差分灰狼算法对支持向量回归机的核心参数进行优化，构建了移动网络流量预测模型，通过算力仿真与对比分析验证了该预测模型的有效性[5]。郑晓亮等人利用改良粒子群算法对自回归差分移动平均模型进行参数寻优，提出了基于新型通信网络的预测方法，该方法不仅能够提升网络流量预测精度，同时也提升了预测结果的稳定性[6]。网络流量数据具有高度非线性的特点，现有模型的预测精度普遍不高，高精度网络流量预测模型还有待进一步研究。

1最小二乘支持向量机

支持向量机（SupportVectorMachine，SVM）是一种经典的非线性拟合方法，而最小二乘支持向量机（LeastSquaresSupportVectorMachine，LSSVM）是在SVM基础上改进而来的，主要用于解决非线性回归与分类问题[7]。与SVM相比，LSSVM主要有两个改进：一是引入了等式约束，二是采用了线性方程组的求解策略。得益于这两个改进，LSSVM不仅继承了SVM的优点，还提高了计算效率。

基于结构风险最小化的原则，可以将LSSVM的优化目标写成下列形式。

对于LSSVM，其优化目标如下：

式中：K（x，xi）为核函数。

核函数的选择对LSSVM的拟合能力至关重要，在众多核函数中，RBF函数具有较强的回归能力，为了提升网络流量预测精度，本文核函数选择RBF函数，其表达式为：

式中：σ为函数带宽。

研究表明，惩罚系数C和函数带宽σ两个超参数的取值对LSSVM的拟合性能影响较大，因此本文采用蝴蝶算法对两个超参数进行寻优。

2改进蝴蝶优化算法

2.1蝴蝶优化算法

2019年，Arora等人深入研究了蝴蝶的觅食和交配行为，提出了蝴蝶优化算法[8]（ButterflyOptimizationAlgorithm，BOA）。在BOA算法中，每只蝴蝶散发不同浓度的香味，种群中的个体根据香味浓度进行局部和全局搜索，不断更新自身位置，最终找到食物。

在蝴蝶种群中，每个个体均会产生不同浓度的香味，蝴蝶在飞行过程中，感知到香味浓度的表达式为：

fi=cIσ（8）

式中：fi为第i只蝴蝶感知到的香味浓度；c为感知系数；I为刺激强度；σ为幂指数，取值范围为[0，1]。

当蝴蝶能够感知到比自身散发的香味浓度更大时，则会展开全局搜索，向香味浓度更大的区域移动，该阶段蝴蝶位置更新公式为：

xt+1i=xti+（r2×g*-xti）×fi（9）

式中：t为迭代次数；xti为第i只蝴蝶在当前迭代时的位置；xt+1i为第i只蝴蝶在下一次迭代时的位置；g*为当前最优位置；r为随机数，取值范围为[0，1]。

当蝴蝶无法感知到比自身散发的香味浓度更大时，则会展开局部搜索，该阶段蝴蝶位置更新公式为：

xt+1i=xti+（r2×xtk-xtj）×fi（10）

式中：xtk为随机选择的第k只蝴蝶在当前迭代时的位置；xtj为随机选择的第j只蝴蝶在当前迭代时的位置。

在BOA算法寻优过程中，全局搜索和局部搜索通常由切换概率p决定，当随机数rand＜p时，算法进行全局搜索，反之进行局部搜索。

2.2BOA算法改进策略

尽管BOA算法原理简单且易于实现，相比传统算法具有更好的优化效果，但在处理复杂函数时，BOA算法可能会陷入局部最优解。为解决这一问题，本文采用伯努利映射和自适应调整策略对BOA算法进行了改进。

2.2.1伯努利映射

种群随机初始化会使初始蝴蝶种群分布不够均匀，影响BOA算法的寻优性能。伯努利映射是一种典型的混沌映射，能够使初始蝴蝶种群分布更加均匀，伯努利映射的表达式为：

xn+1=（2x）nmod1（11）

式中：xn为蝴蝶种群初始位置；xn+1为伯努利映射获得的新位置。

2.2.2自适应调整

BOA算法在迭代前期具有较好的收敛性，但随着迭代次数的增加，蝴蝶产生的香味浓度逐渐减弱，算法收敛性能减弱。为此，本文将惯性权重引入BOA算法，使BOA算法的收敛性能够自适应调整，惯性权重变化公式如下：

式中：ω为惯性权重；ωmax为惯性权重上限值；ωmin为惯性权重下限值；fi为第i只蝴蝶的适应度值；favg为蝴蝶种群的平均适应度值；fmin为最小适应度值。

引入惯性权重后，BOA算法在全局搜索阶段的公式变为：

xt+1i=ω×xti+（r2×g*-xti）×fi（13）

经过上述两种策略的改进，BOA算法的收敛性能得到显著提升，能够实现对复杂函数的优化。

3基于BOA-LSSVM的基站移动网络流量预测模型

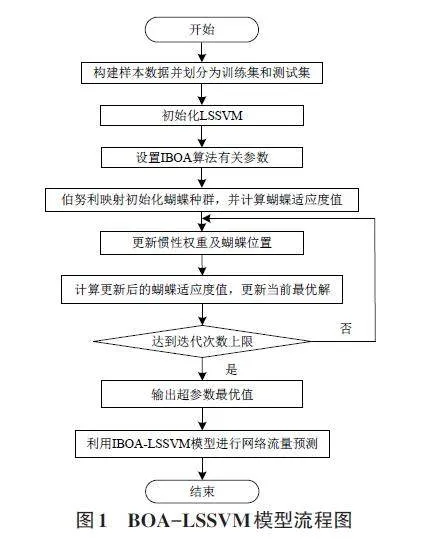
本文采用蝴蝶算法对LSSVM的两个超参数进行优化搜索，构建基于BOA-LSSVM的基站移动网络流量预测模型。图1展示了BOA-LSSVM模型的流程图，主要建模步骤如下。

1）获取连续时间序列上的基站移动网络流量数据，对网络流量数据进行训练，根据训练误差确定其时间序列上的关系，具体如下：

yz=f（yz-m，yz-m+1，...yz-1）（14）

式中；m为嵌入维数；yt为z时刻的网络流量。

2）根据式（14）构建样本数据，将其划分成训练集和测试集。

3）初始化LSSVM，设置两个超参数的初始值和搜索范围。

4）设置IBOA算法有关参数，包括蝴蝶数量、迭代次数上限、感知系数、惯性权重上、下限值等。

5）利用伯努利映射初始化蝴蝶种群，利用式（14）计算蝴蝶适应度值，记录当前最优个体，适应度值计算公式为：

式中，N为样本数量；yi为实际网络流量；yi.为预测网络流量。

6）利用式（12）更新惯性权重，并根据式（13）和式（10）更新蝴蝶位置。

7）计算位置更新后的蝴蝶适应度值，更新当前最优解。

8）判断迭代次数上限是否达到，若是输出超参数最优值，否则返回步骤6）。

9）利用IBOA-LSSVM模型进行网络流量预测。

4算例分析

本文采用某商场连续10天的移动网络流量数据进行仿真分析，数据由当地移动公司提供，采集时间为2023年12月1日至2023年12月11日，采集间隔为30分钟，共获得480组样本数据。样本数据被划分为训练集和测试集，样本容量分别为432组和48组。利用原始LSSVM模型对网络流量数据进行训练，根据训练误差确定时间序列的嵌入维数。训练误差如表1所示，模型训练误差为2.91%。此时对应的嵌入维数为3，由此即可根据式（15）构建样本数据。

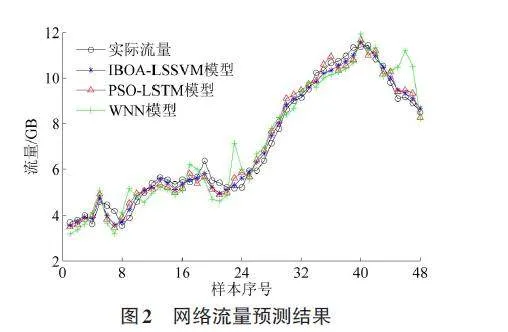
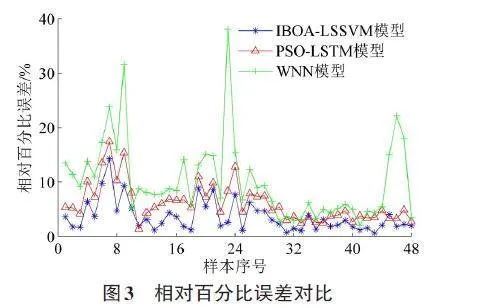
设置IBOA算法参数为：蝴蝶数量为30、迭代次数上限为300、感知系数为0.01、惯性权重上限值为0.9、惯性权重下限值为0.5。将LSSVM的两个超参数C和σ作为IBOA算法的搜索目标，设置C和σ的初始值分别为100和1，搜索范围均设置为[0，1000]。经过迭代计算，最终获得超参数C和σ的最优值为34.75和8L.S3S6V，M由模此型即对可测构试建集IB样O本A-进LS行SV网M络模流型量。预利测用，为IB了OA验-证IBOA-LSSVM模型的有效性，采用PSO-LSTM模型[9]和WNN模型[10]的预测结果进行对比分析，三种模型的网络流量预测结果见图2，预测结果的相对百分比误差如图3所示，结合图2和图3可以看出，IBOA-LSSVM模型预测结果更接近网络流量真实值，误差波动范围也更小。

采用式（16）和式（17）中的两种误差指标对三种网络流量预测模型的预测效果进行评价，具体如下：

式中：εRMSE为均方根误差；εMAPE为平均相对误差。

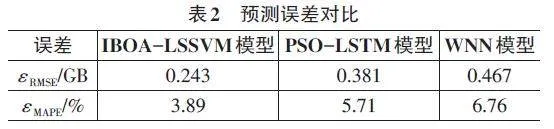
三种模型预测结果的均方根误差和平均相对误差如表2所示，从表2可以看出，IBOA-LSSVM模型、PSO-LSTM模型和WNN模型的均方根误差依次为0.243GB、0.381GB和0.467GB，可见IBOA-LSSVM模型比PSO-LSTM模型和WNN模型具有更好的稳定性；IBOA-LSSVM模型、PSO-LSTM模型和WNN模型的平均相对误差依次为3.89%、5.71%和6.76%，可见IBOA-LSSVM模型比PSO-LSTM模型和WNN模型具有更高的预测精度，综上所述，本文所构基于BOA-LSSVM的基站移动网络流量预测模型的预测效果更好，具有一定的推广和应用价值。

5结论

本文通过引入伯努利映射和自适应调整策略对BOA算法进行改进，得到了收敛性能更强的IBOA算法，并利用IBOA算法对LSSVM进行超参数优化，构建了基于IBOA-LSSVM的基站移动网络流量预测模型。算例分析结果表明，与PSO-LSTM模型和WNN模型相比，IBOA-LSSVM模型具有更好的稳定性和更高的预测精度，验证了BOA-LSSVM模型在移动网络流量预测中的有效性，具有一定的推广和应用价值。

参考文献：

[1]马攀.基于ResNet-LSTM组合模型的网络流量预测研究[J].兰州文理学院学报（自然科学版），2024，38（2）：45-50.

[2]姚立霜，刘丹，裴作飞，等.基于EMD聚类的实时网络流量预测模型[J].计算机科学，2020，47（S2）：316-320.

[3]孟智慧，刘辉，刘伟信，等.基于堆叠长短期记忆网络的互联网流量预测[J].电信工程技术与标准化，2024，37（6）：80-85.

[4]刘洋，廉咪咪.基于深度学习的移动通信网络流量预测方法研究[J].长江信息通信，2024，37（2）：90-92.

[5]汪尧，黄宁，武润升，等.基于改进自回归差分移动平均模型的网络流量预测[J].通信技术，2021，54（12）：2626-2631.

[8]李红岩，王磊，刘宝，等.基于改进蝴蝶优化算法的光伏MPPT方法[J].计算机仿真，2023，40（12）：108-112.

[9]聂宏新，冯传奋，任帅.基于PSO-LSTM优化模型的网络流量预测研究[J].电信工程技术与标准化，2023，36（10）：18-21.

[10]陈皓.基于小波神经网络的移动网络流量预测研究[J].电子世界，2020（15）：81-82.

【通联编辑：谢媛媛】