基于改进蛇优化算法的永磁同步电机电气参数辨识

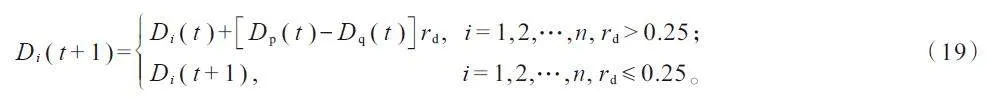
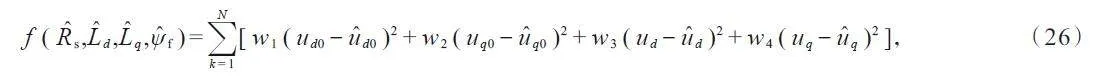
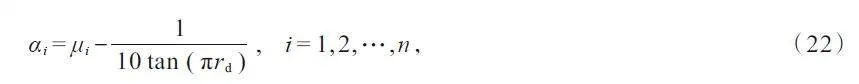
摘要：空间天线驱动单元控制器的精确设计依赖于永磁同步电机电气参数的准确获取，高精度的电气参数辨识是电机参数可靠获取的基础。针对标准蛇优化算法在永磁同步电机电气参数辨识时存在的收敛速度较慢、辨识精度不高、易陷入局部最优等缺点，引入Tent 混沌映射与准反向学习策略增强初始蛇群多样性，改进食物量与环境温度阈值提高算法收敛速度，利用柯西变异布谷鸟搜索算法提升算法全局优化搜索能力及鲁棒性，形成了一种改进蛇优化算法。利用提出的改进蛇优化算法，对某空间天线驱动单元中的永磁同步电机进行电气参数辨识。结果表明，相较于标准蛇优化算法，改进蛇优化算法具有更高的辨识精度、更快的收敛速度和更好的鲁棒性。

关键词：永磁同步电机；蛇优化算法；参数辨识；Tent 混沌映射；柯西变异布谷鸟算法

中图分类号：TM351 文献标志码：A 文章编号：1000-582X（2024）11-081-13

永磁同步电机（permanent magnet synchronous motor，PMSM）具有体积小、功率密度高和运行稳定等特点，在航空航天、机床和机器人等高技术领域得到广泛应用[1]。航天领域中，高精度空间天线的驱动单元（电机与谐波减速器系统）已越来越多采用永磁同步电机作为动力源，电机在低转速下驱动减速器以极低的转速控制天线的在轨姿态调整。低转速运行时，永磁同步电机处于高非线性、大脉动的复杂动态响应工作区，电机的动态机械特性较差，控制难度较大。为了实现对电机高动态响应、高精度与低扰动控制，以达到对驱动单元的高性能控制，采用电流环、速度环和位置环三闭环矢量控制策略。控制系统中，控制参数的正确设计依赖于精确的电机电气参数，但是在实际情况下，受温度、负载扰动、磁通饱和空间环境等诸多因素影响，电机电气参数偏离设计值，导致控制器设计参数与电机电气参数失配，电机控制性能严重偏离理论设计结果[2⁃3]。精确的电气参数获取技术与方法的构建，已成为实现PMSM，尤其是航天级低转速PMSM高性能控制的重要工作。

PMSM 动态电气参数的获取通常采用参数辨识的方法，较为常见的参数辨识方法有数值算法和人工智能算法等两大类[4]。数值算法中较为典型的有最小二乘法[5-6]、卡尔曼滤波法[7-8]和模型参考自适应法[9]等。因受限于数值算法本身的特点，大多数方法都存在辨识精度不高、计算量大、算法设计复杂、辨识参数较少等缺陷。例如，Yu 等[5]采用递推最小二乘法辨识了基于αβ 坐标系描述的PMSM 参数，以较快的收敛速度获得了较高精度的辨识参数，但算法存在计算量大与数据饱和影响参数辨识结果的缺陷。石建飞等[6]提出了基于折息递推最小二乘法的PMSM参数辨识算法，通过引入遗忘因子和加权因子，克服了传统最小二乘法中收敛速度慢与数据饱和对辨识精度影响的缺点。但是，算法存在设计较为复杂、计算量大和辨识精度不高的问题。李垣江等[9]提出了基于模型参考自适应的分步PMSM参数辨识方法，该方法收敛速度较快，但是辨识精度依赖于自适应律设计的合理性。

基于数值算法的固然缺陷，针对PMSM参数辨识中所表现出的非线性、强耦合和多变量特性，研究人员开展了大量人工智能算法在参数辨识方面的研究和探索[10-14]。谷鑫等[10]利用人工神经网络对PMSM 进行了电机参数辨识，以最小均方权值作为收敛策略，实现了电机参数的较高精度辨识，但该方法的辨识精度有赖于最小均方权值中的收敛因子选取。肖曦等[11]利用遗传算法对内埋式永磁同步电机进行了参数辨识，采用帕德逼近法对d 轴和q 轴电流方程进行离散化处理，通过建立待辨识电机参数与遗传算法辨识参数的对应关系，逆向递推实现了电机参数的高精度辨识，但是该方法计算处理过程较为复杂。Jin 等[12]针对表贴式永磁同步电机提出基于灰狼与郊狼优化算法的混合优化算法进行电机参数辨识，通过在适应度函数中设置永磁体磁链惩罚项，提高了优化算法对永磁体磁链辨识精度，但混合算法的计算量大量增加。吴定会等[13]针对PMSM多参数辨识问题，提出了一种基于高斯和柯西变异的珊瑚礁算法，实现了定子电阻、dq 轴电感、永磁体磁链等电气参数的同时辨识，具有较好的收敛精度，但是计算量较大且收敛速度较慢。Wu 等[14]将云隶属度模糊推理和自适应变步长的Lévy 飞行策略嵌入布谷鸟算法，并将算法应用于PMSM 的参数辨识，该方法虽然相对于标准布谷鸟算法的全局优化搜索能力得到了提升，但迭代后期的收敛速度较慢。

综上，与数值算法相比，高性能的智能算法在PMSM电气参数辨识方面的优势更为明显。笔者针对某空间天线驱动单元中的低速PMSM 高性能控制技术需求，基于标准蛇优化算法（snake optimization algorithm，SOA）[15]较强的鲁棒性和全局优化搜索能力，提出一种全局优化搜索能力更强的改进蛇优化算法（improvedsnake optimization algorithm，ISOA），并利用改进算法进行电机电气参数辨识。改进策略有：1）引入Tent 混沌映射与准反向学习策略增强初始蛇群多样性；2）改进食物量与环境温度阈值提高算法收敛速度；3）利用柯西变异布谷鸟算法提升算法全局优化搜索能力及鲁棒性。ISOA 高精度地辨识了PMSM 的定子电阻、dq 轴电感和永磁体磁链等电气参数，且收敛速度快、鲁棒性较好，为PMSM电气参数高精度辨识提供了一种借鉴思路和技术途径。

1 永磁同步电机数学模型及电气参数辨识模型

1.1 永磁同步电机数学模型

PMSM是一个非线性、强耦合和多变量的复杂系统，若忽略铁芯损耗与涡流损耗等干扰因素，在dq 轴同步旋转坐标系下其电压方程[3]可表示为

式中，带“ˆ”的参数为相应参数的辨识计算结果。

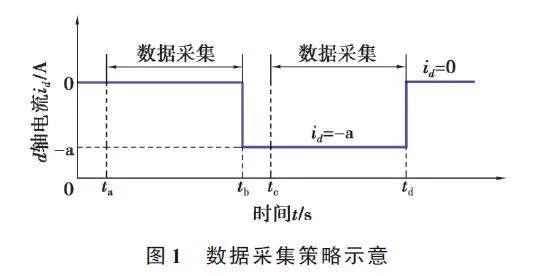
电气参数辨识时，数据采集策略如图1 所示。图中纵坐标“-a”为注入的负序直轴电流。对id = 0 和id ≠ 0 这2 种控制策略进行数据采集，对应的采集时间区间分别为[ta ， tb]和[tc ， td]，为了防止采集到电机不稳定状态数据，在2种控制策略切换后设置采样延时Δt = tc - tb。

2 标准蛇优化算法

SOA 是由Hashim 等[15]于2022 年提出的优化算法，该算法的灵感源于蛇群的觅食和交配行为，这2 种行为主要受食物量和环境温度影响。该算法将蛇群分为个体数量相等的雄性蛇群和雌性蛇群，假设蛇群个体总数为Np，则雄性蛇群和雌性蛇群个体数分别为Nm = Nf =Np/2。算法主要分为全局探索和局部开发2 个阶段。

2.1 全局探索阶段

假设求解空间为蛇群觅食空间，定义空间内的食物量为

式中：fb，m 和fb，f分别为雄性蛇群和雌性蛇群的最优适应度值；Xb，m 和Xb，f分别为雄性蛇群和雌性蛇群当前所处的最优位置。

3 改进蛇优化算法

SOA 是一种具有较强优化能力的算法，但其在局部开发阶段易陷入局部最优解，即出现全局优化搜索能力不足。因此，为了更好地平衡算法的全局探索能力与局部开发能力、加快算法收敛速度并增强其鲁棒性，提出以下改进策略。

3.1 蛇优化算法改进策略

3.1.1 基于Tent 混沌映射与准反向学习策略的蛇群位置初始化

种群初始位置的多样性对于蛇优化算法求取全局最优解起着重要的作用。混沌运动具有随机性、遍历性、规律性和对初值敏感等特点，有助于增强智能算法跳出局部最优解，进而获得较好的全局优化搜索能力[16]。混沌映射中，Tent 混沌映射在[0， 1]生成的随机数较为均匀，可以较好地增强蛇优化算法的种群初始位置多样性[17]。因此，文中引入Tent 混沌映射进行蛇群位置初始化。

基于Tent 混沌映射的混沌序列为[16]

式中：zi为混沌序列的第i 个混沌值，zi∈[0， 1]；ε 为控制参数，ε∈（0， 1），参考文献[18-19]，并结合仿真实验结果，文中取ε = 0.6。

根据式（13），可得出基于Tent 混沌映射的蛇群个体初始位置为

Xi = b0 + zi （ b1 - b0 ） ， i = 1，2，…，Np。（14）

为了进一步提高蛇群初始位置的多样性，引入准反向学习策略[1]。基于准反向学习策略的基本原理，若存在一点x（x∈[c1， c2]，其中c1、c2分别为x 取值区间的最小值和最大值），则其准反向点x*定义为[1]

由公式（15）可知，x*为区间[（c1+c2）/2， c1+c2-x]内的均匀分布随机数。将Tent 混沌映射与准反向学习策略联合使用，形成Tent 混沌映射-准反向学习策略。根据式（14）和（15），可得基于Tent 混沌映射-准反向学习策略的蛇群中个体初始位置为

式中：Pi为第i 个蛇的初始位置；pr为蛇群准反向学习概率，文中取pr = 0.3[1]。

蛇群位置初始化时，将基于Tent 混沌映射的蛇群初始位置X 与Tent 混沌映射-准反向学习策略产生的蛇群初始位置P 混合，形成混合的蛇群初始位置Xc = {X∪P}。根据适应度值大小，从Xc中选择Np个适应度值较好的位置作为蛇群初始位置。

3.1.2 食物量阈值与环境温度阈值的改进

在全局探索阶段和局部开发阶段，SOA 的收敛速度受食物量阈值和环境温度阈值的影响较大。根据式（7）和式（9），当最大迭代次数Nmax =200 时，食物量与环境温度随迭代次数的变化曲线如图2 所示。

由图2 可知，食物量与迭代次数呈正相关性。在不明显削弱标准蛇算法全局探索能力的前提下，为了减少其全局优化搜索迭代次数，加快算法的收敛速度，以电机电气参数辨识精度为目标，经多次试算和调整，最终将标准蛇优化算法中食物量阈值Th1 = 0.25 调整为Th1 = 0.22。环境温度与迭代次数呈负相关性。兼顾标准蛇算法在局部开发阶段的收敛速度与计算精度，采样同样的方法，将环境温度阈值由Th2 = 0.6 调整为Th2 = 0.8。

3.1.3 基于柯西变异的布谷鸟搜索算法

布谷鸟搜索算法（cuckoo search algorithm，CSA）由Yang 等[20]于2009 年提出，算法的灵感源于布谷鸟群搜索鸟巢孵蛋的行为。CSA 算法采用Lévy 飞行策略，具有较强的跳出局部最优解的能力。因此，引入CSA以提升标准SOA 跳出局部最优解、搜索全局最优解的能力。

基于布谷鸟群搜索鸟巢孵蛋的策略，若鸟群中个体数量为n，当鸟群搜索到新的鸟巢时，布谷鸟群个体的位置更新为[20]

Di （ t + 1 ）= Di （ t ）+ α （ Di （ t ） - Db ） L， i = 1，2，…，n， （17）

式中：α 为布谷鸟飞行的步长控制因子，α∈（0， 1）；Db为布谷鸟群当前所处的最优位置；L 为服从Lévy 分布的随机搜索路径，计算公式为[21-22]

L =u/| v |1/1.5 ， （18）

式中，u 和v 均为正态分布函数，分别服从N（0， 0.696 6）和N（0， 1）。

布谷鸟除在自己所筑的鸟巢中孵蛋外，还会借用其他鸟巢孵蛋，其被宿主发现的概率为0.25[21]。此时，布谷鸟群中个体的位置更新为

式中，Dp（t）和Dq（t）表示第t 次迭代时布谷鸟群中除个体i 之外的任意两只鸟的位置。

在CSA 中，步长控制因子α 用于控制算法的搜索区域，较大的α 取值有利于全局探索，较小取值则有利于局部开发，在实际应用时通常取α = 1，这导致计算中难以较好地平衡全局探索能力和局部开发能力。基于此，引入柯西变异优化α，使每只布谷鸟获得不同的飞行步长控制因子[21]，从而促进算法的全局优化搜索能力。

柯西变异源于柯西分布，其累积分布函数为[23]

式中：ξ 为柯西分布的随机变量；μ 为位置参数。

对于式（20），若令F（ξ） = rd，可得随机变量ξ 为

为了提高布谷鸟搜索算法的适应性，将柯西分布中的随机变量ξ 作为步长控制因子α。因此，任意布谷鸟的飞行步长控制因子可以表示为

式中，μi为第i 只布谷鸟的位置参数，其计算公式为

μi = 0.1μi - 1 + 0.9LS ， i = 1， 2， …， n， （23）

式中，LS为Lehmer 平均值，计算方法见文献[24]。式（23）为一递推表达式，位置参数μi的初值取μ0 = 0.5。

通过求解式（17）～（19）、（22）和（23），即可以实现标准SOA 的柯西变异布谷鸟搜索改进。当搜索策略为布谷鸟群搜索到自己的鸟巢或在其他鸟巢孵蛋且未被宿主发现时，蛇群中雄性个体的位置更新为

Xi ，m （ t + 1 ）= Xi，m （ t ）+ αi，m （ Xi，m （ t ）- Xb，m ） Li，m， （24）

式中：αi，m 为蛇群中雄性个体的柯西变异布谷鸟飞行步长控制因子；Li，m 为蛇群中雄性个体的Lévy 随机搜索路径。

否则，雄性个体的位置更新为

Xi ，m （ t + 1 ）= Xi，m （ t ）+ （ Xp，m （ t ）- Xq，m （ t ）） rd， （25）

式中，Xp，m和Xq，m为柯西变异布谷鸟搜索时雄性蛇群中除个体i 之外的任意两蛇的位置。

蛇群中雌性个体的位置更新方式与雄性个体相同，也可以表示为类似式（24）和（25）的形式，因而不再赘述。

3.2 改进蛇优化算法的计算流程

在标准SOA 中引入Tent 混沌映射与准反向学习策略增强初始蛇群多样性，通过改进食物量与环境温度阈值提高算法收敛速度，利用柯西变异布谷鸟算法提升算法全局优化搜索能力及鲁棒性，形成了ISOA，其计算流程如图3 所示。图中的适应度值是由适应度函数计算获得的，适应度函数的构建与具体分析的问题有关，文中PMSM电气参数辨识的适应度函数为公式（26）（见4.1 节）。

4 基于改进蛇优化算法的永磁同步电机电气参数辨识

4.1 永磁同步电机电气参数辨识原理

采用ISOA 对PMSM电气参数进行辨识的过程，就是根据电机实际系统的dq 轴电压（ud和uq）与理论模型计算的dq 轴电压（û d 和û q）之差值，借助适应度函数f （R ̂s ，L ̂d ，L ̂q ，ψ̂ f ），利用ISOA 对理论模型中的待辨识参数（R ̂s、L ̂d、L ̂q、ψ̂ f）不断修正，从而得到PMSM电气参数的过程，电气参数辨识的原理如图4 所示。

以电机实际系统的dq 轴电流和转子电角速度ωe作为理论模型的输入参数，理论模型输出的dq 轴电压与实际系统的电压接近程度通过适应度函数进行评估，ISOA 根据评估结果对电机待辨识参数进行修正，修正后的电机参数作为理论模型中下一次迭代的模型参数。重复上述计算过程，直到适应度函数最小或执行完设定的最大迭代次数，即得到电机参数的辨识值。

mMNHHEG/3WsfDSzk5UAAWw==

由方程组（6）可知，PMSM 中dq 轴电压可以作为评价电气参数辨识精度的参数，因此，建立算法的适应度函数为

式中：N 为计算中输入的信号样本数量；w1、w2、w3和w4为权重系数，取值区间为（0， 1），且满足Σi = 14wi = 1。考虑到适应度函数中4 个权重系数对应的电压分量对于待辨识电气参数的辨识精度具有同等的重要性，因此，文中分析中4 个权重系数均取值为0.25[13]。

4.2 改进蛇优化算法的永磁同步电机电气参数辨识步骤

根据4.1 的电气参数辨识原理，结合ISOA 计算流程（见图3），形成电机电气参数辨识算法。

步骤1：在id = 0 和id < 0 这2 种控制策略下采集PMSM 的dq 轴电压（ud 和uq）、dq 轴电流（id 和iq）和电角速度ωe。

步骤2：设置蛇群个体总数、算法求解维度、求解区间和最大迭代次数；采用Tent 混沌映射-准反向学习策略（式（13）、（14）和（16）），初始化蛇群中个体的位置并计算初始适应度值（式（26））；进行蛇-群-雌-雄分类；定义蛇群食物量阈值与环境温度阈值。

步骤3：利用标准SOA（式（8）、式（10）～（12）、式（26）），更新蛇群中雌/雄性个体位置和对应的适应度值，确定蛇群最优适应度值及对应的位置；取上次迭代和本次计算的蛇群最优适应度值之小者作为蛇群当前最优适应度值，对应位置为蛇群最优位置。

步骤4：采用柯西变异布谷鸟搜索算法进一步更新SOA 获得的雌/雄性个体位置和对应的适应度值，再次计算蛇群最优适应度值及对应的位置；最优适应度值计算方法与SOA 相同。

步骤5：比较步骤3 和步骤4 获得的蛇群最优适应度值，以两者之小值作为本次循环的蛇群最优适应度值，对应位置为蛇群最优位置。

步骤6：判断算法是否达到最大迭代次数，若满足，则执行步骤7；否则返回步骤3。

步骤7：达到最大迭代次数后，输出蛇群的最优位置，即全局最优辨识参数，以及对应的适应度值，计算结束。

5 仿真实验

5.1 仿真分析模型

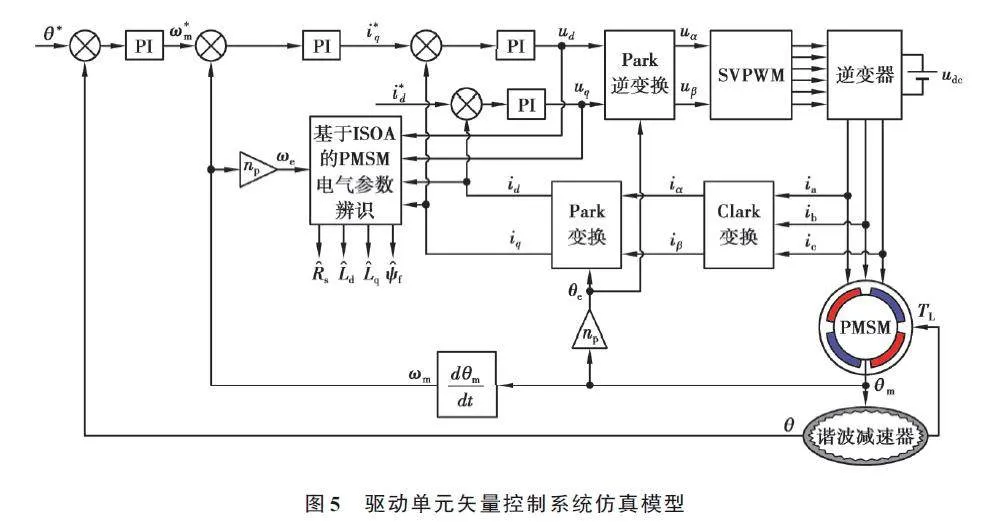
以某空间天线驱动单元为仿真分析对象，其由PMSM和谐波减速器组成，采用位置环、速度环和电流环三闭环的矢量控制策略，基于ISOA 原理建立的Matlab/Simulink 电气参数辨识仿真分析模型如图5 所示。

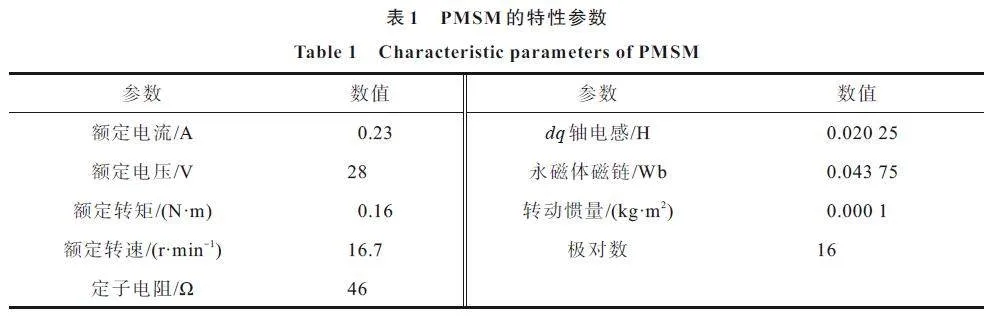
图5 中，PMSM 为航天级电机，特性参数如表1 所示；谐波减速器的传动比为100；负载等效转动惯量为1.07 kg·m2；电机转速为10 r/min；ia、ib、ic分别为电机的三相电流；iα、iβ分别为两相静止坐标系下的电流；i*d、i*q 分别为d 轴、q 轴参考电流；np为电机的极对数；θm为电机的机械角度；θe为电机电角度；ωm为电机的机械角速度；ω *m 为电机参考机械角速度；θ 为谐波减速器输出角度；θ*为谐波减速器参考角度；TL为谐波减速器反馈给电机的负载转矩；udc 为逆变器的直流母线电压；uα 和uβ 分别为α 轴、β 轴的电压。仿真实验环境为Intel（R） Core（TM） i5-10400F 型6 核CPU 与16 GB 运行内存的组合。

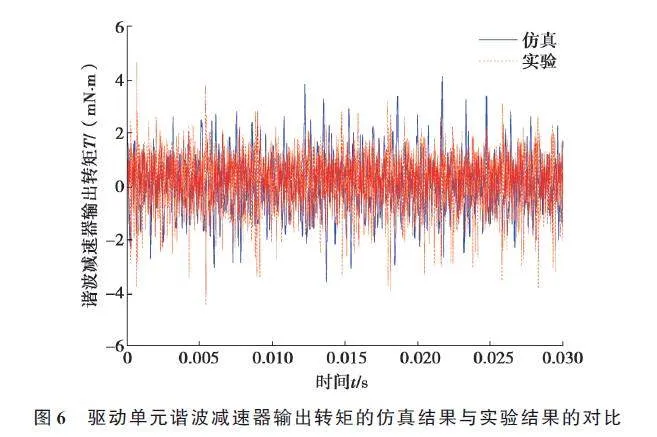
采用ISOA 对驱动单元中的PMSM 电气参数进行辨识时，算法的输入信号来自于驱动单元矢量控制系统的仿真结果，可靠的仿真结果取决于仿真模型的正确性。文中采用对比驱动单元稳定工作时谐波减速器输出转矩的实验结果与仿真结果的方法验证仿真分析模型的正确性。图6 为驱动单元中谐波减速器输出转矩的仿真结果与实验结果的对比。

从图6 中可以看出，由于仿真系统与电机硬件系统的差异性，加之实验的测试误差，导致谐波减速器输出转矩的仿真分析结果与实验结果存在一定的误差，两者的最大误差仅10.8%，可认为仿真分析结果与实验结果具有一致性，在一定程度上证明了文中建立的仿真分析模型各控制环节与实际的电机控制系统是吻合的，仿真分析模型正确。

5.2 仿真实验方案

构造辨识方程组（6）时，需要在驱动单元稳态运行阶段注入负序直轴电流，为避免注入电流过大而引起电机转速发生较大变化，同时不超过电机允许的弱磁范围[10， 25]，选取负序直轴电流id = −0.1 A，作用时间600 ms。待驱动单元运行稳定后，采用图1 所示的数据采集方法，采集id = 0 和id = -0.1 A 这2 种控制策略下的信息数据（id、iq、ud、uq、ωe），取采样周期Ts = 0.4 ms，采样数据量为1 000 组。采集的数据经低通滤波器滤波后存入Matlab 工作区，作为PMSM电气参数辨识算法的输入样本。

为了评价ISOA 9aQA1jEH5pZEdwL28wGYXw==对PMSM 电气参数的辨识性能与有效性，引入灰狼优化算法（grey wolf optimization，GWO）[26]，对GWO、标准SOA 与ISOA 的辨识结果进行了对比。为了消除参数配置差异可能引起的计算误差，3 种算法辨识时采用了相同的参数配置，如表2 所示。PMSM 的定子电阻和永磁体磁链等电气参数受工作环境影响一般不会超过设计值的40%[27]，设置相关参数时充分考虑了这一情况而使其充分远离实际值，以保证参数配置的合理性。算法中其余参数选择时，参考了文献[3， 15， 18， 21-23]研究成果，并经多次辨识试算调整确定。此外，为了排除算法单次运行的偶然性，分别对3 种算法各进行了30 次独立运行，将辨识参数和适应度值的平均值作为最终的辨识结果。

5.3 仿真实验结果与分析

图7 给出了PMSM转速为10 r/min 条件下，GWO、标准SOA 和ISOA 的电气参数辨识结果对比，表3 给出了3 种辨识方法的辨识性能对比。

由图7 可知，GWO、标准SOA 和ISOA 均使得电机定子电阻Rs、d 轴电感Ld、q 轴电感Lq和永磁体磁链ψf 4个辨识参数收敛到真实值附近，但是辨识的性能不同。与GWO 和标准SOA 相比，ISOA 的收敛速度更快，辨识精度更高，而且收敛过程的鲁棒性更好，如图7（b）～（e）。对于3 种算法在辨识性能上的差异性还可以从平均适应度值的收敛曲线看出（图7（a）），GWO 和SOA 的平均适应度值收敛过程较慢，且稳定值大于ISOA，或者说ISOA 的稳定平均适应度值更加趋近于0，即适应度值更优，ISOA 的全局优化搜索能力更强。

从图7（f）中可看出，ISOA 的计算时间明显大于SOA，但是小于GWO，完成电机参数辨识GWO、ISOA 和SOA 的计算时间分别为142.710、95.591、25.591 s（见表3），ISOA 的计算量约为SOA 的3.7 倍，但ISOA 显著提升了参数的辨识精度。

从表3 中可以看出，相较于GWO 和标准SOA，ISOA 的电气参数辨识误差非常小，误差最大的参数是d轴电感Ld，其误差为0.86%，表明改进算法的辨识是比较准确的，对于诸如文中分析的航天级电机等高精度控制环境已有足够的精度。

6 结 论

针对标准SOA 在辨识PMSM 电气参数时存在收敛速度较慢、辨识精度不高和易陷入局部最优解等缺点，提出了一种ISOA，并将其应用于PMSM 电气参数的多参数辨识。在ISOA 中引入Tent 混沌映射与准反向学习策略增强初始蛇群多样性，通过改进食物量与环境温度阈值提高算法收敛速度，利用柯西变异布谷鸟算法提升算法全局优化搜索能力及鲁棒性。基于某空间天线的驱动单元，在Matlab/Simulink 软件中仿真分析了GWO、SOA 和ISOA 这3 种算法对于PMSM 电气参数多参数辨识的性能，结果表明，ISOA 辨识性能较好，具有更高的辨识精度、更快的收敛速度和更强的鲁棒性。

通过建立ISOA 辨识算法获得永磁同步电机电气参数的高精度辨识，引入多个其他优化算法以提升算法辨识性能，但增加了ISOA 算法的计算量，提升算法辨识精度的同时兼顾合理的计算量是后续研究中非常有意义的工作。

参考文献

［ 1 ］ Ahandani M A， Abbasfam J， Kharrati H. Parameter identification of permanent magnet synchronous motors using quasiopposition-based particle swarm optimization and hybrid chaotic particle swarm optimization algorithms[J]. AppliedIntelligence， 2022， 52（11）： 13082-13096.

［ 2 ］ 吴春， 赵宇纬， 孙明轩. 采用测量电压的永磁同步电机多参数在线辨识[J]. 中国电机工程学报， 2020， 40（13）： 4329-4340.

Wu C， Zhao Y W， Sun M X. Multiparameter online identification for permanent magnet synchronous machines using voltagemeasurements[J]. Proceedings of the CSEE， 2020， 40（13）： 4329-4340. （in Chinese）

［ 3 ］ 张铸， 张仕杰， 饶盛华， 等. 改进樽海鞘群算法的永磁同步电机多参数辨识[J]. 电机与控制学报， 2022， 26（8）： 139-146.

Zhang Z， Zhang S J， Rao S H， et al. Multi-parameter identification of permanent magnet synchronous motor based onimproved salp swarm algorithm[J]. Electric Machines and Control， 2022， 26（8）： 139-146. （in Chinese）

［ 4 ］ Rafaq M S， Jung J W. A comprehensive review of state-of-the-art parameter estimation techniques for permanent magnetsynchronous motors in wide speed range[J]. IEEE Transactions on Industrial Informatics， 2019， 16（7）： 4747-4758.

［ 5 ］ Yu Y L， Huang X Y， Li Z K， et al. Full parameter estimation for permanent magnet synchronous motors[J]. IEEE Transactionson Industrial Electronics， 2022， 69（5）： 4376-4386.

［ 6 ］ 石建飞， 戈宝军， 吕艳玲， 等. 永磁同步电机在线参数辨识方法研究[J]. 电机与控制学报， 2018， 22（3）： 17-24.

Shi J F， Ge B J， Lü Y L， et al. Research of parameter identification of permanent magnet synchronous motor on line[J]. ElectricMachines and Control， 2018， 22（3）： 17-24. （in Chinese）

［ 7 ］ Wang Z W， Liu X， Wang W Z， et al. UKF-based parameter estimation and identification for permanent magnet synchronousmotor[J]. Frontiers in Energy Research， 2022， 10： 855649.

［ 8 ］ Li X， Kennel R. General formulation of Kalman-filter-based online parameter identification methods for VSI-fed PMSM[J].IEEE Transactions on Industrial Electronics， 2021， 68（4）： 2856-2864.

［ 9 ］ 李垣江， 董鑫， 魏海峰， 等. 基于改进模型参考自适应系统的永磁同步电机参数辨识[J]. 控制理论与应用， 2020， 37（9）：1983-1988.

Li Y J， Dong X， Wei H F， et al. Parameter identification method of permanent magnet synchronous motor based on improvedmodel reference adaptive system[J]. Control Theory & Applications， 2020， 37（9）： 1983-1988. （in Chinese）

［10］ 谷鑫， 胡升， 史婷娜， 等. 基于神经网络的永磁同步电机多参数解耦在线辨识[J]. 电工技术学报， 2015， 30（6）： 114-121.

Gu X， Hu S， Shi T N， et al. Muti-parameter decoupling online identification of permanent magnet synchronous motor based onneural network[J]. Transactions of China Electrotechnical Society， 2015， 30（6）： 114-121. （in Chinese）

［11］ 肖曦， 许青松， 王雅婷， 等. 基于遗传算法的内埋式永磁同步电机参数辨识方法[J]. 电工技术学报， 2014， 29（3）： 21-26.

Xiao X， Xu Q S， WANG Y T， et al. Parameter identification of interior permanent magnet synchronous motors based on geneticalgorithm[J]. Transactions of China Electrotechnical Society， 2014， 29（3）： 21-26. （in Chinese）

［12］ Jin Z， Sun X， Lei G， et al. Sliding mode direct torque control of SPMSMs based on a hybrid wolf optimization algorithm[J].IEEE Transactions on Industrial Electronics， 2021， 69（5）： 4534-4544.

［13］ 吴定会， 黄旭， 全亚威， 等. 基于变异珊瑚礁算法的永磁同步电机参数辨识[J]. 系统仿真学报， 2018， 30（8）： 3024-3032.

Wu D H， Huang X， Quan Y W， et al. Parameter identification of permanent magnet synchronous motor based on mutation coralreef algorithm[J]. Journal of System Simulation， 2018， 30（8）： 3024-3032. （in Chinese）

［14］ Wu Z Q， Du C Q. The parameter identification of PMSM based on improved cuckoo algorithm[J]. Neural Processing Letters，2019， 50（3）： 2701-2715.

［15］ Hashim F A， Hussien A G. Snake Optimizer： a novel meta-heuristic optimization algorithm[J]. Knowledge-Based Systems，2022， 242： 108320.

［16］ 滕志军， 吕金玲， 郭力文， 等. 一种基于Tent 映射的混合灰狼优化的改进算法[J]. 哈尔滨工业大学学报， 2018， 50（11）：40-49.

Teng Z J， Lü J L， Guo L W， et al. An improved hybrid grey wolf optimization algorithm based on Tent mapping[J]. Journal ofHarbin Institute of Technology， 2018， 50（11）： 40-49. （in Chinese）

［17］ 李雪岩， 李雪梅， 李学伟， 等. 基于混沌映射的元胞遗传算法[J]. 模式识别与人工智能， 2015， 28（1）： 42-49.

Li X Y， Li X M， Li X W， et al. Cellular genetic algorithm based on chaotic map[J]. Pattern Recognition and ArtificialIntelligence， 2015， 28（1）： 42-49. （in Chinese）

［18］ Yu Y， Gao S C， Cheng S， et al. CBSO： a memetic brain storm optimization with chaotic local search[J]. Memetic Computing，2018， 10（4）： 353-367.

［19］ 周鹏， 董朝轶， 陈晓艳， 等. 基于阶梯式Tent 混沌和模拟退火的樽海鞘群算法[J]. 电子学报， 2021， 49（9）： 1724-1735.

Zhou P， Dong C Y， Chen X Y， et al. A salp swarm algorithm based on stepped tent chaos and simulated annealing[J]. ActaElectronica Sinica， 2021， 49（9）： 1724-1735. （in Chinese）

［20］ Yang X S， Deb S. Cuckoo search via Lévy flights[C]// 2009 World Congress on Nature & Biologically Inspired Computing.Piscataway： IEEE， 2009： 210-214.

［21］ Cheng J T， Xiong Y. Multi-strategy adaptive cuckoo search algorithm for numerical optimization[J]. Artificial IntelligenceReview， 2023， 56（3）： 2031-2055.

［22］ 邢致恺， 贾鹤鸣， 宋文龙. 基于莱维飞行樽海鞘群优化算法的多阈值图像分割[J]. 自动化学报， 2021， 47（2）： 363-377.

Xing Z K， Jia H M， Song W L. Levy flight trajectory-based salp swarm algorithm for multilevel thresholding imagesegmentation[J]. Acta Automatica Sinica， 2021， 47（2）： 363-377. （in Chinese）

［23］ 刘航， 张晓明， 汪长剑. 基于柯西分布和父种轮换机制的种子优化算法[J]. 模式识别与人工智能， 2021， 34（7）： 581-591.

Liu H， Zhang X M， Wang C J. Bean optimization algorithm based on cauchy distribution and parent rotation mechanism[J].Pattern Recognition and Artificial Intelligence， 2021， 34（7）： 581-591. （in Chinese）

［24］ Høibakk R， Lukkassen D， Meidell A， et al. Geometric construction of some lehmer means[J]. Mathematics， 2018， 6（11）：251-268.

［25］ 刘细平， 胡卫平， 丁卫中， 等. 永磁同步电机多参数辨识方法研究[J]. 电工技术学报， 2020， 35（6）： 1198-1207.

Liu X P， Hu W P， Ding W Z， et al. Research on multi-parameter identification method of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society， 2020， 35（6）： 1198-1207. （in Chinese）

［26］ Mirjalili S， Mirjalili S M， Lewis A. Grey wolf optimizer[J]. Advances in Engineering Software， 2014， 69（3）： 46-61.

［27］ Ramakrishnan R， Islam R， Islam M， et al. Real time estimation of parameters for controlling and monitoring permanent magnetsynchronous motors[C]// IEEE International Electric Machines & Drives Conference. Piscataway： IEEE， 2009： 1194-1199.

（编辑 詹燕平）