基于动力学模型的智能阀门控制优化策略

摘 要：为了提高智能阀门阀位控制的精确度，避免出现超调和阀位震荡等问题，本研究介绍了智能阀门定位装置的结构和工作原理，在此基础上，针对气动执行机构建立了受力方程，并根据阀杆的受力特点提出相应的牛顿运动方程，进而形成阀位气动控制动力学模型。该模型显示，阀杆受到的摩擦力、气动执行机构的进气量或者出气量为不稳定因素，其中存在未知参数。根据动力学模型对阀位运行的关键参数进行整定，包括行程类型、阀杆最大运动速度及其过冲量、阀杆基准运行速度及对应的PWM信号量、最小启动PWM信号，利用整定后的参数改进传统的阀门五步开关控制算法，制定优化的控制策略。

关键词：智能阀门；阀位气动控制；动力学建模

中图分类号：TH 134 " " " " 文献标志码：A

智能阀门设计了气动执行机构，将气源产生的推力作用于阀杆，进而控制阀位移动量及阀门开度。由于气动过程较为复杂，受到很多因素的影响，因此在实际应用过程中有可能出现超调。为了解决该问题，研究其动力学过程有助于挖掘关键影响因素，并制定提高控制精度的策略。

1 智能阀门定位装置

1.1 智能阀门定位装置工作原理

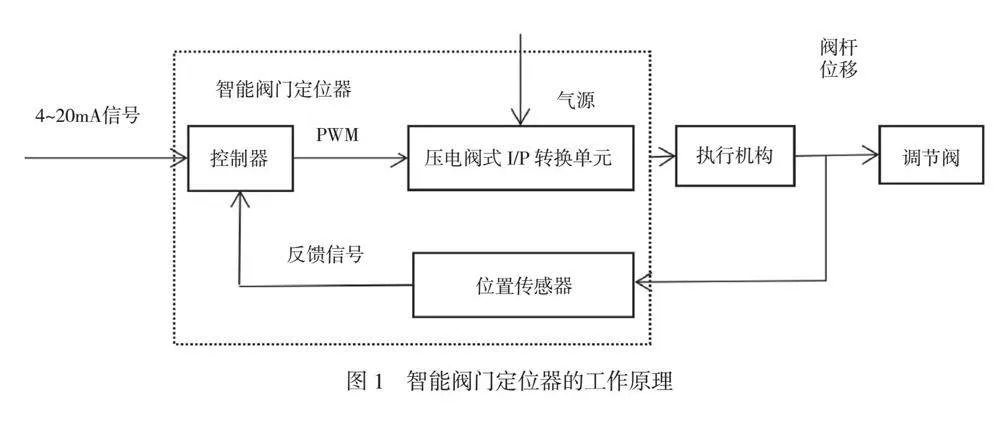
阀门定位器是智能阀门的定位装置，能够根据设定的信号改变阀杆的运动幅度，进而实现阀门开度控制，其工作原理如图1所示。由系统设定阀门开度的电信号，其电流强度通常在4 mA～20 mA，阀门的实际开度取决于阀杆的位移量。智能阀门定位器由控制器、压电阀式I/P转换单元和位置传感器组成，能够将电信号作用于执行机构，进而控制调节阀。

1.2 智能阀门定位装置的主要组件及功能

1.2.1 压电阀式I/P转换单元

智能阀门定位器的控制器在接收电信号后，以脉冲宽度调制（Pulse Width Modulation，PWM）的方式将信号传输至压电阀式I/P转换单元，再由该转换单元将PWM信号转变为气动信号，执行机构受到气动信号的驱动，作用于阀杆，进而控制调节阀[1]。压电阀的工作原理为逆压电效应，在本研究中，压电阀的型号为HOERBIGER-P20，其技术指标见表1。

1.2.2 气动执行机构

智能调节阀采用气动薄膜式执行机构，将高压气源作为动力能源，压电阀式I/P转换单元向执行机构发出压力信号，其信号量为2 kPa～10 kPa，通过高压气源将信号转化为阀杆的推力。气源通入薄膜气室，产生特定大小的作用力，使弹簧发生形变，进而推动阀杆[2]。阀杆的动作量与信号的压力值成正比。

1.2.3 位移传感器

为了精确控制阀杆的位移量，在智能阀门定位器中集成有位移传感器，用于向控制器反馈阀杆的位置信息，本研究使用的位移传感器为霍尼韦尔HMC1501型。在实际应用过程中，必须检验位移传感器的准确性，如果不合格，就应对其进行调试，直至满足要求。具体的检测方法如下：使位移传感器自转一圈，在该过程中采集传感器的模拟信号量，再计算角度θ。如果-20°≤θ≤20°，就证明位移传感器精度合格[3]。

1.2.4 附件

除了以上组件外，在智能阀门控制系统中还存在放大器、减压阀等附件，前者的作用是根据气源压力和控制信号调节气体的流量，后者用于控制进气管道的压力。放大器的工作介质为空气，额定流量为600 L/min，输出压力在0.50 MPa～0.99 MPa。减压阀采用气体驱动方式，其压力为0.05 MPa～0.70 MPa。

2 智能阀门阀位气动控制动力学建模

2.1 气动执行机构受力方程建模

智能阀门的气动控制装置通过气动执行机构进行阀位控制，因此阀位气动控制动力学建模主要针对气动执行机构。从智能阀门定位装置的工作原理可知，执行机构动力学建模的影响因素包括压电阀的进气量和出气量、进气压力、气动推力以及阀杆受力等，最终的阀位是由阀杆的位移量决定的。当阀杆处于运动状态时，其动力学方程如公式（1）所示。

Ft（t）=FQ（t）-Fk-Ff（x）+Fm-Fr " " （1）

式中：Ft（t）为阀杆运动至时间t受到的合力；FQ（t）为气源在时间t的推力；Fk为复位弹簧的弹力；Ff（x）为阀杆的摩擦力；x为阀杆的位移量；Fm为阀杆及辅助组件的重力；Fr为流体的扰动作用力。当阀杆处于静止状态时，其受力关系如公式（2）所示。

FQ（t）=Fk-Ff0（x）+Fm-Fr=0 （2）

式中：Ff0（x）为阀杆的静摩擦力；参数Fk=K（x+x（）），其中，K为弹簧的弹性系数；当执行机构未进气时，复位弹簧的变形量为x0；Fm为质量和重力加速度的乘积。参数Fr的计算过程如公式（3）所示。

（3）

式中：P3、P4为阀芯两侧的压力；S为压力P3侧的作用面积；ds为阀杆截面积的直径；S-1/4d2s为压力P4侧的作用面积。

阀杆运动过程中的摩擦力计算过程如公式（4）所示。

Ff（x）=fcSgn（x'）+x'fv " " " "（4）

式中：x'为位移对时间的一阶微分，其物理意义为阀杆的运动速度；fc为恒定的摩擦力；Sgn（·）为阶跃函数；fv为与速度相关的黏性摩擦力。气源推力FQ（t）的计算方法为FQ（t）=AgP1（t），其中，将气缸中薄膜的有效受力面积记为Ag，P1（t）为气缸内气体的背压，气缸的进气量对P1（t）的大小具有显著的影响[4]。

2.2 动力学建模分析

阀杆的运动过程始终满足牛顿运动规律，根据其受力方程可得到阀杆的牛顿运动方程，如公式（5）所示。

mx\"=Ft（t）=FQ（t）-Fk-Sgn（x'）Ff（x）+Fm-Fr " （5）

式中：x''为阀杆位移对时间的二阶微分，其物理含义为阀杆的加速度。

从物理含义中可推导出mx''=mv'=ma，v为阀杆的运动速度。当阀门定位器采用压电式I/P转换单元时，由系统给定阀位控制信号，该信号经过微型控制器的处理，转变为PWM信号，通过不同的占空比来调节进气量，从而形成不同压力的高压气源，阀杆在高压气体的带动下实现运动，控制最终的阀位。阀门定位器的性能如公式（6）所示。

（6）

式中：x（t）代表阀门定位器的位置；u（t）代表输入信号，即控制阀的开度信号；Td代表定位器的时延；Kp代表定位器的增益；dx（t）代表阀门定位器位置关于时间的变化率。

从以上过程可知，阀杆的运动控制问题包括2个关键因素。1）终端位置固定。2）终端时间不固定，需要在这2个条件下进行控制。接收信号前，阀杆处于静止状态；接收信号后，阀杆从静止状态向运动状态过渡，此时需要克服最大静摩擦力，该过程需要满足以下条件，如公式（7）所示。

Ft（0）=FQ（0）-Fk-Ffmax（x0）+Fm-Frgt;0 " （7）

式中：Ffmax（x0）为阀杆的最大静摩擦力。如果阀杆的运动速度过快，就有可能造成气动系统震荡，为了避免该问题，必须适当限制阀杆的运动速度，将最大运动速度记为vmax，阀杆的实时运动速度v（t）和总运动时间t满足v（t）≤vmax，0≤t≤tf[5]。

2.3 调节阀特性参数整定问题

由以上分析可知，在阀门定位装置的动力学模型中存在部分不确定因素，包括流体扰动和摩擦力的跳变，其中涉及未知的参数，这些参数与阀杆的运动控制有关。如果根据工程经验整定运动方程中的未知参数，就会导致定位装置的通用性不足。另外，调节阀来自不同的生产厂家，其结构设计、工作特性存在一定的差异。即使定位器的型号相同，其安装方式、工作环境不同，工作时的气源压力不稳定，同样有可能影响阀杆的运动控制。针对这些问题，应该引入调节阀的特性参数，并对其进行整定。

3 基于动力学模型和参数整定的阀位最优控制策略

本次研究中，相关工作人员深入了解阀门系统动力学特性，引入参数整定法，建立数学模型，通过这种方式观察阀门在气动控制过程中的响应情，为制定有效的阀位控制策略提供理论基础。同时，研究人员采用最优控制策略，提高阀门控制系统稳定性、精确性以及响应速度，提高工业生产自动化水平。

3.1 五步开关控制算法的基本原理

3.1.1 基本原理分析

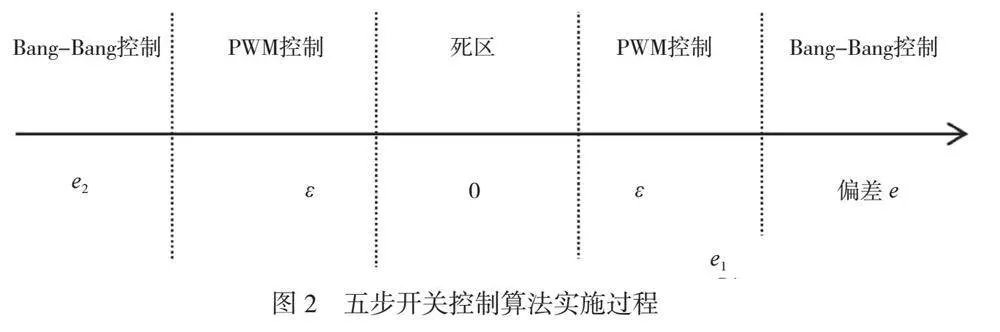
五步开关控制算法在调节阀控制中应用广泛，其实施过程如图2所示。由图2可知，该控制算法将脉冲宽度调制（Pulse Width Modulation，PWM）控制和起停式控制（Bang-Bang）相结合，在控制过程的初始阶段，由Bang-Bang控制发挥作用。此时，阀杆上受到的作用力最大，因此加速度也最大。然后以稳定的PWM信号控制阀杆，保持一定的阀位运动速度，当接近死区时取消控制，阀杆通过惯性达到设定的阀位。参数e2为排气阶段的阀位分界点，ε为死区范围的边界点，充气阶段的阀位分界点记为e1，阀位的最终误差记为e[6]。

3.1.2 控制过程

阀位调节是控制系统中的一个重要环节，需要经过三个阶段，三个阶段相互衔接，构成了高效调节系统。这种精密的控制过程可以在不同误差范围内，灵活、稳定地进行阀位调节。1）当e＞e1或者e＜e1时，说明阀位的反馈值和设定值存在显著的差异，此时电动阀的进气口或排气口受到阀门定位器的控制，进入全开状态，通过Bang-Bang控制实现排气或者进气，Bang-Bang控制模式的调节速度较快，能够快速缩小误差。2）当-e2≤e≤-ε或者ε≤e≤e1时，说明阀位的反馈值与设定值较为接近，此时，阀门定位装置通过PWM模式控制阀位，该方法能够根据现有情况合理输出PWM信号，进行小幅度阀位调节，以相对平缓的速度控制阀位的误差。3）当elt;ε时，说明阀位已进入死区，此时智能阀门定位器进入保持状态，电动阀将停止进气或者排气。

3.1.3 局限性分析

传统的五步开关控制算法在部分场景下有一定的局限性。例如，当阀位调节幅度较小时，该控制算法容易出现超调。另外，在控制过程中的各分界点缺少明确、量化的实现手段。对于不同类型的气动阀来说，由于结构、内部摩擦力等因素存在差异，因此传统的五步法调节模式缺乏足够的通用性。

3.2 阀门定位装置影响因素分析

门定位装置的性能受到多方面因素的影响，例如摩擦力、进气量或排气量、控制算法的质量以及环境条件的变化等。深入了解这些影响因素，有助于相关从业人员优化阀门定位装置设计，提高其在工业生产过程中的可靠性。

3.2.1 摩擦力

3.2.1.1 摩擦力对阀位运行距离的影响

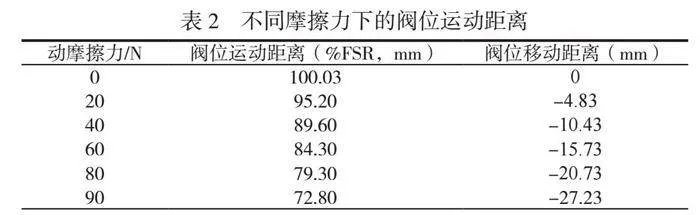
当阀杆运动时，先克服最大静摩擦力，再进入运动状态，在运动过程中还需克服动摩擦力。在不考虑静摩擦力的情况下，采用相同大小的气源压力，利用动力学模型分别计算阀位的运动距离，按照10 Hz的频率进行采样，结果见表2。理想状态是动摩擦力为0 N，阀位的额定行程为FSR，从数据可知，随着动摩擦力增加，阀位的最终行程持续下降。

3.2.1.2 选取调节阀填料

在调节阀中设置填料，其作用是填充阀盖和阀杆之间的空隙，使其达到良好的密封性，填料也会引起摩擦力差异。当前，常用的填料为聚四氟乙烯和石墨，聚四氟乙烯的摩擦力更小，使用聚四氟乙烯填料有利于提高对阀位的控制能力。

3.2.2 进气量或排气量

从动力学模型可知，进气量的大小影响了阀杆的受力，进而改变阀位的运动距离。本研究利用可调节进气量的辅助进气装置进行模拟，该装置由腔体、流量调节手轮、弹簧以及推杆等组成。将该装置作为调节阀的气源进行试验。将辅助进气装置的手轮开度分别设置为30%、40%、50%……100%，对比不同开度的阀位运行速度，以90%开度和100%开度为例，其对应的阀杆速度分别为0.8 m/s、0.2 m/s，说明开度越大，阀杆受力和运行速度越大。如果进气量不足，阀位就无法达到设定的位置；如果进气量过大，阀位就有可能出现超调。

3.3 参数整定方法

参数整定的内容包括4个方面，分别为最小启动PWM信号量、行程类型、阀杆最大运动速度及过冲量、阀杆基准运动速度及相应的PWM信号量。以阀杆最大运动速度及其过冲量整定为例，其整定流程如下：充气→判断是否达到最大阀位运行速度vup→如果未达到那么继续充气→如果达到那么保持3 s→计算充气阶段的过冲量→充气到顶端→排气→判断是否到达最小阀位运行速度vdown→如果未达到那么继续排气→如果达到那么保持3 s→计算排气阶段的过冲量→返回。例如，调节阀行程类型的整定流程如下：开始→下达Bang-Bang排气指令→判断气缸内气体是否排出→如果未排出那么继续排气→如果排出到位那么记录当前阀位反馈值→下达Bang-Bang进气指令→判断阀位是否变化→如果阀位增大，那么为反行程→如果阀位减少，那么为正行程。

3.4 最优控制策略

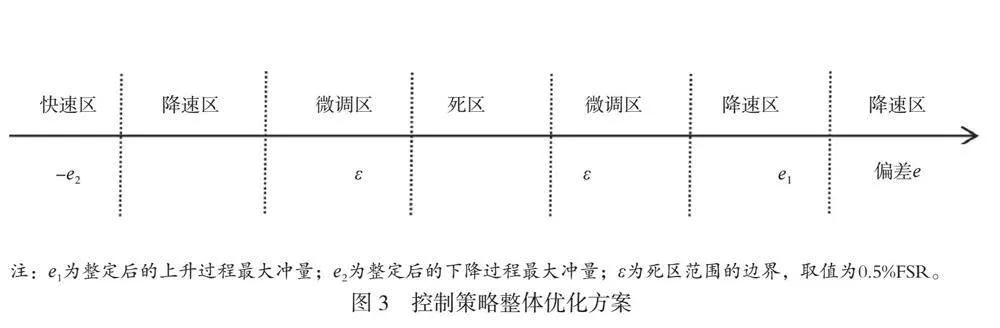
以五步开关控制算法为基础，引入降速区、微调区和快速区，优化后的控制策略如图3所示。控制过程采用的具体方法如下：1）在阀位调节过程启动后，阀杆先进入快速运动区，此时采用Bang-Bang控制模式。2）当偏差e的值在最大过冲量和最小过冲量之间时，阀位进入降速控制区，此时采用PWM控制模式。3）如果阀位实时运动速度v（t）小于整定后基准速度vmax，那么阀位进入微调区。在这种控制模式下，阀位的实时运动速度不会超过最大速度限值，避免了阀位震荡的问题，并且阀位将以相对平缓的速度进入死区。当阀位运行过程进入死区时，x（tf）-xset的绝对值不能大于偏差阈值，此时，压电阀进入保持状态，终止进气或者排气操作。

4 结语

综上所述，本研究针对智能阀门定位装置的气动执行机构建受力方程，并且根据牛顿运动定律提出阀杆的动力学方程，从动力学模型中发现影响阀门开度控制精度的关键因素，包括阀杆的基准速度、行程类型、阀位启动的最小PWM信号量、阀位最大运行速度及其过冲量、基准速度对应的PWM信号量等。以动力学模型为基础，对这些关键参数进行整定，再利用整定后的参数建立阀位的优化控制策略，有效地避免了超调、震荡等问题。

参考文献

[1]王怀康，赵立业.改进预估模糊PID控制在气动阀门定位系统中的应用[J].组合机床与自动化加工技术，2023（1）：156-157.

[2]丁琛.气动阀门控制方式在滤池控制系统中的比选应用[J].流体测量与控制，2023，4（3）：74-75.

[3]刘晶，李超然，张建楠，等.基于融合驱动的余热阀门控制优化方法[J].热力发电，2023，52（10）：298-299.

[4]李培金，黄超武，邹向阳.气动调节阀控制回路可靠性提升解决方案研究[J].仪器仪表用户，2023，30（9）：103-104.

[5]李海龙，李国镔，余道刚，等.某调节阀气动及振动噪声性能研究[J].热能动力工程，2023，38（10）：25-27.

[6]魏高鹏.气动调节阀气路控制原理分析[J].中国设备工程，2021（1）：169-170.