变步长微分控制的超声波换能器共振频率追踪

摘 要：超声波洁牙器在医疗领域，特别是口腔医学中成效卓越。然而，频率的突变和漂移对超声振动系统的稳定性和可靠性构成了挑战。本文针对医用口腔超声波洁牙器的工作特性，设计了一种新的谐振频率检测机制，并引入了一种基于最大电流法的变步长微分控制方法。结合相位锁定技术，笔者提出了一种复合控制方法，旨在提高超声波洁牙器的清洁效率和可靠性。模拟试验的结果验证了该方法的有效性和稳定性，表明新的频率追踪方法能在不同工作条件下精确追踪超声波换能器的频率，并具有较高的抗干扰能力。本研究为超声波设备的频率控制提供了新的思路，有望为超声波技术在口腔医疗中的应用提供更可靠和高效的支持。

关键词：超声波换能器；频率追踪；最大电流法；变步长算法；微分控制

中图分类号：TB 52 " " " 文献标志码：A

超声波洁牙器在口腔医学中的应用已取得了显著成效，由于频率突变和漂移问题，因此其稳定性和可靠性受到了限制，不仅影响了患者的治疗体验，还可能对治疗效果产生不良影响。

目前，传统的超声波洁牙器普遍缺少频率追踪功能。外部干扰（不同的牙质、结石、菌斑和脱矿等）或换能器内部的老化，都可能导致其无法工作在谐振频率，从而降低输出效率、振幅变小，进而降低清洁质量，增加牙齿损伤的风险。因此，在设计具有频率追踪功能的新型设备阶段，需要考虑其多变的工作状态和特性，并设计合适的追频算法以保证追频效果。

截至2023年底，频率追踪技术方面的研究已提出了多种方法，包括电流最大法、电压最小法、阻抗最小法以及复合追频法等[1-5]。然而，现有的单一追踪方法普遍存在追踪精度不高、抗干扰能力较差等问题。

为了解决超声波频率追踪技术中的问题，本文提出了一种基于变步长微分控制的最大电流法，并将其与相位检测法相结合，形成了一种新的复合控制方法。针对医用口腔超声波洁牙器的工作特点，笔者设计了新设备，旨在提高设备的可靠性和有效性，从而为超声波技术在口腔医疗方面的应用提供参考。

1 方法

1.1 压电换能器阻抗特性分析

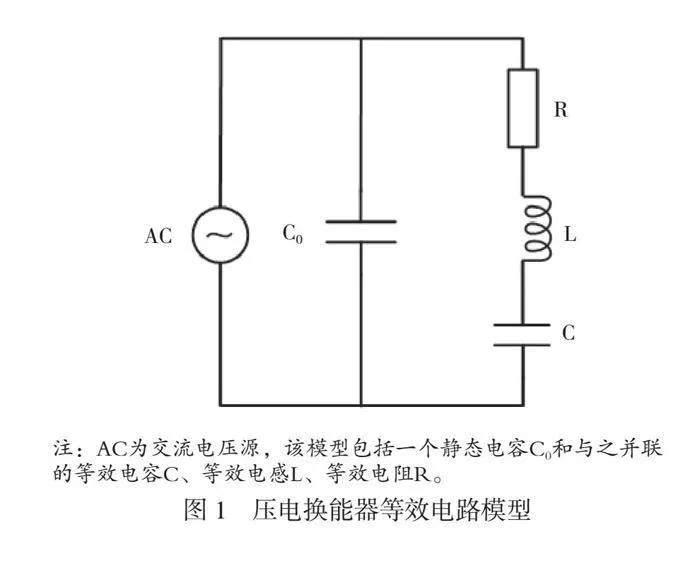
在压电换能器的等效电路模型（如图1所示）中，串联支路包括与频率相关的等效电容C、等效电感L和等效电阻R。在特定的谐振频率下，电容性阻抗和感性阻抗的数值相等但是符号相反，从而相互抵消。此时，电路等效为电阻，输入阻抗最小，电压与电流相位相同，输入电流达到最大值。这个特定频率就是压电陶瓷的谐振频率。当压电陶瓷工作时，通过施加交变电场使其周期性振动，从而实现能量的互换。选择合适的工作频率，使其接近谐振频率，可以最大程度地提高压电陶瓷的工作效率。

1.2 最大电流法频率追踪

最大电流法频率追踪是一种用于超声波换能器的频率控制方法。通过调节输入电流，使换能器在谐振频率附近工作，从而实现精确的频率追踪。

1.2.1 原理

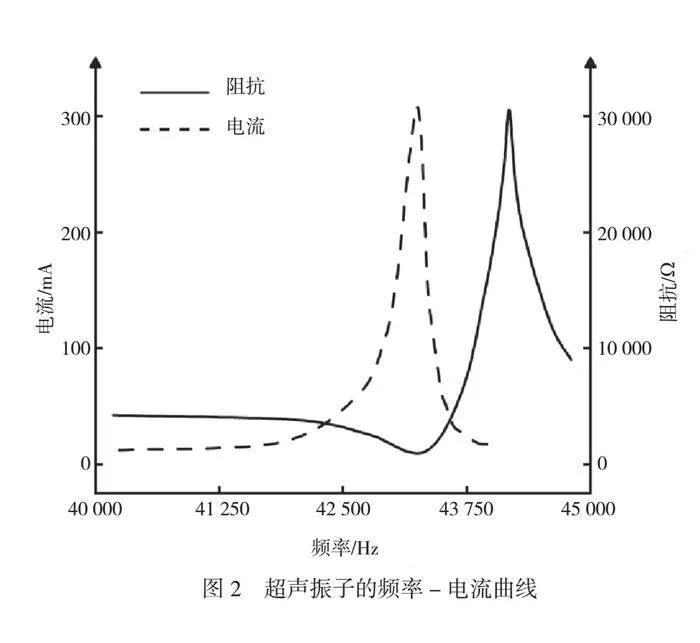
在超声波换能器中，当施加交流电压时会产生机械振动。换能器的机械振动与输入电流之间存在非线性关系。根据最大电流原理，当电源输出频率与换能器共振频率匹配时，机械振动的幅值将达到最大值。因此，通过测量换能器输出电流的幅值，可以实时跟踪其频率，并通过调节输入电流实现频率的追踪。超声振子的频率-电流曲线如图2所示。

1.2.2 优势与局限性

最大电流法频率追踪算法具有以下2个优势。1）算法步骤简单，实用性强。2）通过实时测量电流幅值，可以实现对频率变化的快速响应。

该算法存在以下2个方面的局限性。1）受换能器本身非线性特性的影响，追踪精度可能受限。2）对换能器负载变化敏感，可能影响电流幅值的测量和频率追踪效果。

1.2.3 算法步骤

最大电流法频率追踪算法包括6个步骤。1）初始化。设置初始电流值，开始试验。2）测量电流幅值。通过传感器或电流测量装置，实时监测换能器输出电流的幅值。3）比较幅值。将实时测得的电流幅值与预先设定的最大电流值进行比较。4）调节电流。根据比较结果，逐步调节电路频率，使其逐步逼近最大电流值。5）追踪频率。当电流幅值达到最大值时，换能器工作在谐振频率附近，即可认为频率追踪成功。6）反馈控制。根据实时测得的电流幅值与最大电流值之间的差异，持续调节输入电流以实现频率的稳定追踪。

1.3 变步长算法

1.3.1 原理

变步长算法是一种自适应调节步长的优化算法。它可以根据误差函数的变化动态调整每步的搜索步长，从而实现快速有效的寻优。传统的最大电流法当实现频率追踪时通常采用固定步长。然而，由于超声波换能器的工作状态可能因不同工况而发生变化，因此固定步长可能无法满足精确的频率追踪需求。变步长算法通过实时监测换能器的频率追踪状态来动态调整步长大小，以适应不同工况下的频率追踪需求。与固定步长相比，该方法更符合超声波换能器的特性，并能对不同负载工况进行自适应调整。参考超声波换能器的阻抗特性，本文设计了一种谐振频率检测机制和相应的误差函数，以指导步长调整，实现高效稳定的变步长频率追踪。

1.3.2 变步长最大电流追频算法流程

变步长算法在频率追踪中的流程如图3所示。初始化频率扫描的上下限Freqmax和Freqmin，并将当前频率设定为最小频率。然后，进入迭代调谐过程，根据当前频点的电流值I和电流对频率的微分值dI来动态调整下一步的步长Δy。

如果Ilt;预设的阈值1，就说明当前频率远低于谐振频率，须采用大步长δ来加速逼近目标频率。

如果I较大且dIgt;0，那么以电流对频率的微分值为自变量的变步长函数来确定ε，才能更精细地进行调谐。计算过程如公式（1）所示。

（1）

式中：α、β为步长极值参数；σ、μ为曲线形状横向调节参数。在实际应用中，可以根据设备处理器精度来选择ε的多项式近似拟合函数，以降低运算复杂度。

如果dIlt;0，则计算电流最大值Imax与当前I的差值是否﹥阈值2。如果是，就说明已找到谐振频率，结束扫频程序。

返回最后确定的谐振频率。通过上述自适应变步长过程，可以快速精确地锁定谐振频率。

1.4 复合控制策略

为提高追踪精度，确保超声波洁牙器在工作中遇到快速变化的负载时能够及时调整谐振频率，本文将最大电流法与相位检测法相结合。在扫频程序结束后，利用相位检测法来实现后续的频率追踪。相位检测法通过跟踪锁相环内的电流与电压相位来锁定振子频率，具有精度高、响应快、稳定性高和易于实现等优点[6-7]。然而，由于超声换能器存在多个谐振频率点，单纯的相位检测法无法直接锁定未知振子的谐振频率[8]，因此其效果并不理想。为了解决这个问题，本文首先采用最大电流法来确定谐振频率，随后在确定的谐振频率附近使用相位检测法来跟踪相位差。

锁相技术能有效抑制噪声干扰，而最大电流法则辅助判断谐振频率。此外，通过引入变步长算法，实现了自适应频率调谐。这三者相互协同工作，形成了稳定的复合控制策略。

2 试验

为验证所提出方法的有效性，本文搭建了模拟测试平台，该平台包括信号发生器、鉴相器和峰值电流检测电路等模块。笔者向压电换能器输入不同频率的信号进行测试，并记录响应电流值，从而得到频率-电流曲线。如图3所示。

从图4（峰值电流检测电路）可以看出，输入信号经过二极管进行半波整流后为充电电路充电，二极管在正半周期导通，负半周期截止，使电容可以存储正半周期的峰值电压。3.3 μF电容储存的峰值电压被送入模数转换器进行采集，以实时检测信号中的最大电流值。同时，在设计中并联了一个电阻R（阻值为10 kΩ），使电容可以持续放电，从而实现动态捕捉最大电流的功能。通过该电路，可以在频率扫描过程中测量每个频点的电流峰值，为锁定谐振频率提供依据。

3 结果

图5（a）显示了当频率未达到共振频率时，超声振子的电流和电压信号以及二者的相位差；采用本文提出的算法进行频率追踪后，对应的结果如图5（b）所示。可以明显看出，频率追踪后，电压和电流之间的相位差明显变小，并趋近于零。此时，超声振子呈纯阻性。这说明本文所设计的频率追踪算法能够有效地校正相位差，使输入频率逼近输出信号的谐振频率，从而验证了该算法的有效性。

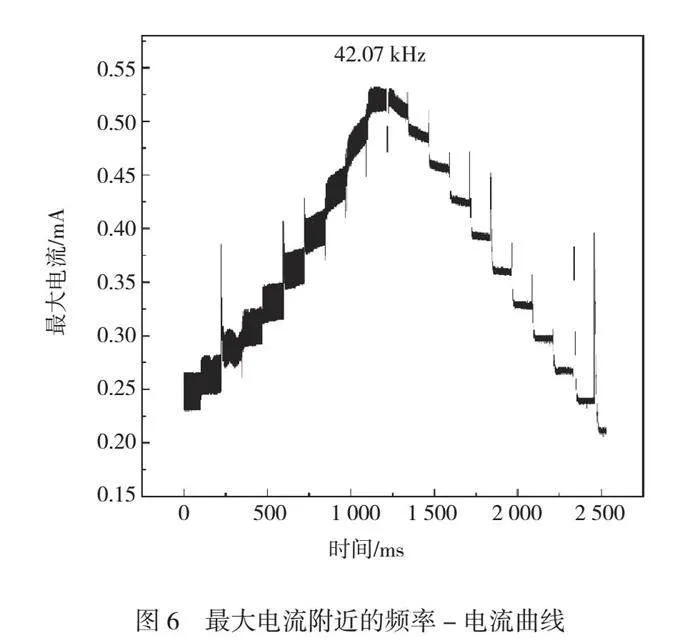
对频率逐步扫描，并记录不同频率下的电流值，获得了频率-电流曲线（如图6所示）。从图6中可以看出，本次试验所采用的超声振子在输入频率为42.07 kHz的信号下，振子电流达到最大值。这说明在这个频率下该振子的阻抗最低，因此，此时锁定的频率即为超声换能器的谐振频率。

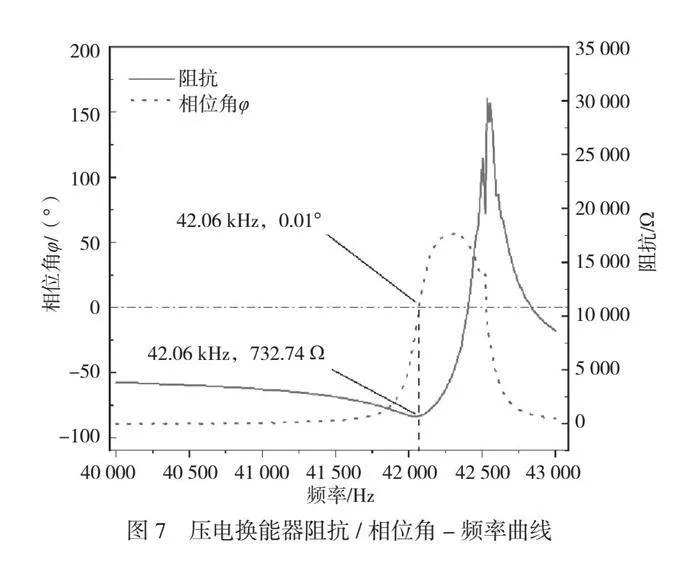
图7为测试所用压电换能器的阻抗和相位角随频率变化的曲线。测得该换能器的谐振频率为ƒp=42 064 Hz，与用最大电流法测得的42.07 kHz一致，进一步验证了该算法的有效性。可以看出，在谐振频率附近，压电换能器的阻抗最小，相位角接近0，这与理论分析和等效电路模型相吻合。后续工作将集中在提高该控制算法的鲁棒性上，以适应现实中更复杂的工作环境。

4 结语

本文针对传统超声波洁牙器无法追踪随负载工况变化的共振频率的问题，提出了一种基于最大电流法的变步长微分控制算法，通过相位检测辅助实现频率追踪功能。仿真试验证明，该算法能够在较大频率范围内锁定所用超声换能器的共振频率，并在不同负载条件下稳定工作在谐振频率附近，从而有效地提高了超声波洁牙器的清洁效率和控制精度。未来，笔者将进一步在实际设备上验证该算法的有效性，并探索更多先进的控制算法，为新一代超声波洁牙器的研发和应用提供参考。

参考文献

[1]范鹏，周俊雄，刘子源，等.超声波频率追踪方法综述[J].电声技术，2022，46（8）：1-5.

[2]候光华，杜贵平，罗杰.超声波电源的改进频率跟踪方法[J].电源学报，2019，17（1）：152-158.

[3]杜劲超，罗辞勇，肖洪伟，等.基于最小电压法的超声换能器谐振频率自动跟踪[J].应用声学，2013，32（5）：336-340.

[4]左传勇.超声换能器并联谐振频率自动跟踪系统研究[D].上海：上海交通大学，2022.

[5]刘丽晨，杨明，李世阳，等.超声换能器并联谐振频率的复合式跟踪方法研究[J].应用声学，2015，34（1）：45-50.

[6]尉茜，成志新，韩爱民.新型超声发生器中锁相环的研究[J].中国辐射卫生，2018，27（5）：511-512.

[7]左传勇，杨明，李世阳.基于电流和相位差的超声换能器频率自动跟踪[J].应用声学，2016，35（3）：189-194.

[8]成志婕.脉冲式超声波发生器频率自动跟踪技术的研究[D].太原：中北大学，2021.

通信作者：马树军（1982—），男，博士生导师，研究方向为微/纳机电系统（M/NEMS）的驱动和感知。

电子邮箱：mashujun@me.neu.edu.cn。