煤矿带式输送机能耗影响因素分析及节能设计研究

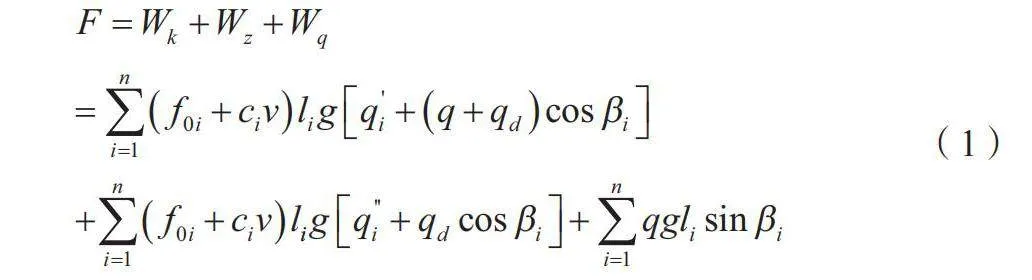
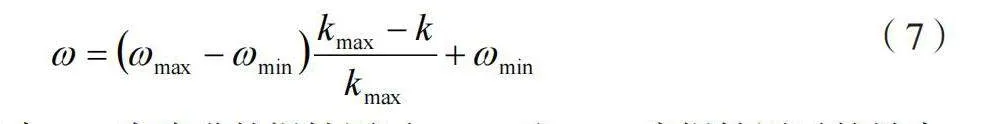
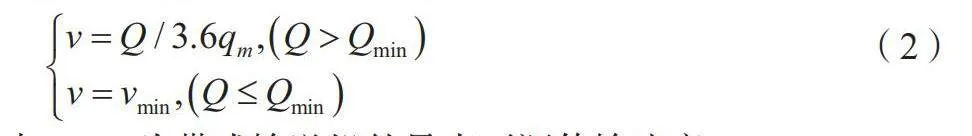
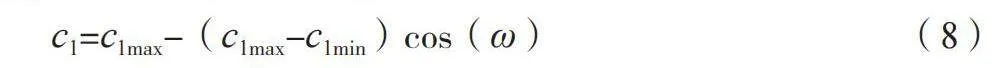
摘 要：煤矿带式输送机具有运量大、能耗高的特点，为了实现低碳生产，首先分析了造成输送机高能耗的原因，确定了煤流量和运行速度2个主因。其次，利用BP神经网络算法构建输送机节能控制模型，将煤流量和运行速度作为输入层节点，电机工作频率作为输出层节点，并且运用改进粒子群算法优化节能控制模型中的权重和阈值，提高了模型的收敛速度，降低了模型对训练数据的要求，借助该控制模型获得不同煤流量下的最佳带速取值。最后，从工程应用的角度出发，通过模糊控制器将节能控制模型引入带式输送机的控制系统，实现了算法落地。

关键词：煤矿带式输送机；能耗影响因素；节能设计

中图分类号：TD 63" 文献标志码：A

煤矿带式输送机节能控制属于较复杂的系统性问题，其影响因素较多，需要确定主要因素和次要因素，再根据主因制定节能运行方案。神经网络算法用于分析、解决复杂问题，能够通过数据训练建立能耗影响因素和电机工作频率之间的最优关系，因此利用这类算法设计节能控制模型。

1 煤矿带式输送机能耗影响因素分析

1.1 煤矿带式输送机的结构及工作原理

1.1.1 结构组成

带式输送机的主要结构包括机架、转向滚筒、驱动滚筒、托辊、卸料漏斗、张紧装置以及传送带等，其动力装置为电机，通过减速器、制动器控制速度[1]。托辊为传送带及物料提供支撑力。张紧装置的作用是防止皮带张力不足。驱动滚筒将电机产生的机械能转化为皮带的动能，转向滚筒能够控制皮带的转动方向。

1.1.2 工作原理

在带式输送机中的前后端分别设置驱动滚筒和转向滚筒，传送带为环形封闭结构，套在滚筒外侧，并且滚筒和传送带之间紧密贴合，形成了较大的摩擦力。当电机产生的动力作用在驱动滚筒时，滚筒转动，再由摩擦力带动传送带[2]。显然，只有当滚筒和传送带的摩擦力小于驱动滚筒的转动力时，才能确保传送带不打滑，并完成物料输送任务。

1.2 能耗影响因素分析

1.2.1 运行阻力分析

1.2.1.1 基本阻力

传送带系统运行时受多种阻力影响，降低传送效率及设备寿命。基本阻力主要来源于传送带与托辊、煤炭物料间的摩擦力。这些摩擦力导致传送带速度降低、能量损失并产生热量，加剧磨损，影响使用寿命。

1.2.1.2 倾斜阻力

带式输送机易受环境和地基的影响，形成倾角，产生倾斜阻力。输送带与传动滚筒间摩擦力分布不均也是倾斜阻力原因之一，导致输送带磨损加剧，缩短使用寿命。

1.2.1.3 附加阻力

工业生产中，附加阻力主要来源于驱动滚筒、改向滚筒和落料区。驱动滚筒受物料摩擦力、自身惯性和外部环境的影响；改向滚筒需要克服物料惯性和外部环境的影响；落料区物料受重力作用产生阻力，影响物料下降速度和生产线的运行效率[3]。

1.2.2 造成功率消耗的主要影响因素

在煤矿开采过程中，随着掘进面不断深入，带式输送机的传输距离持续增加，能耗呈快速增长的趋势。以大运量、高转速、长距离的带式输送机为研究对象，造成其功率消耗的影响因素如下。

1.2.2.1 确定主要因素

将带式输送机的牵引力记为F，如公式（1）所示。

（1）

式中：Wk为带式输送机在回程段的基本阻力；Wz为承重段的基本阻力；Wq为输送机的倾斜阻力；f0i为关于输送机速度的系数；ci为与输送机速度有关的系数；v为输送机的传输速度；li为输送带的长度；g为重力加速度；qi'为托辊的旋转线密度；q为煤炭物料的线密度，并且有q=Q/3.6v（Q为煤流量）；qi\"为回程段托辊组的旋转线密度；qd为输送带的线密度；βi为巷道的倾角。

在计算出牵引力F后，可按照P=Fv得到带式输送机的功率（P为功率）[4]。

例如，某煤矿购入的带式输送机，工作人员根据公式（1）计算器能耗（见表1）。

假设煤流量Q=500，输送机的输送量为500/3600。kg/h，即输送机的输送量为0.1389kg/s，q=0.1389/3.6×2.5=0.0198kg/m，计算重力牵引力为0.0198×1000×cos（5°）=188.6N；摩擦力为（0.1+0.08）×6×9.81×1000×cos（5°）=367.6N；总牵引力为200+350+150+0.02×2.5+0.0015×（2.5）2，即F=700.059375N。

1.2.2.2 带速与煤流量匹配分析

当带式输送机处于正常的运行状态时，如果煤流量Q保持不变，那么功率P与带式输送机的传输速度v成正比。在这一情况下，提高速度v会增加功耗[5]。但是输送机的速度不可过低，否在会制约生产效率。将传送带能够承受的最大物料线密度记为qm，煤流量最小值记为Qmin，则煤矿传输带的速度v应满足公式（2）的规定。

（2）

式中：vmin为带式输送机的最小可调传输速度。

分析公式（2）可以发现，煤矿传输带的速度与功率成正比，影响功耗和生产效率的平衡，同时需要满足输送带能够承受的最大物料线密度和最小煤流量的要求。因此，应用速度v的计算公式时，需要根据具体的系统设计参数和操作条件来确定合适的速度范围，以确保系统运行效率和安全性。

2 煤矿带式输送机节能控制模型设计

带式输送机的节能控制属于较复杂的系统性问题，需要从系统功耗出发，合理确定煤流量与传输速度的取值，根据生产需求自动调节煤流量和传输速度，从而达到功耗最低的目标。以下基于BP神经网络和改进粒子群算法建立和优化带式输送机节能控制模型，再通过PLC模糊控制器实现算法模型，达到智能调节的目的。

2.1 基于BP神经网络的带式输送机节能控制建模

2.1.1 BP神经网络模型概述

一个典型的BP神经网络包括3层结构，分别为输入层、隐藏层和输出层，输入层为待研究问题的主要影响因素，输出层为研究目标，隐藏层在二者之间建立联系[6]。将输入层节点、隐藏层节点和输出层节点分别记为xi、yj、zk，三者之间的关系如公式（3）所示。

（3）

式中：f（）为隐藏层的激活函数；wij为输入层节点xi与隐藏层节点yj之间的权值；θj为隐藏层节点j的阈值。

输出层节点与隐含层节点之间的关系如公式（4）所示。

（4）

式中：T1i为隐藏层节点与输出层节点对应的权值。

其中，激活函数f（）可采用Sigmoid函数。

在BP神经网络的隐藏层中，每个隐藏层节点yj的输出如公式（5）所示。

（5）

式中：wij为输入层节点xi到隐藏层节点yj的权重；θj为隐藏层节点yj的阈值。

Sigmoid函数的作用是将加权和z映射到一个在（0，1）的值，这种非线性映射使神经网络能够学习和表示复杂的非线性关系。在BP神经网络的输出层，如果网络用于分类问题，通常也会采用Sigmoid函数作为输出层的激活函数，输出层节点zk如公式（6）所示。

（6）

式中：Tjk为隐藏层节点yj到输出层节点zk的权重；θk为输出层节点zk的阈值。

在使用Sigmoid函数过程中，要着重注意2个问题。一方面，Sigmoid函数在输入接近极端值（接近0或1）时，其导数接近0，可能导致梯度消失问题，这会影响神经网络的训练效果。另一方面，Sigmoid函数的输出范围为（0，1），可能不适用于某些问题，例如需要输出负数或超过单位间隔的值。

2.1.2 带式输送机节能控制模型构建及训练

2.1.2.1 训练样本采集

建模前需要收集模型训练所需的数据，以煤矿带式输送机的实际运行情况为数据源，当煤流量较稳定时，检测该时段对应的煤流量，并求出均值，记为Qavg。调节输送机的电机频率，进而改变带式输送机的传输速度，将输送机的最小可调速度和最大可调速度分别记为vmin、vmax，使输送机的速度从最小值逐渐增至最大值，在这一过程中观察功率P的变化，将最小功率记为Pmin，并记录该功率对应的速度。研究过程按照以上方法检测获得60组试验数据，在不同时段内得到3组煤流量均值，分别为Qavg1、Qavg2、Qavg3，3种煤流量下对应的最小功率分别为Pmin1、Pmin2、Pmin3，最小功率对应的速度分别记为v1、v2、v3。

2.1.2.2 模型构建及训练

当构建和训练模型时，需要编写相应的程序。研究过程利用MATLAB软件构建BP神经网络模型，输入层设置2个节点，分别代表煤流量和带式输送机的传输速度，输出层设置1个节点，即电机功耗，目标是获得特定煤流量下的最低功耗及其对应的输送机速度。根据隐含层节点数量的计算方法，该模型需要设置5个隐藏层节点。利用60组试验数据进行模型训练。

2.2 基于粒子群算法优化节能控制模型

2.2.1 改进粒子群算法

2.2.1.1 粒子群算法

改进粒子群算法是在粒子群算法（Particle Swarm Optimization，PSO）的基础上进行改进的。PSO算法用于复杂问题智能寻优，其实施步骤为种群初始化→计算种群中个体的适应度值→更新粒子个体的最优位置→根据适应度值进行复制→判断是否满足终止条件，满足时终止算法，否则回到第二步。

2.2.1.2 粒子群算法的改进

PSO算法中的参数具有一定的经验性，缺乏客观的依据，容易影响算法的精度，相关的参数为惯性因子和学习因子，改进方式如公式（7）所示。

（7）

式中：ω为改进的惯性因子；ωmin和ωmax为惯性因子的最小值和最大值；k为惯性因子的调节系数；kmax为调节系数的最大值。

在改进方法中，通过公式（7）提高惯性因子的自适应能力。公式（7）通过线性插值的方式，根据k和kmax的比例，使ω在ωmin和ωmax之间动态调整。当k=0时，ω=ωmax，当k=kmax时，ω=ωmin。传统PSO算法中存在c1、c22个加速学习因子，通常取为定值，在改进粒子群算法中，按照公式（8）计算加速学习因子的取值。

c1=c1max-（c1max-c1min）cos（ω） （8）

式中：c1max和c1min分别为加速学习因子c1的最大值、最小值，c2的计算模式同c1。

通过线性插值的方式，根据k和kmax的比例，动态调整c1和c2的取值范围。这种动态调整有助于在PSO算法中自适应地改变加速学习因子，以便更好地探索和利用搜索空间。

2.2.2 基于改进PSO算法的节能控制模型优化

2.2.2.1 模型优化步骤

利用改进PSO算法优化煤矿带式输送机的节能控制模型，其实施步骤如下。1）粒子群和节能控制模型的初始化。2）计算每一个粒子的适应度值，对比个体适应度值，确定全局最优值。3）计算改进的惯性因子ω和学习因子c1、c2。4）利用改进的惯性因子和学习因子更新粒子群算法中的个体，获得最新的位置和速度。5）更新个体及全体最优值。6）判断是否满足条件，结束迭代操作。

2.2.2.2 模型优化结果分析

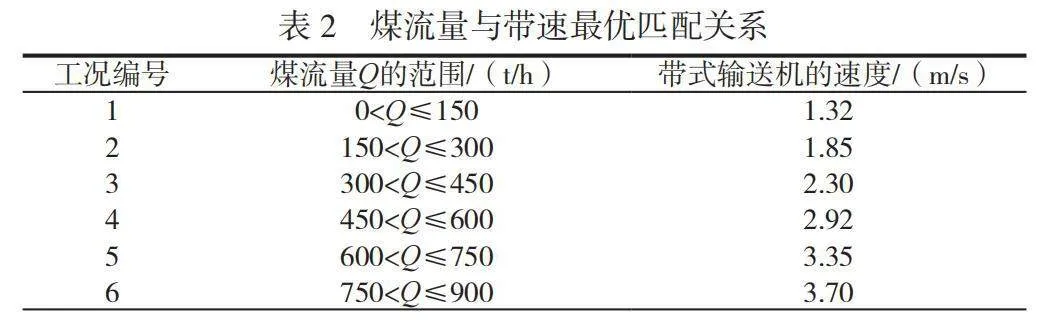
分别利用传统PSO算法和改进PSO算法优化PB神经网络所建立的节能控制模型，得到算法模型中最佳的权值和阈值，共进行50次迭代。结果显示，经传统PSO算法优化的模型在第24次迭代时完成收敛，而改进PSO算法优化的模型在第16次时完成收敛。说明改进PSO算法提高了节能控制模型的运行效率，并且后者对模型训练数据量的需求也更低。利用节能控制模型得到煤流量与带式输送机最佳速度的关系，见表2。

3 带式输送机节能控制系统模糊控制器设计

在建立节能控制模型后，还需要以特定的方式将其植入带式输送机的控制系统中，研究过程利用模糊算法及模糊控制器实现相关功能。

3.1 模糊控制器基本原理

模糊控制器由知识库、推理库组成，将给定信号输入控制器后，先进行模糊化处理，再经过模糊推理，产生清晰化的信号，进而作用于被控制的对象，整个过程由传感器实时获得被控变量，并反馈至输入端。

3.2 模糊控制设计要点

3.2.1 模糊控制器的输入和输出设计

从上文的分析可知，在煤流量确定的情况下，节能控制的关键是确定与之匹配的最佳带速。将模糊控制器引入节能控制模型，带式输送机具有电子称量功能，可检测煤流量，与其对应的速度记为v0，利用传感器采集皮带速度v，计算v0和v的偏差e，同时计算对应时间段内的偏差变化率ec，将e和ec输入模糊控制器，模糊控制器的输出结果为变频器的频率f。

3.2.2 设置模糊论域和比例因子

在模糊控制器中，变量e、ec、f对应的符号为E、EC、F。针对这3个变量设置相同的模糊论域{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}。3个变量的迷糊集见表3。3个变量对应的比例因子分别记为ke、kec、kf，则有ke=6/e，kec=6/ec，kf=6/f。

3.2.3 模糊控制表查询

在速度传感器检测出偏差e和偏差变化率ec后，再根据模糊控制表查询相应的频率f，进而完成模糊输出与控制。根据论域、比例因子、模糊控制规则等，设计模糊控制表，见表4。此处仅展示模糊论域中-1～-6的取值，表格中的数值为f的取值。

3.2.4 模糊控制系统整体实现

模糊控制系统的整体工作流程如下：获得给定值v0，对比传感器检测速度v→将偏差e和偏差变化率ec输入模糊控制器→输出电机频率f→由PLC控制器发出信号，控制变频器→将信号f作用于电机→改变皮带运行速度。

4 结语

从研究内容可知，影响煤矿带式输送机能耗水平的主要因素为煤流量和皮带运行速度，在煤流量确定的情况下，存在一个最佳带速，能够使电机功耗最低。研究过程利用BP神经网络建立带式输送机节能控制模型，并且借助改进PSO算法优化模型中的关键参数，进而确定不同煤流量范围下的最佳带速取值。本文还设计了相关的模糊控制器，可以将其引入PLC变频控制系统中，以实现节能控制模型的工程应用。

参考文献

[1]王利国.煤矿带式输送机能耗优化控制系统的设计与应用[J].矿业装备，2023（9）：204-205.

[2]范惠凯.变频节能系统在带式输送机中的应用研究[J].石化技术，2023，30（7）：275-276.

[3]王循明，单岩，张炜.基于模糊PID的液压驱动带式输送机能耗优化[J].煤炭技术，2023，42（5）：207-209.

[4]蒋思中，郭宏涛，安轲，等.基于PSO-BP神经网络的带式输送机能耗优化研究[J].煤炭技术，2022，41（11）：234-236.

[5]刘宪兵，张伟.矿井带式输送机节能控制系统研究[J].内蒙古煤炭经济，2023（5）：69-71.

[6]马晓琳.基于计算机视觉技术矿山运输智能调速控制系统研究[J].中国矿山工程，2021，50（5）：67-70.