基于SMA-BP算法的焊件动态电阻预测

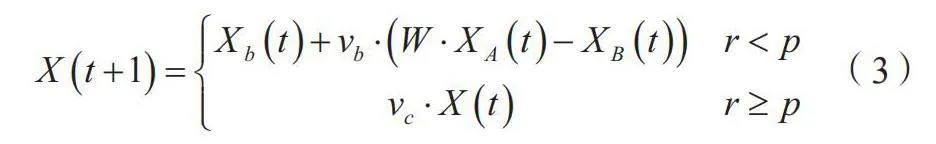
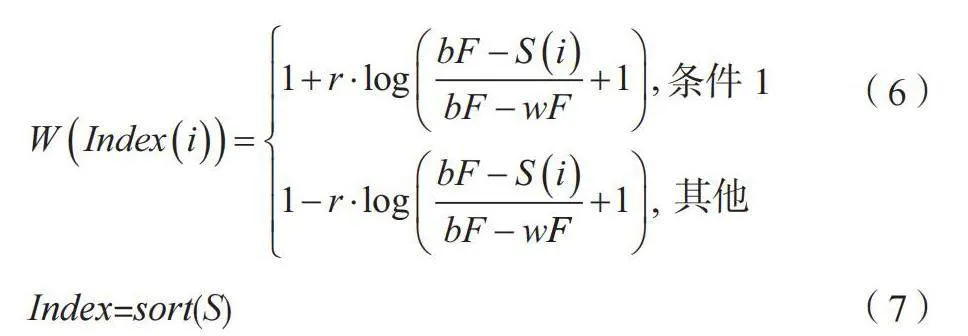
摘 要：在电阻点焊过程中焊点的形成涉及多个物理量的变化，不能精确描述。因此，本文采集标准焊点的焊接数据，建立基于黏菌算法-BP神经网络（Slime Mould Algorithm-Back Propagation Neural Network，SMA-BP）的焊点动态电阻预测模型。将当前时刻的电极累计释放的热量与动态电阻作为预测模型的输入，下一时刻的动态电阻作为模型的输出。结果表明，经黏菌算法优化后的BP神经网络在测试集上的决定系数R2、均方误差（MSE）、均方根误差（RMSE）和平均绝对误差（MAE）均优于单一的BP模型，给电阻点焊控制器的设计提供参考。

关键词：电阻点焊；电阻预测模型；黏菌算法；神经网络

中图分类号：TG 441" " " 文献标志码：A

电阻点焊是一种广泛应用于汽车制造、航空航天等工业领域的制造工艺。但是电阻点焊的焊接时间较短且易受干扰，因此精准控制焊接过程比较困难。目前，相关学者开始研究焊点电阻变化与焊接过程的联系。例如李健等[1]提出了基于FFRLS的电阻点焊预测模型。董建伟等[2]使用麻雀搜索算法改进BP神经网络，将电阻点焊过程中的工艺信号特征作为输入信号来预测焊点的焊接质量。袁孝杰等[3]使用遗传算法并结合BP神经网络，以焊接功率特征量作为输入，预测焊点的质量。在前人的基础上，本文将黏菌算法与BP神经网络相结合，建立了黏菌算法-BP神经网络模型，以预测焊点的电阻变化。

1 SMA-BP神经网络模型

1.1 BP神经网络

BP神经网络是目前应用最广泛的人工神经网络模型。它是模拟人类大脑对信息处理的过程建立的一种黑盒模型。由于不必利用精密的数学方程即可得到较准确的预测值，因此被广泛应用于各种非线性关系的预测中[2]。

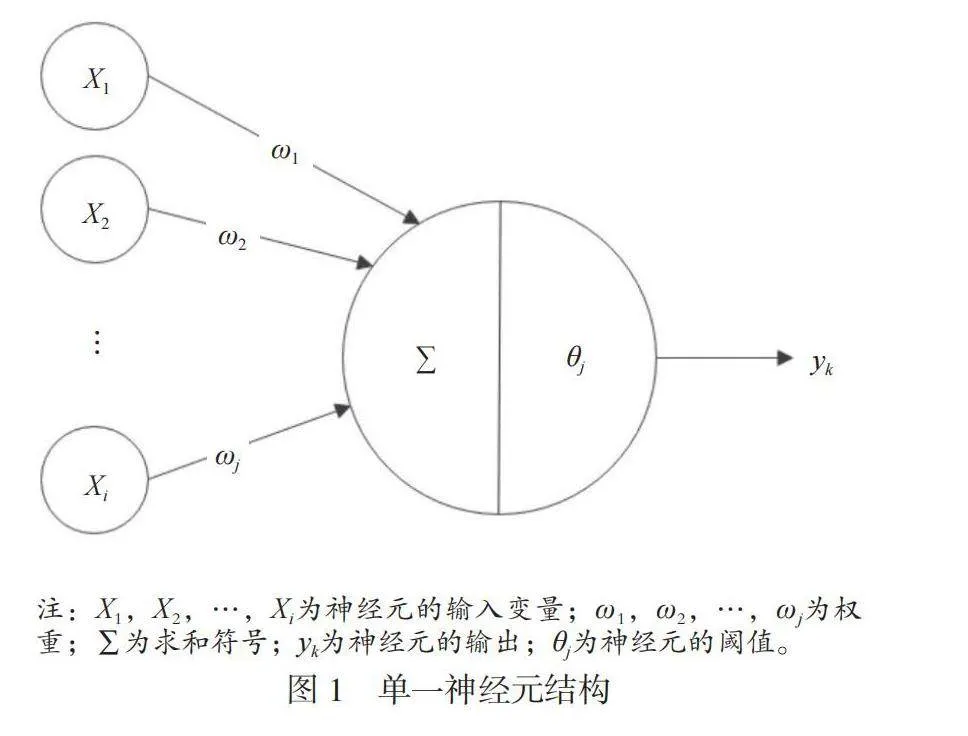
BP神经网络中单一神经元的结构如图1所示。其中神经元的总输入如公式（1）所示。

（1）

式中：Netin为神经元的总输入；f（）为激活函数。

Netin先与θj比较大小，再由激活函数决定神经元是否输出。将BP神经网络与点焊实际应用相结合，建立BP神经网络预测拓扑结构，如图2所示。

BP神经网络结构由输入层、隐含层和输出层3个部分组成。输入量为焊极累计释放的热量与当前时刻的焊件电阻值，输出量为下一时刻的焊点电阻值，隐含层神经元数量hiddennum则由经验公式给出，如公式（2）所示[2]。

（2）

式中：m为输入层节点数；n为输出层节点数；b为1～10的自然数。

BP神经网络的学习规则是使用最速下降法，利用反向传播来不断修改网络的权值和阈值，最终提高预测的准确度。因此BP神经网络预测的精度与稳定性是由初始权值和阈值决定的。但是在初始化过程中，初始权值和阈值都是随机的，导致预测的精准度波动较大，因此本文引入具有优良全局寻优能力的黏菌算法来优化BP神经网络的初始权值和阈值。

1.2 黏菌算法

黏菌算法（SMA）是2020年经模拟黏菌捕食行为提出的一种全新的群智能算法[4]。在觅食移动过程中，黏菌前端会形成一个扇形区域，静脉结构与主体相连接，细胞质会在其间流动。黏菌会分析目标区域的食物浓度，调整静脉网络的厚度。食物源的浓度越高，黏菌生长就越快，形成的静脉网络也就越粗。当食物源浓度较低时，黏菌将调整方向，最终形成连接食物的最佳路径。黏菌的觅食移动主要包括接近食物、包裹食物与生物振荡3个部分[5]，黏菌算法的具体步骤如下所示。

首先，黏菌会切割出一部分个体，对潜在的食物进行随机搜索，可以用数学模型表示，如公式（3）所示[6-7]。

（3）

式中：t为当前的迭代次数；t+1为下一次迭代；Xb为当前时刻食物浓度最高的黏菌个体位置，即最优解的寻优方向；Xb（t）为当前迭代次数下食物浓度最高的黏菌个体位置，即最优解的寻优方向；vb为模拟黏菌觅食时的收缩扩张，其在

[-a，a]随机波动，a为vb波动范围的上、下限，并且随着迭代次数增加而逐渐趋近于0，a的计算过程如公式（4）所示；W为权重系数，如公式（6）、公式（7）所示；XA、XB分别为当前黏菌群落中随机2个个体的位置；XA（t）、XB（t）分别为当前迭代次数下，黏菌群落中随机2个个体的位置；r为[0，1]的随机数；p为黏菌位置的更新开关，如公式（5）所示；vc为模拟黏菌接近食物的过程，其在[-1，1]振荡，最终趋近于0；X（t）为当前时刻黏菌的所在位置。

（4）

式中：tmax为最大迭代次数，在算法初始化过程中进行设置。

p=tanh|S（i）-DF| （5）

式中：S（i）为黏菌个体适应度排序中第i个黏菌个体的适应度；DF为目前发现的最佳适应度。

（6）

Index=sort（S） （7）

式中：W（Index（i））为适应度按升序排序后的第i个黏菌个体的权重系数，主要用来模拟黏菌静脉宽度与食物源浓度间的正、负反馈机制，食物浓度高，权重系数W增大，反之则减少；Index为计算种群个体适应度值后对其进行排序；r为[0，1]的随机数；bF和wF分别为当前迭代中的最优适应度与最差适应度；条件1为适应度排序后对位于前一半的黏菌个体执行此计算；其他为其他个体执行其他计算；sort（）为排序函数；S为S（i）的集合。

其次，黏菌可以包裹食物。此时每个黏菌个体都会根据食物浓度微调自己的位置。根据公式（6）可知，高浓度食物附近的黏菌个体会得到较大的权重，较小浓度食物附近的黏菌个体则会探索其他区域。黏菌根据觅食区域食物浓度来调节个体的质量，从而包裹食物，如公式（8）所示。

（8）

式中：rand为[0，1]的随机数；UB和LB分别为搜索区域的上、下边界；z为自定义参数，一般取值为0.03[6-7]。

包裹食物后，黏菌生物振荡器会调节细胞质的流动，即公式（8）中W、vb和vc这3个参数迭代计算中的协同交互。

综上所述，黏菌算法的算法流程如下所示。1） 初始化参数。初始化的内容主要包括种群数量N；最大迭代次数tmax；搜索空间的上、下边界UB与LB；随机初始化黏菌个体的位置{Xi|i=1，2，...，N}。2） 计算每一个黏菌个体的适应度，进行排序，同时记录最佳个体的位置和适应度值并进行迭代。3） 在不断迭代中找寻找目标函数误差的最优参数。一旦满足条件，立刻结束迭代，输出最优参数，否则一直迭代到最大迭代次数后，输出目前的最优参数。

1.3 SMA-BP神经网络模型

将黏菌算法与BP神经网络相结合，使用满足误差要求的最优预测模型对下一时刻的焊点电阻值进行预测。SMA-BP模型流程如图3所示。

根据图3所示，先将采集的焊接数据进行数据预处理，再对SMA算法进行初始化和迭代计算。得到满足设定条件的最优参数后，将得到的最优参数赋值给BP神经网络的初始值与阈值，并对BP神经网络进行模型训练，最终得出满足目标误差要求的最优模型。

2 仿真试验

2.1 焊点数据获取

标准焊点数据来自DP590高强度双相钢的焊接试验。焊接实验平台为自制的中频电阻点焊机，焊接电流为5 kA，焊接时间为400 ms。

2.2 焊件电阻值预测

将采集的焊接数据分成训练集与测试集，在MATLAB中进行预处理后，构建BP神经网络。BP神经网络的输入层节点数为2，输出层节点数为1，根据公式（1）设置隐含层节点数为5，因此BP神经网络的结构为2-5-1。将训练次数、学习速率和训练目标最小误差分别设置成1 000、0.01和

0.000 1，选择输入层与隐含层间的传递函数、隐含层与输出层间的传递函数。

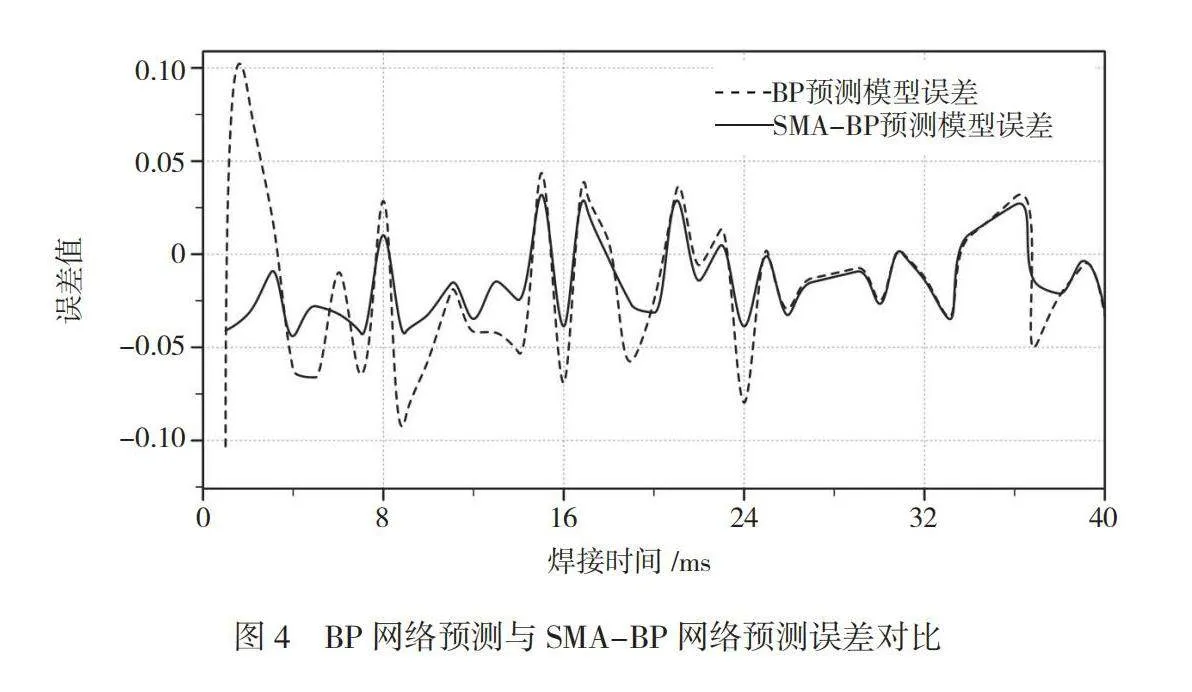
初始化黏菌算法参数。设置黏菌种群个数为50，最大迭代次数为1 000，搜索空间上界为1，下界为-1，将均方根误差作为目标函数。同时将平均绝对误差、均方误差、均方根误差和决定系数R2这4个参数作为衡量网络性能的指标。先保存训练好的模型，再把测试集数据分别输入2个预测模型中，得出的预测值与测量值误差对比如图4所示。

由图4可知，优化前的预测值与实测量值，尤其是焊接刚开始时的误差较大。当焊接刚开始时，系统为零状态响应，此时单纯的BP预测模型的预测值误差逼近±0.1，而优化后的预测值误差仅为0.02～-0.04。表明经SMA算法优化后的BP预测模型的响应速度更快。同时优化后的BP神经网络预测模型的预测值与测量值间的误差一直维持在±0.03的范围内，误差波动较小。而单纯BP神经网络预测模型误差波动一直在0.05～-0.07，误差波动较大。在图4中，为了更清楚地展示误差数据，仅截取包括焊接开始时的前40 ms的预测值与测量值的误差数据，没有将整个焊接过程中的误差数据全部展示出来。在400 ms的焊接过程中，优化前与优化后的BP神经网络预测模型的预测精度对比见表1。

由表1可知，在整个焊接过程中，经过SMA算法优化后的BP神经网络预测模型的平均绝对误差（MAE）从0.027 81

降至0.019 45，均方误差（MSE）从0.003 86降至0.002 10，均方根误差（RMSE）从0.062 12降至0.045 84，决定系数R2从0.90增至0.97，表明经过SMA算法优化后的BP神经网络预测模型的精准度得到了有效提高。

3 结语

BP神经网络的初始权值和阈值具有随机性，导致其预测能力不稳定，本文利用黏菌算法（SMA）具有参数少、寻优能力强等特点，优化了BP神经网络的初始权值和阈值，提高了原先BP神经网络的预测精度和稳定性，并在仿真中证实了优化后预测模型的精准度得到了有效提高，为电阻点焊过程中焊件的动态电阻预测提供了新的预测模型。

参考文献

[1]李建，王宾，梁立振，等.基于FFRLS的电阻点焊预测模型[J].兰州文理学院学报（自然科学版），2022，36（3）：64-67.

[2]董建伟，胡建明，罗震.基于相关性分析和SSA-BP神经网络的铝合金电阻点焊质量预测[J].焊接学报，2024，45（2）：13-18，32，129-130.

[3]袁孝杰.电阻点焊过程监测及焊点质量预测研究[D].淮南：安徽理工大学，2023.

[4]LI S M，CHEN H L，WANG M J，et al.Slime mould algorithm：A new method for stochastic optimization[J].Future Generation Computer"Systems，2020（111）：300-323.

[5]韩子萌.黏菌算法的改进及其应用研究[D].西安：西安理工大学，2024.

[6]徐岩，王若琳，胡紫琪，等.基于自适应人工蜂群黏菌算法的直流配电网故障定位的研究[J].太阳能学报，2023，44（12）：526-532.

[7]赵卿，高文华，石慧，等.基于WT和黏菌算法LSSVM短期风功率预测[J].计算机仿真，2024，41（7）：166-170，226.