这两题很难吗？

第十三届中小学数学创新应用科普活动，将于2024年9月启动报名. 本期试题来源于第十二届中小学数学创新应用科普活动，由全国青少年数学创新系列活动组织委员会提供.

更多数学创新应用优秀资源，可通过科普中国App“数学创新”科普号获取.

真题呈现

1. 某间谍机构掌握了世界上最优秀的侦探甲、乙、丙、丁、戊的部分情报，具体情况如下.

①侦探老牛的体形比侦探戊壮硕；

②侦探丁是侦探鹦鹉和侦探白狮的前辈；

③侦探乙总是和侦探鹦鹉一起办案；

④侦探甲和侦探老牛是侦探红蚁的徒弟；

⑤侦探鹦鹉的枪法比侦探甲和侦探戊的枪法更精准；

⑥侦探黑豹和侦探红蚁都曾与侦探戊发生过冲突；

⑦侦探丁是五位侦探中资历最老的.

根据上述信息，可以得出侦探乙的代号是（ ）.

A. 黑豹 B. 红蚁 C. 老牛 D. 鹦鹉 E. 白狮

2. 喜鹊、乌鸦和麻雀在树林中捉虫子，已知它们都捉到虫子了，且不多于3条. 回巢的路上喜鹊、乌鸦和麻雀分别说了一句话. 其中一只鸟说了假话，说假话的鸟捉到的虫子数量要比另两只鸟捉到的虫子的数量少，其他鸟说的都是真话.

喜鹊说：“乌鸦捉到了2条虫子. ”

乌鸦说：“麻雀捉到的虫子的数量不是2条. ”

麻雀说：“喜鹊捉到的虫子的数量不是1条. ”

那么下列说法正确的是（ ）.

A. 喜鹊1条、麻雀3条、乌鸦2条

B. 喜鹊2条、麻雀3条、乌鸦2条

C. 喜鹊2条、麻雀1条、乌鸦3条

D. 喜鹊3条、麻雀3条、乌鸦3条

E. 喜鹊2条、麻雀3条、乌鸦3条

精讲精析

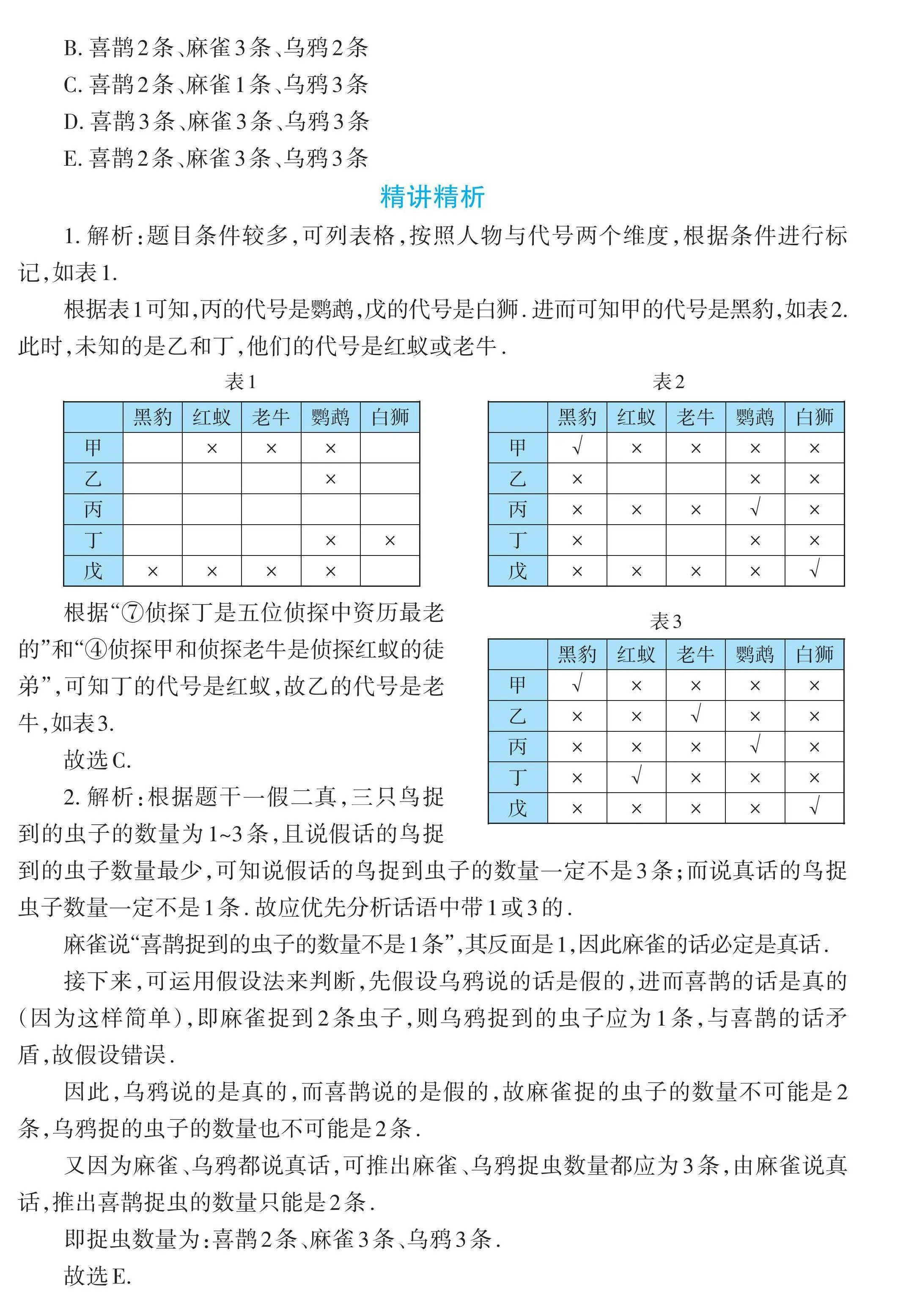
1. 解析：题目条件较多，可列表格，按照人物与代号两个维度，根据条件进行标记，如表1.

根据表1可知，丙的代号是鹦鹉，戊的代号是白狮. 进而可知甲的代号是黑豹，如表2.此时，未知的是乙和丁，他们的代号是红蚁或老牛.

根据“⑦侦探丁是五位侦探中资历最老的”和“④侦探甲和侦探老牛是侦探红蚁的徒弟”，可知丁的代号是红蚁，故乙的代号是老牛，如表3.

故选C.

2. 解析：根据题干一假二真，三只鸟捉到的虫子的数量为1～3条，且说假话的鸟捉到的虫子数量最少，可知说假话的鸟捉到虫子的数量一定不是3条；而说真话的鸟捉虫子数量一定不是1条. 故应优先分析话语中带1或3的.

麻雀说“喜鹊捉到的虫子的数量不是1条”，其反面是1，因此麻雀的话必定是真话.

接下来，可运用假设法来判断，先假设乌鸦说的话是假的，进而喜鹊的话是真的（因为这样简单），即麻雀捉到2条虫子，则乌鸦捉到的虫子应为1条，与喜鹊的话矛盾，故假设错误.

因此，乌鸦说的是真的，而喜鹊说的是假的，故麻雀捉的虫子的数量不可能是2条，乌鸦捉的虫子的数量也不可能是2条.

又因为麻雀、乌鸦都说真话，可推出麻雀、乌鸦捉虫数量都应为3条，由麻雀说真话，推出喜鹊捉虫的数量只能是2条.

即捉虫数量为：喜鹊2条、麻雀3条、乌鸦3条.

故选E.