冲击荷载下混凝土的破坏与受力分析

摘 要：为了研究冲击荷载下混凝土的破坏和受力行为，本研究采用了静态压缩试验和分离式Hopkinson杆（SHPB）进行动态冲击试验，对含黏结界面混凝土在不同应变率下的破坏程度和力学行为进行研究，并利用基于Weibull分布的本构模型对试验数据进行拟合和验证。研究结果显示，含黏结界面混凝土在不同应变率下表现出明显的动态硬化效应。强度动态提高因子呈现先增后趋于稳定的变化，而细度模数则基本稳定在1.5～1.75。然而，冲击韧性则呈现先增后减的趋势。此外，基于Weibull分布的本构模型能够较好地拟合含黏结界面混凝土在不同应变率下的应力-应变曲线。

关键词：静态压缩试验；动态冲击试验；力学行为

中图分类号：TU 52" " 文献标志码：A

混凝土结构在实际工程中经常受到地震、爆炸等冲击荷载的影响，这些荷载会对结构造成严重破坏。虽然混凝土的高强度和韧性使其在正常荷载下表现良好，但在冲击荷载下，其受力和破坏行为会发生显著变化[1]。已有大量研究深入探讨了该问题。

沈峰[2]利用近场动力学方法描述了混凝土在动载荷下的损伤与破坏过程。许斌[3]对冲击荷载下的混凝土性能进行研究。雷光宇[4]通过静态压缩试验和冲击试验分析了混凝土冲击荷载下的破坏强度。然而，目前对冲击荷载下混凝土的动态响应和力学特性的相关研究仍然较少。为了改善混凝土在冲击荷载下的性能，研究人员提出了含黏结界面混凝土的概念，并将其应用于结构工程中。但是，目前对含黏结界面混凝土在冲击荷载作用下的破坏特征和应力应变行为的研究相对有限。因此，本文旨在分析冲击荷载下混凝土的破坏与受力问题，为相关研究提供参考。

1 试验材料和试验仪器

本次研究使用的混凝土为含黏结界面混凝土，采用定制的磨具制备混凝土，磨具的半径为80mm，高度为70mm。制备时先利用定制磨具进行浇筑，待成型后在标准条件下将其养护56天后即可进行试验。

本次研究通过8802型电液伺服疲劳试验机进行静态压缩试验，设置的压缩速率为0.01mm/min，通过分离式Hopkinson杆进行动态冲击试验。

2 试验结果与分析

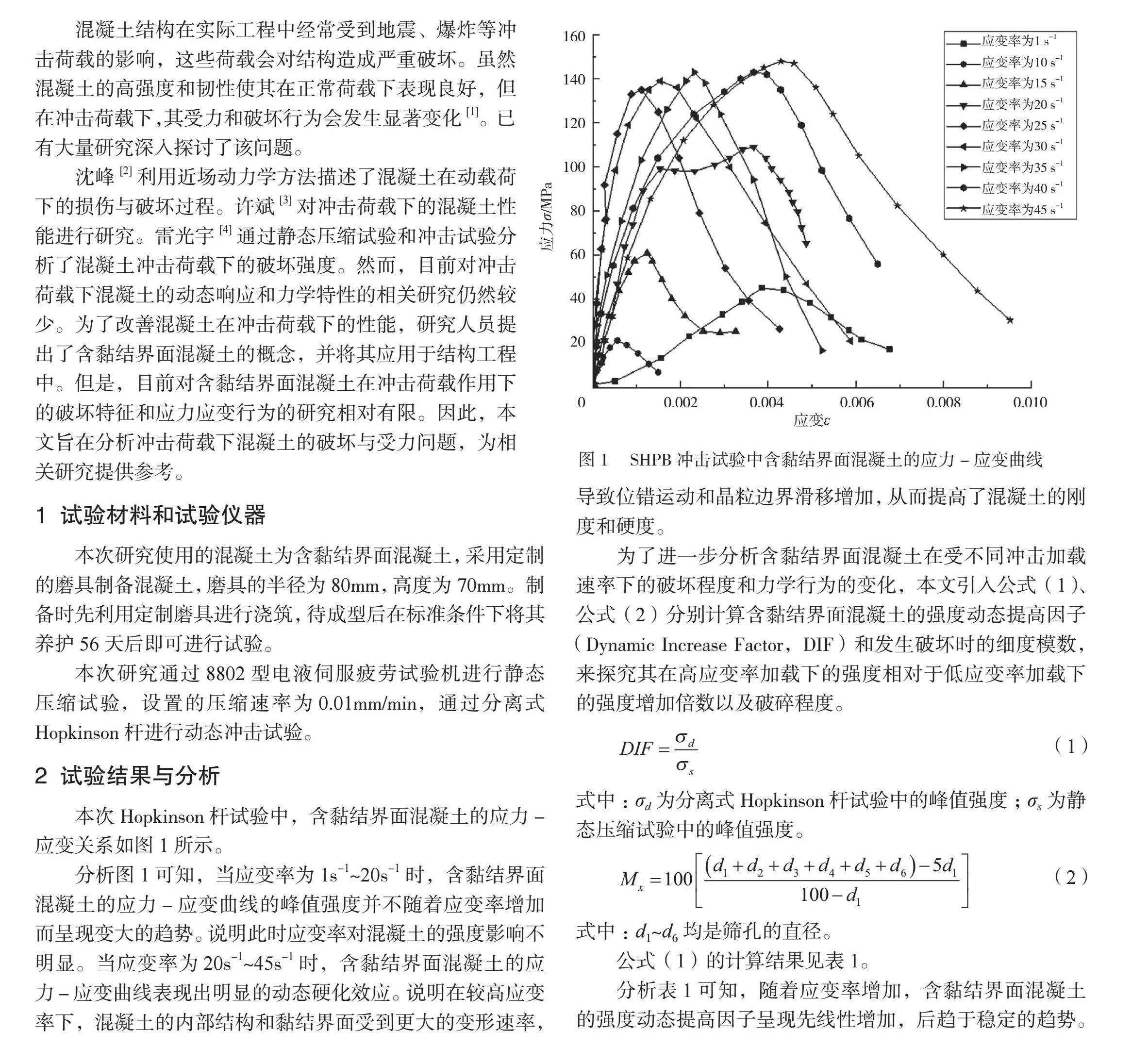
本次Hopkinson杆试验中，含黏结界面混凝土的应力-应变关系如图1所示。

分析图1可知，当应变率为1s-1～20s-1时，含黏结界面混凝土的应力-应变曲线的峰值强度并不随着应变率增加而呈现变大的趋势。说明此时应变率对混凝土的强度影响不明显。当应变率为20s-1～45s-1时，含黏结界面混凝土的应力-应变曲线表现出明显的动态硬化效应。说明在较高应变率下，混凝土的内部结构和黏结界面受到更大的变形速率，导致位错运动和晶粒边界滑移增加，从而提高了混凝土的刚度和硬度。

为了进一步分析含黏结界面混凝土在受不同冲击加载速率下的破坏程度和力学行为的变化，本文引入公式（1）、公式（2）分别计算含黏结界面混凝土的强度动态提高因子（Dynamic Increase Factor，DIF）和发生破坏时的细度模数，来探究其在高应变率加载下的强度相对于低应变率加载下的强度增加倍数以及破碎程度。

（1）

式中：σd为分离式Hopkinson杆试验中的峰值强度；σs为静态压缩试验中的峰值强度。

（2）

式中：d1～d6均是筛孔的直径。

公式（1）的计算结果见表1。

分析表1可知，随着应变率增加，含黏结界面混凝土的强度动态提高因子呈现先线性增加，后趋于稳定的趋势。在低应变率的情况下，含黏结界面混凝土的变形速度较慢，这说明混凝土的内部结构有足够的时间来调整和适应应力的变化，因此，它的力学性能并没有得到充分发挥，在低应变率的情况下，强度动态提高因子的值相对较小。然而，随着应变率增加，混凝土的变形速度加快，其内部的微观结构和力学响应也会发生相应改变，这使混凝土的力学性能发挥得更好，从而使强度动态提高因子的值增加。这个过程也可以理解为混凝土在更高的应变率下，通过调整其内部结构，提高了其对应力的抵抗能力。然而，当应变率进一步增至一定程度时，混凝土的动态响应已经趋于饱和，即混凝土已经充分发挥了其力学性能，此时强度动态提高因子的值趋于稳定。这个现象表明，尽管应变率继续增加，但混凝土的力学性能并没有进一步提高，反而趋于稳定。因为在高应变率下，混凝土的内部结构已经达到了一种平衡状态，所以无法进一步调整来提高其力学性能。

公式（2）的计算结果见表2。

细度模数是评价混凝土骨料的一个重要参数，它主要受到材料的颗粒组成和粒径分布等因素的影响。然而应变率是描述材料变形速度的一个参数，它反映了材料在受力时的应变程度。虽然应变率对混凝土的力学性能有一定影响，但对细度模数的影响较小。因为细度模数主要受混凝土的物理性质和成分影响，而与应变率的关系不大。所以，在给定的应变率范围内，无论应变率如何变化，细度模数基本都稳定在1.5～1.75。这说明细度模数是一个相对稳定的参数。

动态峰值应变是衡量材料在动态加载条件下所能承受的最大应变程度的指标。表3为含黏结界面混凝土在受不同冲击加载速率下的动态峰值应变变化情况。

分析表3可知，含黏结界面混凝土的动态峰值应变与应变率呈正相关。然而，与静态压缩试验相比，SHPB冲击试验中的峰值应变明显减少。具体而言，当应变率为10s-1时，与静态压缩试验相比，含黏结界面混凝土的峰值应力降低了86.3%。这说明在冲击试验中，混凝土的应力承载能力明显降低，冲击载荷的高能量和短时间作用，导致混凝土无法充分适应和分散冲击能量，从而使其峰值应变明显减少。而当应变率增至45s-1时，与静态压缩试验相比，含黏结界面混凝土的峰值应力降低了9.8%。尽管应变率较高，但降低的幅度相对较小。这表明在较高的应变率下，混凝土的应力承载能力仍然能够保持相对稳定，虽然有一定程度降低，但降低幅度不如较低应变率下的明显。这种现象可以解释为，当应变率增加时，混凝土无法充分适应和分散冲击能量，导致部分能量转化为局部破坏和断裂，从而使峰值应变减少。尽管如此，混凝土仍能在一定程度上承受冲击载荷，使其峰值应力相对稳定，说明含黏结界面混凝土在动态加载下具有一定的抗冲击性能，但与静态加载相比，其整体破坏能力有所降低。

冲击韧性是指当材料受到冲击或冲击载荷时能够吸收能量并继续承受冲击载荷而不发生破坏的能力。根据SHPB冲击试验中含黏结界面混凝土的冲击韧性的变化可知，当应变率较低时，随着应变率增加，含黏结界面混凝土的冲击韧性提高。然而，当应变率达到一定值时，总韧性、破坏前的冲击韧性和破坏后的冲击韧性均出现逐渐降低的趋势。这是因为在较低的应变率下，材料有足够的时间进行塑性变形和能量吸收，所以能提高总韧性和冲击韧性。而在高应变率下，材料的变形速率增加，塑性变形的能力受到了限制，削弱了材料的吸能能力，使总韧性和冲击韧性降低。

3 模型验证

根据损伤力学理论中的等应变假设，在一维应力状态下，应力的分布可以用公式（3）表示。

σ=E（1-D）ε （3）

式中：σ为应力；E为弹性模量；D为损伤变量；ε为应变。

在Weibull分布的概率密度函数下损伤变量可以用公式（4）表示。

（4）

式中：n和k均为拟合参数。

根据公式（4），公式（3）可以转化为公式（5）。

（5）

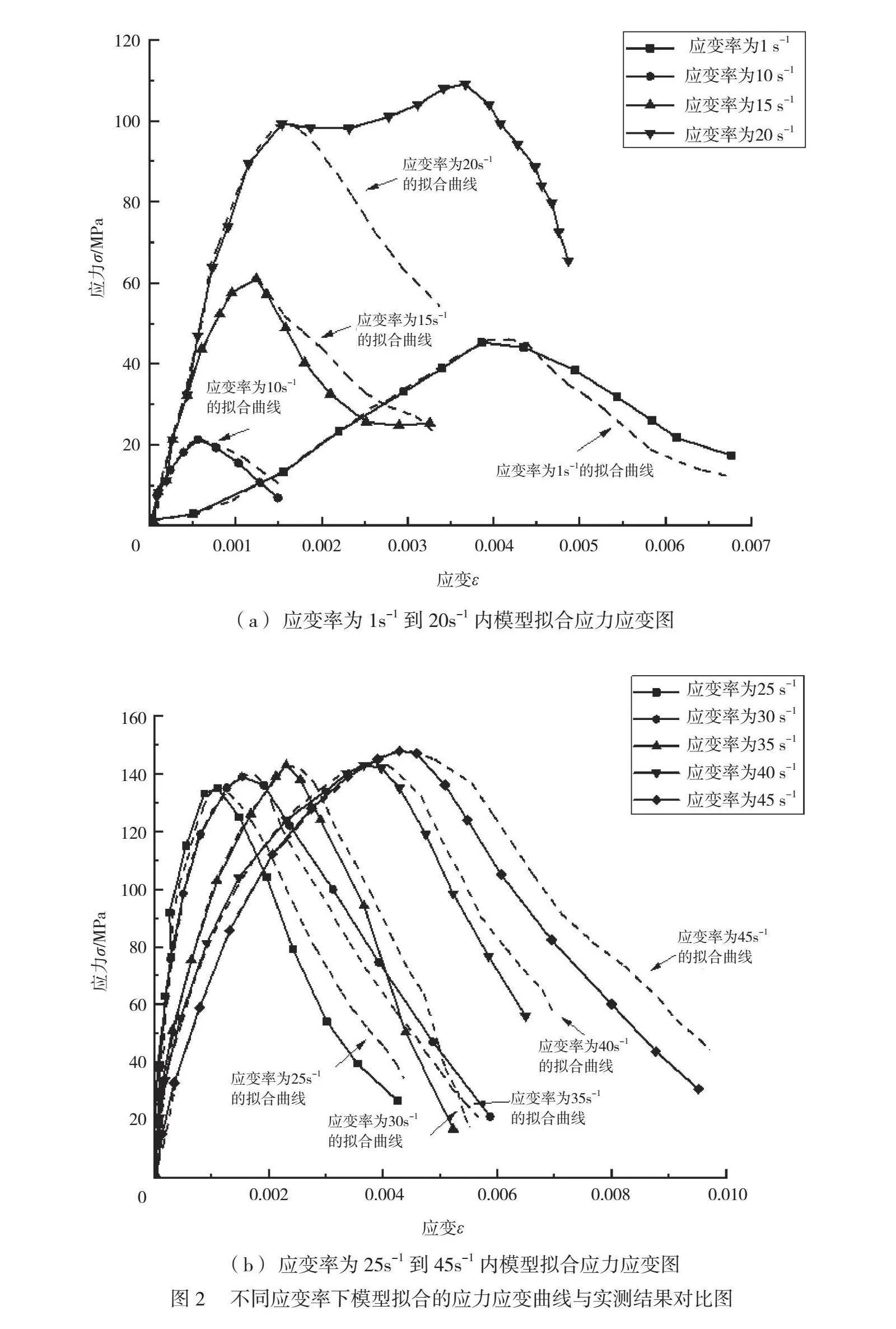
通过公式（5）拟合SHPB冲击试验中不同应变率下的应力应变数据，结果如图2所示。

根据图2可知，公式（5）在不同应变率下的拟合程度较好，特别是应力随着应变增加而增加的阶段，公式（5）的拟合值与预测值几乎一致，但是当应变超过屈服应变后，公式（5）的拟合值逐渐变差，可能是由于Weibull分布的本构模型是基于一些简化的假设，因此这些假设无法完全描述混凝土在复杂加载条件下的行为，导致模型在应力应变全曲线方面的适用性受限。

4 结论

本文通过静态压缩试验和SHPB冲击试验，对含黏结界面混凝土在不同应变率下的破坏与受力进行试验研究，并利用Weibull分布的本构模型对试验数据进行了拟合，得出以下主要结论。1）含黏结界面混凝土在不同应变率下的应力应变曲线表现出明显的动态硬化效应。2）含黏结界面混凝土在不同应变率下的强度动态提高因子呈现先增后趋于稳定的趋势，而细度模数则基本稳定在1.5～1.75。3）含黏结界面混凝土在不同应变率下的冲击韧性均呈现先增后减的过程。4）Weibull分布的本构模型能够较好地拟合含黏结界面混凝土在不同应变率下的应力-应变曲线，但是当应变超过屈服应变后，Weibull分布的本构模型仍然无法完全反映材料在复杂加载条件下的行为。

参考文献

[1]赵文，梁磊，张锋春，等.冲击荷载作用下混凝土的受力分析[J].东北大学学报（自然科学版），2008，29（5）：4.

[2]沈峰，章青，黄丹，等.冲击荷载作用下混凝土结构破坏过程的近场动力学模拟[J].工程力学，2012（增刊1）：12-15.

[3]许斌，曾翔.冲击荷载作用下钢筋混凝土梁性能试验研究[J].土木工程学报，2014，47（2）：12.

[4]雷光宇，党发宁，陈厚群.冲击荷载作用下混凝土破坏强度的确定及CT验证[J].地震工程与工程振动，2013，33（3）：7.