人工智能在多模态学习中跨学科知识整合研究

摘 要：本研究引入一种新的跨学科知识整合方法，即KIDDT（Knowledge Integration for Diverse Disciplinary Teams）算法，并通过一系列试验评估其在多模态学习环境中的性能。采用3种不同的模型，分别使用K-Means聚类算法、主成分分析和支持向量机、以及深度学习神经网络（CNN），对比它们的准确率和生成时间，深入研究了算法在不同条件下的表现。试验结果表明，在不同数据块数量和突变概念飘移影响下，3种模型展现出不同的性能特征。使用CNN的模型三在准确率方面表现出色，尤其在突变概念飘移的环境中更稳定，由于生成时间较长，因此在实际应用中需要在准确性和效率之间进行权衡。

关键词：人工智能；多模态数据；跨学科

中图分类号：G 202" " " " " 文献标志码：A

人工智能（AI）技术已经渗透到各个领域中。随着知识图谱和跨学科研究的兴起，如何在多模态学习环境中整合跨学科知识成为一个备受关注的课题。在这个背景下引用相关文献，更好地理解并探讨多模态学习环境中的跨学科知识整合。过去的研究已经在知识图谱的构建、学科教学知识构建和跨库知识整合等方面取得了一系列重要成果。曾晓玲等[1]研究了基于黄河资源整合共享的知识图谱，为资源整合方面提供了启示。刘冬萍等[2]在课堂切片与诊断方面的研究以及王素月等[3]对教师整合人工智能的学科教学知识建构的研究为后续提供了宝贵的经验，有一定参考价值。

1 知识整合

1.1 算法概述

KIDDT（Knowledge Integration and Dynamic-Teaching Algorithm for Domain Transfer）算法的核心思想是自适应学习和语义关联的融合。该算法构建1个多维知识空间来整合不同学科的知识。这个多维知识空间中的每个维度都对应一个特定的学科。用K来表示这个多维知识空间，其中Kij表示第i个学科和第j个知识维度的关联。其大小为m×n，其中m表示学科的数量，n表示知识的维度。

在自适应学习过程中，引入一个自适应学习矩阵W，其目的是在知识整合的过程中自动调整权重，使不同学科的知识能够得到合理整合。Wij的计算过程如公式（1）所示。

（1）

式中：Wij为自适应学习矩阵中的元素；i和j分别为学科的索引。Kik和 Kkj分别为学科i和学科j在知识空间中的向量表示的元素。求和符号表示对所有知识维度k进行求和。

公式（1）的核心思想是通过计算知识空间中不同学科之间的余弦相似度来更新权重。在更新过程中，相似度较高的学科之间的权重会得到提高，而相似度较低的学科之间的权重则会相应降低。这样，KIDDT算法就能够根据知识空间的动态变化自适应地调整权重，从而对知识进行有效整合。

1.2 多模态信息关联

在多模态学习环境中面对的不是单一类型的数据或信息，而是多种模态的混合体。将视觉、听觉和文字等多模态信息表示为向量V、A、T，它们分别对应视觉、听觉和文字学科的知识。为了进行信息关联，定义1个关联矩阵R，其目的是捕捉不同模态之间的语义关联。关联矩阵的更新过程如公式（2）所示。

（2）

式中：Rij为模态i和模态j之间的关联。tanh是一种常见的非线性激活函数。它能够更好地捕捉信息之间的复杂关系，通常用于神经网络中。TVA为视觉模态V与听觉模态A之间的交互。

通过内积运算，它捕捉了视觉信息和听觉信息之间的相关性。TAT为听觉模态A和文字模态T之间的交互。通过内积运算，它衡量了听觉信息和文字信息之间的关联程度。TTV为文字模态T和视觉模态V之间的交互。通过内积运算，它描述了文字信息和视觉信息之间的相关性。

在多模态学习中，各种信息之间的关系往往是非线性的，因此引入非线性映射是必要的。

在这类领域的相关研究中，更多研究也探讨了基于知识库的知识整合与知识管理。卢利农等讨论了知识库整合与知识指纹设计[4]。张喜征等对碎片化知识整合的知识图谱构建进行分析[5]。基于此，在多模态学习环境中，理解和整合不同模态之间的关联是至关重要的，而KIDDT算法提供了一个有效的工具来实现该目标。

1.3 复杂性分析

时间复杂度衡量的是算法运行所需的时间与输入规模之间的关系。在KIDDT算法中，学科数量、知识维度和模态数量都会影响算法的运行时间。KIDDT 算法的时间复杂度如公式（3）所示。

OTC=O（mn2+pn2）" " " " " " " " （3）

式中： OTC为时间复杂度；O为复杂度；m为学科数量；n为知识维度；p为模态数量。这个公式涵盖了算法中的不同计算部分，包括自适应学习矩阵的更新、多模态信息的关联等。从公式（3）可以看出，算法的时间复杂度与学科数量、知识维度和模态数量的平方成正比。说明随着这些参数增加，算法的运行时间也会相应增加。空间复杂度则衡量了算法所需存储空间的大小。在KIDDT算法中，需要存储自适应学习矩阵、关联矩阵以及不同模态的向量表示等信息。空间复杂度如公式（4）所示。

OSC=O（mn+pn） （4）

式中：OSC为时间复杂度；m为学科数量；n为知识维度；p为模态数量。

公式（4）包括了自适应学习矩阵、关联矩阵以及不同模态向量表示所需的存储空间。空间复杂度与学科数量、知识维度和模态数量的线性关系成正比。这类知识管理体系对实践应用相关知识来说有重要价值，例如李占雷等对知识管理能力的差异性和企业商业模式创新影响进行分析[6]。基于此，相应复杂度分析结果也说明随着这些参数增加，算法所需的存储空间也会相应增加。

2 测试结果

2.1 测试用模型

为了评估KIDDT算法在多模态学习环境中的性能，在试验环境中对其进行测试。为了全面了解多模态数据经过进一步降维过程的差别，采用3种不同的模型进行测试。模型一基于K-Means聚类算法，它是一种无监督学习方法，通过迭代寻找数据的簇中心，将数据点划分到不同的簇。这种方法在知识整合的初步阶段非常有效，能够帮助人们了解数据的内在结构和模式。通过K-Means聚类，可以将多模态数据划分为若干个簇，每个簇代表一个知识领域或主题。模型二结合了主成分分析和支持向量机的方法。主成分分析（PCA）是一种降维技术，它通过线性变换将原始特征转换为新的特征集合，新特征按照方差从大到小的顺序排列。这样做的目的是提取数据的主要特征，去除冗余和无关的信息，使数据更加简洁和易于处理。而支持向量机（SVM）则是一种分类算法，用于识别数据中的模式和分类任务。通过结合PCA和SVM，模型二能够利用多模态信息，考虑数据的降维处理，进行有效分类和模式识别。模型三采用深度学习神经网络，特别是卷积神经网络（CNN）。深度学习算法在图像识别、语音识别和自然语言处理等领域广泛应用。 因为CNN能够自动学习数据的特征表示，所以特别适合处理图像等多模态数据。通过训练，CNN可以识别出图像中的边缘、纹理等低级特征以及更高级别的抽象特征。模型三利用深度学习网络实现了更复杂的语义关联，能够更准确地整合多模态知识。

2.2 准确率对比

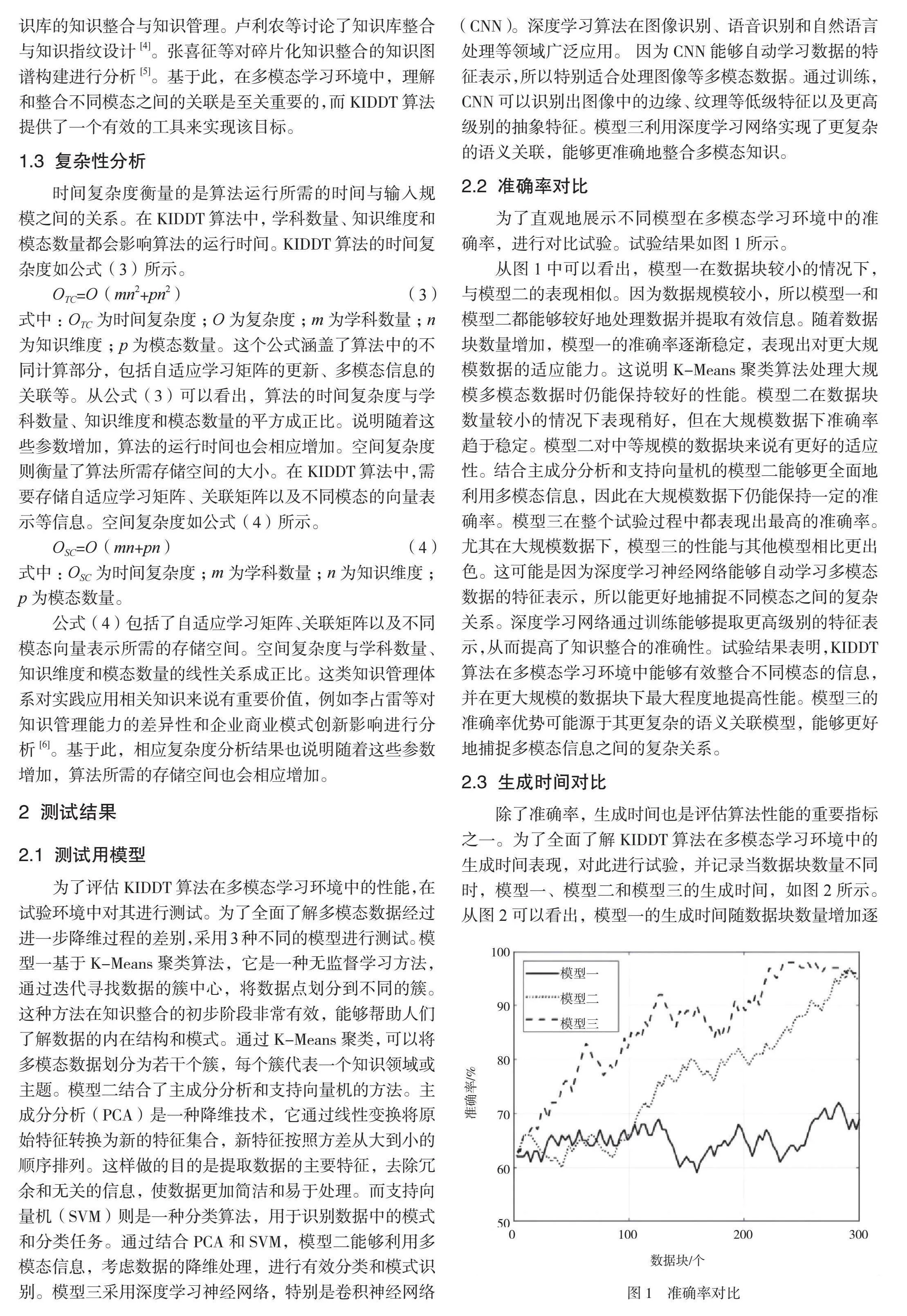
为了直观地展示不同模型在多模态学习环境中的准确率，进行对比试验。试验结果如图1所示。

从图1中可以看出，模型一在数据块较小的情况下，与模型二的表现相似。因为数据规模较小，所以模型一和模型二都能够较好地处理数据并提取有效信息。随着数据块数量增加，模型一的准确率逐渐稳定，表现出对更大规模数据的适应能力。这说明K-Means聚类算法处理大规模多模态数据时仍能保持较好的性能。模型二在数据块数量较小的情况下表现稍好，但在大规模数据下准确率趋于稳定。模型二对中等规模的数据块来说有更好的适应性。结合主成分分析和支持向量机的模型二能够更全面地利用多模态信息，因此在大规模数据下仍能保持一定的准确率。模型三在整个试验过程中都表现出最高的准确率。尤其在大规模数据下，模型三的性能与其他模型相比更出色。这可能是因为深度学习神经网络能够自动学习多模态数据的特征表示，所以能更好地捕捉不同模态之间的复杂关系。深度学习网络通过训练能够提取更高级别的特征表示，从而提高了知识整合的准确性。试验结果表明，KIDDT算法在多模态学习环境中能够有效整合不同模态的信息，并在更大规模的数据块下最大程度地提高性能。模型三的准确率优势可能源于其更复杂的语义关联模型，能够更好地捕捉多模态信息之间的复杂关系。

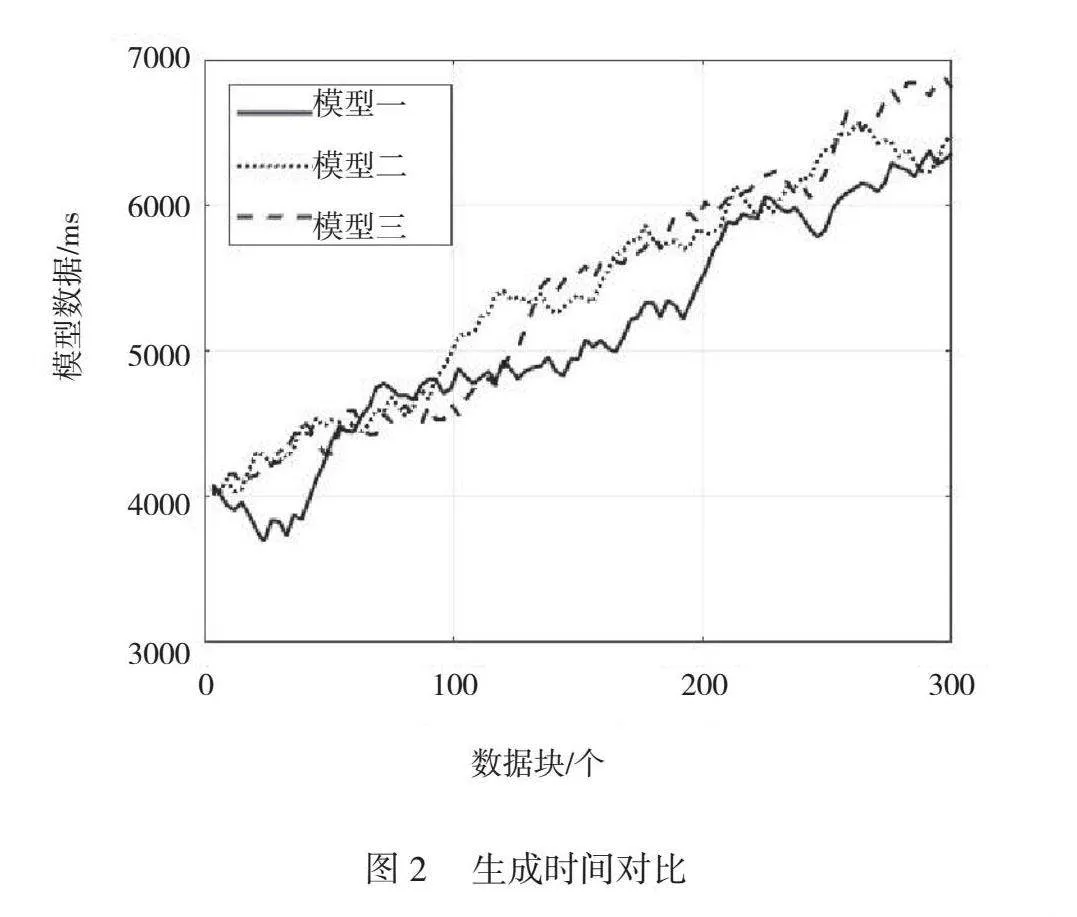
2.3 生成时间对比

除了准确率，生成时间也是评估算法性能的重要指标之一。为了全面了解KIDDT算法在多模态学习环境中的生成时间表现，对此进行试验，并记录当数据块数量不同时，模型一、模型二和模型三的生成时间，如图2所示。从图2可以看出，模型一的生成时间随数据块数量增加逐渐增加。与模型二和模型三相比，模型一在所有数据块数量下的生成时间都较短。这可能是因为模型一是一种相对简单和高效的算法，采用K-Means聚类算法对数据块的生成速度较快。模型二在初始数据块数量下的生成时间较快。随着数据块数量增加，生成时间逐渐延长，且趋势比模型一更显著。因为模型二结合了主成分分析和支持向量机的方法，所以需要进行更多计算和数据处理，生成时间相对较长。模型三在所有数据块数量下都展现出最长的生成时间。在较大规模数据下，其生成时间的增长趋势也更明显。因为模型三采用深度学习神经网络，需要进行复杂的特征学习和模式识别，所以增加了计算成本，延长生成时间。从生成时间的结果可以看出，模型三在准确率上表现出了显著的优势，但同时生成时间也更长。在实际应用中，须根据具体需求来权衡模型的准确性和生成时间。在某些对实时性要求较高的场景中，模型一或模型二可能更合适；而在对知识整合精度要求较高的情况下，模型三则能够提供更好的性能。

2.4 考虑突变概念飘移的准确率对比

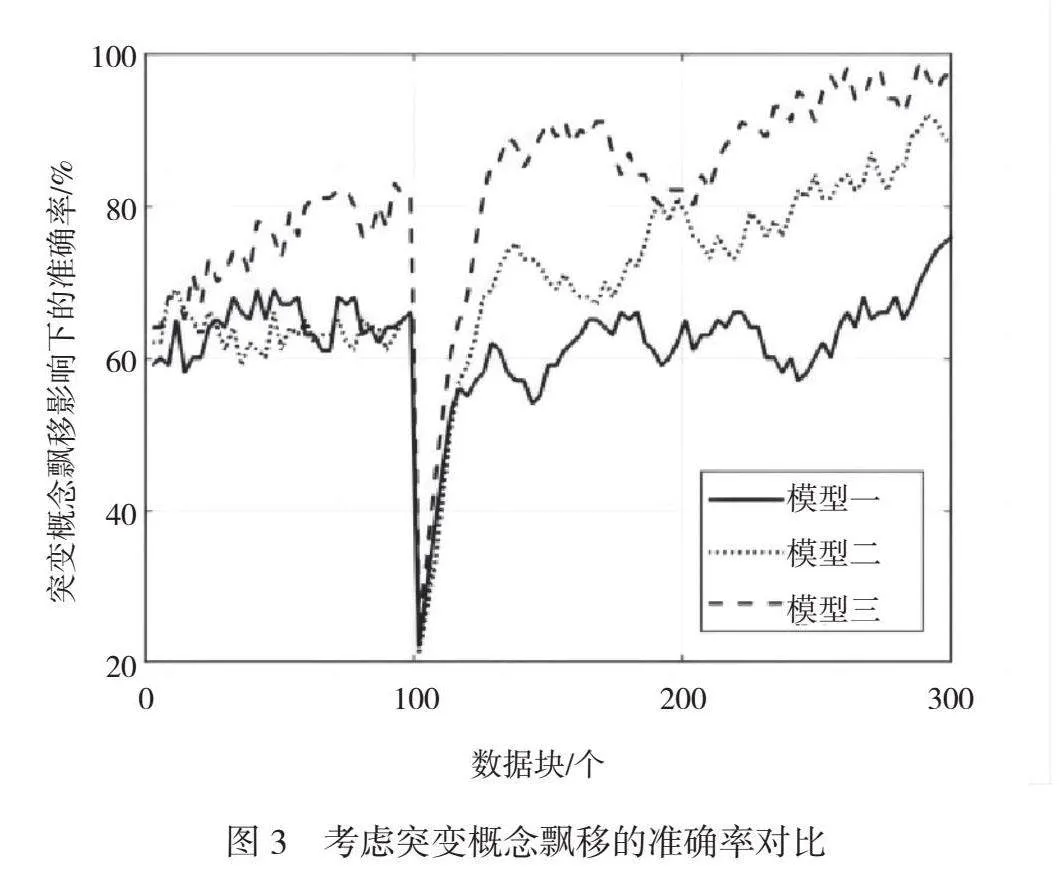
突变概念飘移是指当学习系统中的数据分布发生明显变化时的现象。在学习过程中，如果训练数据的统计特性发生显著改变，那么学习模型可能会失效，导致性能下降。这种变化是由外部因素、数据源变更和环境演变等因素引起的，模型在新的数据分布下难以适应。由于市场需求变化、新技术的引入或环境变迁，因此学习系统可能面临各种概念的快速变化。为了保证模型在不同情境下的稳健性，测试突变概念飘移是至关重要的。同时，对突变概念飘移进行测试有助于增强学习系统的鲁棒性。鲁棒的系统能够处理未知的数据变化，从而更好地适应新的任务和环境。本文在引入突变概念飘移的基础上进一步进行测试，结果如图3所示。

在突变概念飘移的影响下，模型一的准确率整体呈上升趋势。尽管初始准确率相对较低，但是随着数据块数量增加，模型逐渐适应了突变概念飘移。模型二在突变概念飘移下的准确率相对较高，但是当数据块数量增加时，准确率波动较大。模型二可能对突变概念飘移的适应性有一定局限。模型三在所有数据块数量下的准确率均为最高。尤其在突变概念飘移的情况下，与其他模型相比，模型三表现更稳定。试验结果表明，KIDDT算法在突变概念飘移影响下仍能有效整合不同模态的信息，并在更大规模数据块下取得更好的性能。模型三在突变概念飘移的环境中的稳定性更强，说明其对概念变化的适应性更好。

3 结论

本研究引入KIDDT算法，成功探索了在多模态学习环境中跨学科知识整合的新途径。试验证明，利用该算法能够更好地整合不同学科领域的知识，为学习者提供更丰富、全面的学习体验。在教育领域，为未来人工智能在多领域应用中的发展提供有益的经验和思路。本研究的成果能够促进跨学科研究的合作，推动人工智能技术在教育和其他领域的创新应用。未来将继续改进算法，提高对突变概念飘移的适应性，以更好地满足实际应用的需求。这项研究为跨学科合作、人工智能教育和知识整合领域的发展提供有益的指导。

参考文献

[1]曾晓玲，张弓.基于黄河资源整合共享的知识图谱研究和应用[J].人民黄河，2021，43（增刊2）：282-284.

[2]刘冬萍，张海，崔宇路，等.课堂切片与诊断：基于TPACK“六边模型”的图谱分析新视角[J].远程教育杂志，2021，39（2）：95-102.

[3]王素月，罗生全.教师整合人工智能的学科教学知识建构[J].湖南师范大学教育科学学报，2021，20（4）：68-74.

[4]卢利农，祝忠明，张旺强，等.基于Lingo3G聚类算法的机构知识库跨库知识整合与知识指纹服务实现[J].数据分析与知识发现，2021，5（5）：127-132.

[5]张喜征，罗文，蔡月月.基于知识图谱的用户生成内容平台中碎片化知识整合研究[J].科技管理研究，2019，39（5）：159-165.

[6]李占雷，霍帆帆，霍朝光.商业模式创新男女有别？——基于知识管理视角[J].华东经济管理，2017，31（10）：128-135.