基于改进信息量模型的地质灾害易发性评价

摘 要：信息量模型在地质灾害评价中具有重要的应用价值，但是在信息量计算过程中，未能考虑单因素对评价目标的影响程度。研究过程分别运用层次分析法和逻辑回归模型构建了层次分析法-信息量模型、信息量耦合逻辑回归模型，在该过程中引入了权重的概念，提高了模型的评价精度。将某县域地区作为评价对象，分别运用3种模型分析地质灾害易发性，结果显示，信息量耦合逻辑回归模型的评价效果最佳，层次分析法-信息量模型次之，验证了改进方法的有效性。

关键词：改进信息量模型；地质灾害；易发性评价

中图分类号：P 694" " 文献标志码：A

地质灾害的发生具有特定的诱发因素和孕育条件，将高程、坡度、降雨量、工程地质岩组等作为评价因子，利用信息量模型可以计算各评价单元的地质灾害易发性。但评价因子的影响力存在差异，因此当计算单元内的总信息量时，应该区分各因子的权重，逻辑回归模型和层次分析法可用于计算评价因子的权重，因此在其基础上建立改进的信息量模型。

1 信息量模型概述

地质灾害的发生通常包括高程、坡向、坡度、工程地质、断裂构造等信息。信息量模型能够同时考虑多种因素相互叠加后的影响，成为预测地质灾害易发性的重要理论方法[1]。国内从1985年起，将该理论应用于滑坡灾害的评估，构建了相应的数学模型，如公式（1）所示。

（1）

式中：xi（i=1，2，...，n）为引起地质灾害的各种因素；y为灾害事件；I（y，x1，x2，...，xn）为各致灾因素组合的信息量；在因素组合（x1，x2，...，xn）的影响下，P（y|x1，x2，...，xn）为灾害事件y的发生概率；P（y）为归一化处理区域发生滑坡的概率[2]。可通过单因素信息量的加和来求解多因素组合的信息量，单因素信息量的计算方法如公式（2）所示。

（2）

式中：xi为第i种致灾因素；P（y|xi）为致灾因素作用下，灾害y的发生概率；Ii（y，xi）为致灾因素xi对应的信息量。

在实际应用中，需要明确概率的计算方法，提高信息量理论模型的可操作性。在单因素影响下，地质灾害发生时的信息量计算方法可改写为公式（3）。

（3）

式中：S为研究区域内评价单元的总数；Si为含有致灾因素xi的单元数；N为研究区域内具有灾害分布的单元总数；Ni为含有致灾因素xi的单元数量。

每个评价单元内通常具有多种致灾因素，其信息量值是多种因素共同作用的结果。将评价单元总的信息量值记为Itotal，则Itotal的计算过程如公式（4）所示。

（4）

式中：n为参评因子数。

2 改进信息量模型

2.1 基于层次分析法的改进信息量模型

2.1.1 层次分析法的基本原理

层次分析法是一种处理复杂问题的量化决策方法，其实施步骤为建立层次结构→构造判断矩阵→计算同级指标的权重→进行一致性检验→若通过一致性检验，则结束→如果未通过检验，就重新回到第二步[3]。在层次分析法中，层次结构大多分为3层，包括目标层、准则层和指标层，每个层次均可构成一个判断矩阵。将判断矩阵记为A=（aij）m×m，aij为矩阵中的任意元素，i、j分别为矩阵中的行和列，m为矩阵的阶数。当构造判断矩阵时，需要通过1-9标度法两两对比同一层次各指标的重要性，取值方法见表1。计算判断矩阵A的特征向量，即可得到对应指标的权重。

2.1.2 层次分析法-信息量模型构建

在信息量模型中，求出各致灾因素的信息值后，再进行加和，即可得到总的信息量值Itotal[4]。但对地质灾害易发性评价来说，各致灾因素的影响程度存在差异，此时可通过层次分析法计算权重系数，计算Itotal时加入权重考量，计算过程如公式（5）所示。

（5）

式中：Wi为致灾因素i对灾害易发性的影响权重，该参数需要通过层次分析来确定。

2.2 基于逻辑回归的改进信息量模型

2.2.1 逻辑回归的基本原理

逻辑回归用于评价两种或多种变量间的相互依赖性，本质上是一种线性回归模型，其中涵盖因变量和自变量。将地质灾害发生与否作为因变量，1表示发生，0表示不发生，利用逻辑回归模型描述该问题，可得到公式（6）。

（6）

式中：β0～βi为逻辑回归的系数；X0～Xi为自变量；P为单个评价单元内地质灾害的发生概率，如果P的计算结果越大，就说明该评价单元越容易发生地质灾害，P的计算方法如下。P=（eβ0+β1X1+β2X2+β3X3+...+βiXi）/（1+eβ0+β1X1+β2X2+β3X3+...+βiXi），其中e为自然常数。

2.2.2 信息量耦合逻辑回归模型

利用传统的信息量模型计算各因子的信息量值后，将致灾因素作为自变量，地质灾害是否发生作为因变量。利用逻辑回归模型分析自变量的信息量值与因变量间的关系，进而形成信息量耦合逻辑回归模型，该模型可用于预测地质灾害易发性[5]。

3 基于改进信息量模型的地质灾害易发性评价

研究过程分别运用传统的信息量模型、层次分析法-信息量模型和信息量耦合逻辑回归模型对地质灾害易发性进行评价，根据预测结果对比3种模型的效果。

3.1 待评价地区和评价单元划分

3.1.1 待评价地区概况

某县长度约97km，宽度约58km，辖区总面积约1729.889km2，包括98个行政村，人口数量为11.93万。所在地区涵盖2条高速路、2条省道、6条县道。该县位于武夷山东麓，地形包括山地、丘陵、小盆地，海拔为200～800m，绝大部分地区的海拔为300～500m。从地质构造来看，该地区沿东西向、北东向、北西向、北-北东向分布若干断裂带。根据历年的地质灾害数据，该县地质灾害类型主要为崩塌和滑坡，现有的统计数据分别为65处和48处，占比分别为57.52%和42.48%。

3.1.2 划分评价单元

划分评价单元是实施信息量模型的关键步骤，常用的划分方式包括行政单元划分、地貌单元划分以及规划格栅单元。此次研究中运用ArcGIS软件，对待评价地区进行规划格栅单元划分，格栅为正方形，其尺寸的计算过程如公式（7）所示。

GS=7.49+0.0006S'-2.0×10-9S'2+2.9×10-15S'3" （7）

式中：Gs为适宜网格的边长数值；S'为原始等高线数据精度的分母。评价过程使用的等高线数据采用1∶10000的比例尺，因此式中S'的取值为10000，将其代入公式（7），可计算网格边长为13.2929m。研究区域的数字高程模型数据的规格为10.0m，与计算所得的Gs数据存在一定的差异，为便于后续的计算，将网格统一设计为10m×10m，按照这一标准进行网格划分，将该县的评价区域划分为172.9889万个格栅单元。

3.2 基于信息量模型的地质灾害易发性评价

3.2.1 单因子信息量计算

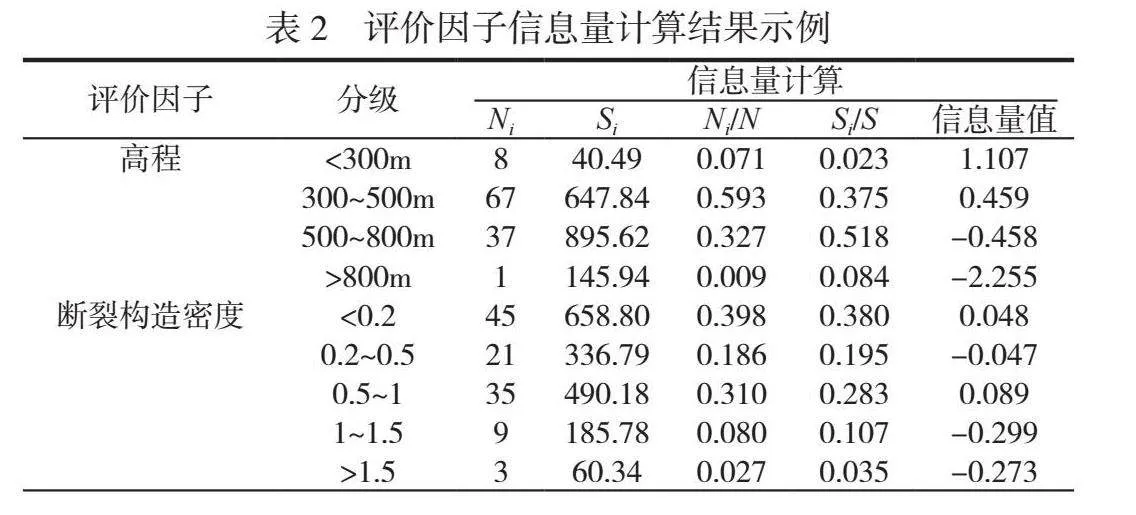
根据信息量模型的实现原理，将致灾评价因子设计为8个，包括高程、坡度、坡向、路网密度、工程地质岩组、断裂构造密度、降雨量以及植被覆盖度。对评价因子进行量化分级，并且得出单因子信息量计算的相关参数，结果见表2。参数S的取值为县域面积（1729.889），参数N的取值为113。坡度评价因子划分为以下分级指标，分别为lt;10°、10°～20°、20°～30°、30°～40°、40°～50°和gt;50°。坡向评价因子划分为9个分级指标，分别为平面（0°）、北（337.5°～22.5°）、北东（22.5°～67.5°）、东（67.5°～112.5°）、南东（112.5°～157.5°）、南（157.5°～202.5°）、南西（202.5°～247.5°）、西（247.5°～292.5°）、北西（292.5°～337.5°）。植被覆盖度评价因子划分为5个分级指标，分别为lt;0.3、0.3～0.5、0.5～0.7、0.7～0.8和gt;0.8。降雨量评价因子划分为8个分级指标，分别为lt;1650mm、1650～1700mm、1700～1750mm、1750～1800mm、1800～1850mm、1850～1900mm、1900～1950mm和gt;1950mm。

3.2.2 地质灾害易发性分区计算结果

得出单因子的信息量值后，利用软件工具对单元上的多个单因子进行叠加分析和计算，求得单元上的信息量总值，根据信息量值区分地质灾害易发区，结果见表3。

3.3 基于层次分析法-信息量模型的地质灾害易发性评价

3.3.1 基于层次分析法的评价因子权重计算

将地质灾害易发性评价问题划分为3个层次结构，目标层为灾害易发性评价（A），准则层为孕灾条件（B1）和诱发条件（B2），B1的指标层对应6个评价因子，包括高程、坡向、坡度等，B2的指标层为路网密度、降雨量，运用层次分析法计算指标层的权重，结果见表4。

3.3.2 基于层次分析法-信息量模型的易发性评价结果

在得出评价因子的权重后，按照公式（5）计算加权信息量，再运用ArcGIS软件计算各单元上的信息量总值，易发区评价的结果见表5。

3.4 基于信息量耦合逻辑回归模型的地质灾害易发性评价

3.4.1 致灾评价因子共线性分析

在逻辑回归模型中，共线性会降低模型计算的准确性，因此要避免各因素间存在共线性问题。可通过方差膨胀因子（VIF）和容忍度（TOL）判断各因子是否具有共线性。判断标准为VIFgt;10或者TOLlt;0.1。经过计算，8个评价因子的VIF的值在1.022～1.396，TOL数值在0.684～0.978，说明8个因子不具有共线性，满足要求。

3.4.2 基于信息量耦合逻辑回归模型的易发性评价结果

评价区域内具有113个灾害点，再借助软件工具生成同等数量的非灾害点，共形成266个样本点，计算所有样本点的信息量，将其导入SPSS软件，进行二元逻辑回归分析，进而求出8个致灾因子的回归系数，按照表4中C1～C8的顺序，对应的回归系数分别为0.264、0.143、0.072、0.031、0.273、0.109、0.231、0.132。根据公式（6）的原理计算各单元的灾害发生概率，得到易发性评价结果，见表6。

3.5 3种评价模型的效果对比

在效果评价中，引入评价指标地质灾害相对百分比（HAR），计算方法为HAR=POHN/POA，其中POHN、POA分别为分级面积中地质灾害发育个数在地质灾害总数中的百分比、分级面积和总面积的百分比。3种模型的HAR计算结果见表7。从中可知，信息量耦合逻辑回归模型计算的极高易发区和高易发区占比最大，其次为层次分析法-信息量模型，最后为信息量模型。说明在地质灾害易发性评价中，3种模型的效果排序为信息量耦合逻辑回归模型gt;层次分析法-信息量模型gt;信息量模型。

3.6 地质灾害易发生性总结

通过分析地质灾害的易发生性可以指导相关地区和部门技术采取应对措施，减少地质灾害导致的生命财产损失。通过上文分析可知，影响地质灾害的因素较多，越多的叠加因子能够提高地质灾害易发生评价结果精确度，不过当叠加因子的数量达到一定程度，其评价精确度也达到最高，之后不会出现精度明显降低或者提高的情况。在不同区域，地质灾害发生的可能性、影响因素均存在一定差异，相关评价人员需要对每个因素进行计算和控制，通过单因子信息量和曲线组合模型等措施明确地质灾害易发生的等级，得到地质灾害易发生评价结果，进而采取应对措施。地质灾害易发生性评价对社会有深远的意义，本文对信息量模型进行分析优化，希望可以为今后地质灾害的预测和应对提供支持。

4 结语

综上所述，以信息量模型为基础，借助层次分析法或者逻辑回归模型，在信息量计算中增加对评价因子的权重分配，由此可提高信息量的精确性和客观性。研究过程建立了两种改进的信息量模型，分别为层次分析法-信息量模型和信息量耦合逻辑回归模型。在某县域地区的地质灾害易发性评价中，这两种模型的效果均优于传统的信息量模型。

参考文献

[1]张文俊，何毛，郭德岭.基于改进的ArcGIS对石台县地质灾害易发性评价探讨[J].安徽地质，2023，33（1）：65-69，74.

[2]林幸俤.基于信息量法罗源县地质灾害易发性评价[J].能源与环境，2023（3）：2-6，10.

[3]沈石凯，张宏亮，闫家倩.河北省赤城县地质灾害易发性评价[J].地质论评，2023，69（增刊1）：487-488.

[4]李光辉，铁永波.基于信息量模型的综合地质灾害易发性建模方法对比研究[J].灾害学，2023，38（3）：212-221.

[5]范希飞，赵叶江，杨丽君.基于信息量模型的贵州六枝特区地质灾害易发性评价[J].工程技术研究，2023，8（6）：20-22.