智能运维中多维监测指标异常定位算法及试验研究

摘 要：智能运维系统涉及多种维度的监测指标，系统的重要功能是异常信息检测和原因自动化分析。本研究基于变分循环网络建立了异常信息时序定位算法，利用蒙特卡洛树搜索（Monte Carlo Tree Search，MCTS）设计针对多维因素的根因分析优化方法。利用系统实际监测数据训练算法模型，并对其性能进行检验。结果显示，与对照组相比，设计算法在精确率、召回率等方面具有优势。

关键词：智能运维；多维监测指标；异常定位算法；性能试验

中图分类号：TP 31" " " " " " " " " " " " " " 文献标志码：A

智能运维系统中的异常信息发生在监测时段内，但是监测模型对时间与异常之间的关联性反映不足。构建一种能够识别异常现象以及对应发生时刻的算法模型具有突出的实践价值。同时，多维监测指标对异常信息的影响程度存在主次之分，算法模型应该具备分析根本原因的功能。

1 基于变分循环网络的异常定位算法

1.1 异常定位算法的实施流程

智能运维系统中存在多种维度的监测指标，当部分指标在监测时间内出现异常时，要求算法工具能够在相关的时间序列内检测出异常时刻。假设时刻t为监测时序中的一个时间节点，数据集{xt-N，…，xt-1，xt}为时刻t之前的历史监测数据。基于变分循环网络（Variational Recurrent Neural Network，VRNN）的异常定位算法可用于检测异常时刻，其实施流程为利用最小化损失函数训练多维监测指标数据，形成异常定位模型。计算模型重建概率，判断重建概率是否大于设定的阈值，当判断结果为大于时说明数据异常。

1.2 基于VRNN网络的异常定位算法建模

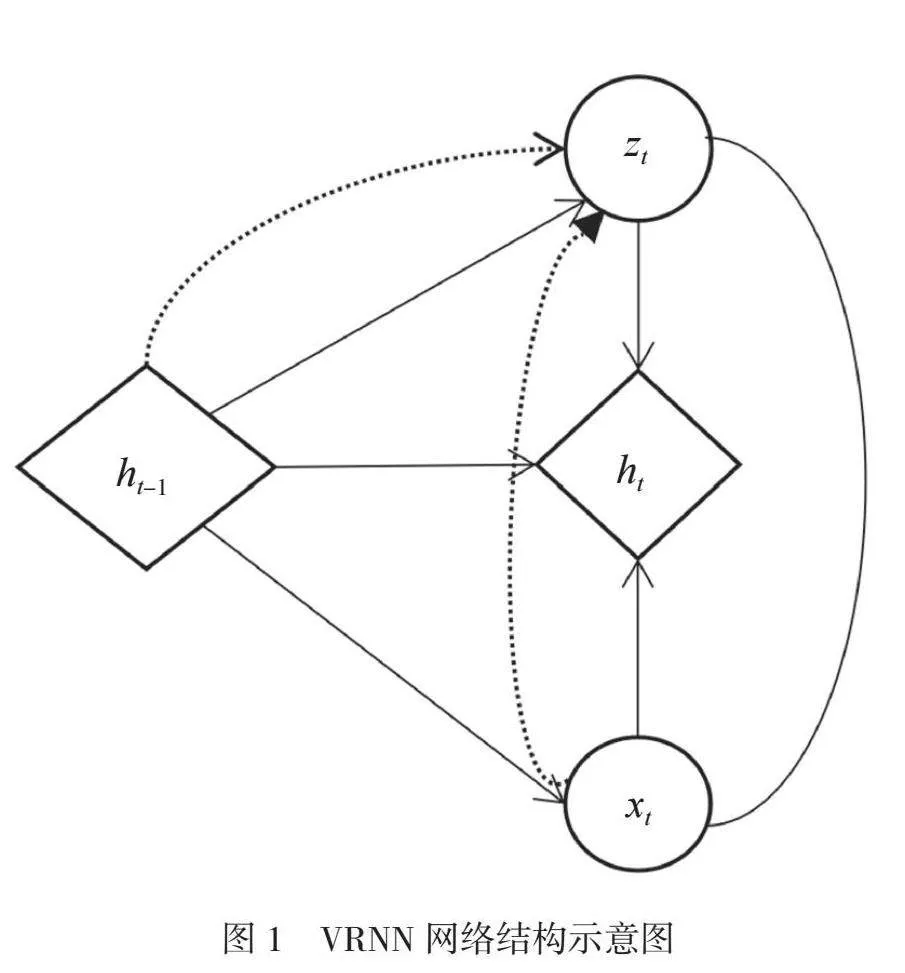
在异常检测中，变分自编码器（VAE）的使用十分广泛，但是以VAE为基础的检测方法并没有考虑时间序列内时间的相关性，而VRNN网络以VAE和长短期记忆（LSTM）网络为基础，VAE网络模块分布在每个时刻t上，长短期记忆网络的状态变量（记为ht-1）是VAE网络模块在时刻t的重要条件。在此基础上，VRNN网络模型能够反映监测数据的时序特征，进而定位异常数据对应的时间点，其网络结构如图1所示。其中，xt和zt分别为VAE模型在时刻t的输入变量和隐藏变量[1]。xt为矢量数据，如果以智能运维系统中的数据为标量，就需要对其进行矢量化表示，可采用滑动窗口技术实现。

VAE是VRNN的重要基础，因此VRNN中也存在隐蔽变量z，其先验分布参数的数学表达如公式（1）所示。

φtprior（ht-1）=zt～N（μztprior，（σztprior）2I），[μztprior，σztprior] （1）

式中：zt为隐藏变量z随时间的先验分布；μztprior，σztprior为zt中的参数，分别为该分布的均值和标准差；函数φtprior为神经网络，其输入参数为ht-1；I为指示策略；N为采样集。

该先验分布表达式在智能运维监测数据和时间序列之间建立了关联。从公式（1）可知，φtprior主要取决于2个参数。将ht-1的非线性映射结果记为h't-1，其运算过程如公式（2）所示。

h't-1=ReLU（linear（ht-1）） （2）

式中：linear（）、ReLU（）分别为线性变换函数、一种非线性激活函数；μztprior，σztprior2个参数的计算方法均与h't-1有统计学意义，具体计算过程如公式（3）、公式（4）所示。

μztprior=linear（h't-1） （3）

μztprior=Softplus（linear（h't-1）） （4）

式中：Softplus为另一种非线性激活函数。求解标准差可通过该激活函数和ε（服从标准正态分布的变量）导出σx和σz。

VRNN网络能够重新构建xt，重构过程与隐藏变量在前一时刻的状态变量以及其随时间的先验分布有统计学意义，其解码过程与VAE网络模块的解码原理基本一致。以高斯分布描述经过重建的xt，采集隐藏变量的近似后验分布样本，通过 VRNN 解码网络的映射变换获取xt重建时的参数分布，重构过程如公式（5）所示。

xt|zt～N（μσ2I），[μ，σ]=φτdec（φτz（zt），ht-1） （5）

式中：当以高斯分布表示重构的xt时，需要引入对应的均值参数和标准差参数μ、σ；φτz（zt）为神经网络的特征提取阶段，用于从隐藏变量中提取有效的特征点；φτdec（）为神经网络模型的解码阶段，以重构的xt为数据，经过解码后生成参数分布。Softplus、ReLU这2种激活函数可构建出神经网络特征提取阶段和解码阶段的函数表达式[2]。VRNN网络模型在迭代的过程中需要更新隐藏状态，参数ht也随之变化，ht与ht-1之间的关系如公式（6）所示。

ht=fθ（φτx（xt），φτz（zt），ht-1） （6）

式中：fθ为LSTM网络的运行机制。

通过以上分析可知，VRNN网络兼顾了长短期记忆网络的时序特征和变分自编码器的隐藏变量，形成了具备时序特征的建模能力。

2 优化根因分析算法

在智能运维系统的多维指标监测中，除了定位异常指标及其发生的时间点，还需在此基础上进一步分析异常的原因，根因分析算法用于确定系统运维数据异常的根本原因。传统的根因分析算法采用MCTS原理，但是该算法在实际使用中存在一定的局限性，因此本研究以该算法为基础，建立了一种优化的根因分析算法，实现过程如下。

2.1 定义算法中的符号

智能运维系统的监测指标通常具有多个维度，即使确定了指标异常的具体时间点，但是各属性在异常现象中的作用有所差异，问题也无法解决。因此只有确定根因属性的组合，才能为异常问题的解决创造条件[3]。智能运维系统的监测数据由事件、时间戳以及属性值组成。事件包括多个属性，例如所在省份（记为P）、通信频道（记为C）、数据中心（记为D）以及运行商类型（记为I）。1个事件记为E（P，I，D，C），示例为（北京，电信，DC1，Channel3）。时间戳为系统检测出的事件发生的具体时间点。将根因分析算法中的异常属性组合记为e=（p，i，d，c），其中的4个属性为各自对应属性集中的1个元素。将所有属性组合e组成1个集合，将该集合记为LEAF，元素e在时间尺度下的实际值记为v（e），其对应值记为Value。

2.2 计算潜在分数

为了以形象化的方式表示多维监测指标，在分析过程中引入数据立方体（Data Cube）模型，其作用为支持多维度数据查询。根因集合中存在多个元素，其中任一元素的变化都会在数据立方体中产生影响，使后者发生一定程度的变化。

元素e是否属于集合LEAF的判断条件为e中是否存在通配符*，如果存在，则e不属于LEAF。将元素e在数据立方体中的子代元素记为e'，而元素e'i属于子代元素集合，记为e'i∈Desc'（e）[4]。当元素e发生变化时，将其变化量记为h（e），如公式（7）所示。

h（e）=f（e）-v（e） （7）

式中：f（e）为对元素e的预测值，可将元素e相应历史数据的均值赋值给f（e）；v（e）为智能运维监控系统在数据立方体下的实测结果；作为e的子代元素，ei'的预测值为f（ei'），其在元素e中占有一定的比例，该比例关系记为a（ei'），其计算过程如公式（8）所示。

（8）

但是需要注意，在不同维度拆分下元素e存在很多可能性，例如当e'=（p1，i1，d1），则e有可能是（p1，i1，*）、（p1，*，d1）或者（*，i1，d1）。因此，当对不同维度、不同集合的某一元素进行推导时，得到的a（ei）也存在差异。

潜在分数的计算阐明了根因集合中的元素对根因分析的整体影响程度。该计算方法对确定根因集合中的元素具有重要的作用，对比元素的潜在分数计算结果与实际观测值f（ei'），2种数值越接近，相应的集合成为根因集合的可能性越大[5]。

潜在分数的计算结果在0～1，当2个潜在的根因集合中均存在多个元素时，要综合计算集合的潜在分数，此时引入参数解释力（记为EP），其计算过程如公式（9）所示。

（9）

式中：f（ei）为根因集合中任一元素ei的预测值；v（ei）为f（ei）对应的智能运维系统实测值；f（total）为集合中所有元素预测值之和；v（total）为集合中所有元素观测值之和。可通过公式（9）对比不同根因集合的解释力EP值，从而确定最优的根因集合。

2.3 算法优化

将数据立方体记为B，根因分析算法的功能是从B中搜索潜在分数最大的子集。B对应的事件集记为E（B），其中存在n个元素，那么算法需要搜索2n-1次。显然，随着元素数量n越来越大，算法的搜索次数将快速增加，会造成极大的搜索负担。此处以MCTS原理为基础，构建优化的根因分析算法，目标位缩小搜索空间，减少负担。

在MCTS算法中，将搜索树的状态记为s，与之对应的智能运维系统多维监控指标异常根本原因集合记为S。状态s由3个变量加以描述，分别为访问计数、集合S的潜在分数以及状态s转换后的新状态s'，前2个变量的数学表示方法为N（s，a）、ps（s）。将状态s转化为状态s'的动作值记为Q（s，a），其计算过程如公式（10）所示。

Q（s，a）=max ps（S（u）），u∈{s'} （10）

式中：u为集合。

MCTS算法通过4个步骤进行根因分析。第一步为选择。目标是从其自身的搜索树中选择需要扩展的数据节点，从搜索树的根节点开始，遍历每个节点。当执行此步骤时，应使用上置信界（Upper Confidence Bound，UCB）算法实现对节点的选择，但是UCB算法会对全部节点进行一次初始化处理，此时如果以相同概率初始化全部节点，就会浪费时间和空间，因此此处采用渐进展开策略选取扩展节点。逐层计算每个元素的潜在得分ps（e），元素e根据计算结果排序，后以排定的次序再利用UCB算法得到高分元素。通过上述步骤，就能够在合理、有效的时间范围内及时寻找到具有最高潜在分数的节点。第二步为添加。这一步骤的目的是拓展MCTS，增加新状态s'。s'应满足表达式S（s'）=S（s）∩{e*}，在该表达式中，e*为集合，是从集合{e1，e2，…，en}中选择的子集，以剩余元素的潜在得分为选取e*中子元素的标准。第三步为计算。计算各元素的ps、N及Q。第四步为反馈。从MCTS的根节点到状态节点s'，形成搜索路径，更新该路径上所有节点的访问计数和动作值。

2.4 基于Apriori算法的分层剪枝方法

分层剪枝的作用是进一步降低算法的计算量，通过剪枝操作将不可能成为根因的元素集合排除在搜索范围之外。分层剪枝方法基于Apriori算法，属于数据挖掘领域的关联规则学习算法，具有先验功能。假设B中存在一层数据，将该层记为l，运用MCTS原理从中获取最大潜在分数集合，将该集合记为BSet（l，B）。由于父元素和子元素的潜在分数水平具有一定的继承性，父元素得分高说明子元素的得分也较高，因此可将集合BSet（l，B）以外的元素全部进行修剪，l+1层中将不再出现潜在分数较低的子元素，由此便简化了搜索树。

3 算法性能试验及结果分析

3.1 试验数据源介绍

以真实的智能运维系统为数据源，采集A、B、C这3种数据集，采集时长为70天，采集频率为1次/min，因此每个数据集中包括100 800条运维数据。将前55天的数据作为模型训练的样本集，后15天的数据作为模型检验的数据集。数据集可形成四阶数据立方体，每层的根因集合元素数量≤5个，因此4层数据最多包括20种异常根因。智能运维系统样本数据示例见表1。

3.2 算法性能优劣的评价指标

算法有异常定位和根因分析2种功能，性能评价的指标均为召回率（Recall）、精确率（Precision）、F-score，其对应的计算过程如公式（11）～公式（13）所示。

（11）

（12）

（13）

式中：TP为被模型预测为正类的正样本；FP为被模型预测为正类的负样本；FN为被模型预测为负类的正样本；F-score为召回率和精确率的加权调和平均值。

3.3 试验方法以及结果分析

3.3.1 算法异常定位性能试验

3.3.1.1 设置试验对照组

为了检验文章提出的算法对多维指标异常检测与定位的性能，将异常检测中的经典算法Dount（基于VAE的Web应用周期性KPI无监督异常检测）和Opprentice算法作为试验对照组。

3.3.1.2 试验结果及分析

3种算法对样本数据的异常检测结果见表2。从表2可知，本研究提出的改进算法在精确率、召回率以及F-score这3项性能指标的得分上均高于Dount算法和Opprentice算法，并且在3种数据集上表现出稳定性。

3.3.2 算法根因分析性能试验

为检验算法在根因分析中的性能，同样设置2个对照组，分别为HotSpot算法和Adtributor算法，将B作为性能检测的数据源，得到的试验结果见表3。从表3可知，本文提出的根因分析优化算法在精确率和召回率2项指标上全面优于HotSpot算法和Adtributor算法。

4 结语

针对智能运维系统多维监测指标的异常定位算法应具备异常信息检测以及根因分析的功能。变分循环网络能够整合长短期记忆网络和变分自编码器，可从时序变化层面监测系统中的异常情况。在根因分析方面，经过符号定义、潜在分数计算以及分层剪枝等操作，以MCTS算法为基础设计出优化方法，缩小了搜索空间，降低了算法的计算量。试验结果表明本研究提出的新算法具有良好的性能。

参考文献

[1]王雅鑫，赵月爱.基于KL退火的VRNN视频异常预测算法研究[J].太原师范学院学报（自然科学版），2023，22（1）：38-44.

[2]管延霞，刘逊韵，刘运韬，等.面向多智能体博弈的并行蒙特卡洛树搜索算法研究[J].计算机工程与科学，2022，44（12）：2128-2133.

[3]宋英健，侯荣旭，孙嘉荣，等.动态混合局面评估MCTS算法在爱恩斯坦棋中的应用[J].沈阳工程学院学报（自然科学版），2022，18（3）：72-76.

[4]赵晓杰，陈晔.面向计算机实验室智能运维的网络设备视觉识别算法研究[J].西安文理学院学报（自然科学版），2023，26（2）：39-43.

[5]贾静茹，包健，刘涛，等.智能运维体系在超大型数据中心中的实践[J].长江信息通信，2022，35（9）：133-136.