课堂情境下二年级学生搭配策略的变化与启示

【摘 要】搭配问题（又称笛卡尔积模型）是典型的整数乘法情境之一。基于文献修订形成学生解决搭配问题的策略水平分析框架，在学生初步学习了等组模型及倍的概念后，先分为两部分四个问题深入研究，再通过问卷和访谈调查分析学生搭配策略水平层次，最后提出相应建议：（1）可在二年级引入搭配问题的教学，丰富学生的乘法认识；（2）宜分课时教学搭配问题，先达成加法—乘法过渡水平的认识，再在此基础上进行反思、优化，确保更多学生受益；（3）倡导推理的课堂文化，勿急于将问题类型化。

【关键词】搭配问题；策略水平；分析框架；乘法模型

一、 问题提出

在《义务教育数学课程标准（2022年版）》中，数与代数是学生数学学习的重要领域。在小学阶段包括“数与运算”和“数量关系”两个主题。“数量关系”的教学，重点在于让学生感悟加法模型和乘法模型的意义。相较于加法模型，乘法模型理解起来更为复杂。Greer曾归纳出四类典型的整数乘法问题情境［1］276-295，具体包括：（1）等组模型，如每盘有4个桃子，3盘共有多少个桃子？（2）倍数模型，如小猴子有4个桃子，大猴子的桃子数量是小猴子的3倍，大猴子有多少个桃子？（3）笛卡尔积模型，在我国教材中通常称为搭配问题，如3件上衣和4条裤子可以搭配出多少套不同的套装？（4）长方形面积模型，如一个长方形长4厘米，宽3厘米，求它的面积。这四类模型分布在小学数学的不同学段中。其中，等组模型本质上是基于部分—整体关系的分析，属于加法性质的解释。而搭配问题对学生的挑战较大。有研究指出，即使第三学段的学生也未必能完全理解和解决这类问题。［2］

当前，一些教材将搭配问题移至二年级，要求学生通过有序枚举解决问题，甚至期望学生将其与乘法表征相关联。这样的教材设计是否能实现预期的效果和目标呢？在实际教学中，笔者发现了一些形式化掌握的现象。例如，学生可能只会解决采用典型句式陈述的搭配问题（如前面提到的衣服搭配裤子），但无法识别非典型的搭配问题，或者将句式相似但非搭配问题的误认为是搭配问题。此外，一些学生虽然能够列出乘法算式，却无法说明算式的意义。因此，有必要研究：二年级学生是如何理解搭配问题的？教师应如何帮助他们逐步掌握这一乘法模型？

二、相关研究

（一）搭配问题的内容分析

在当前的教学实践中，搭配问题通常与等组模型联系在一起，将乘法运算解释为相同加数相加。如在“衣服搭配裤子”情境中，3件上衣和4条裤子通过有序搭配可得到：4条裤子（搭配第1件上衣）+ 4条裤子（搭配第2件上衣）+ 4条裤子（搭配第3件上衣）= 4×3=12（套）套装。这种解释与观察到的学生解决问题的实际行为相吻合。但搭配问题的数学意义不止于此。

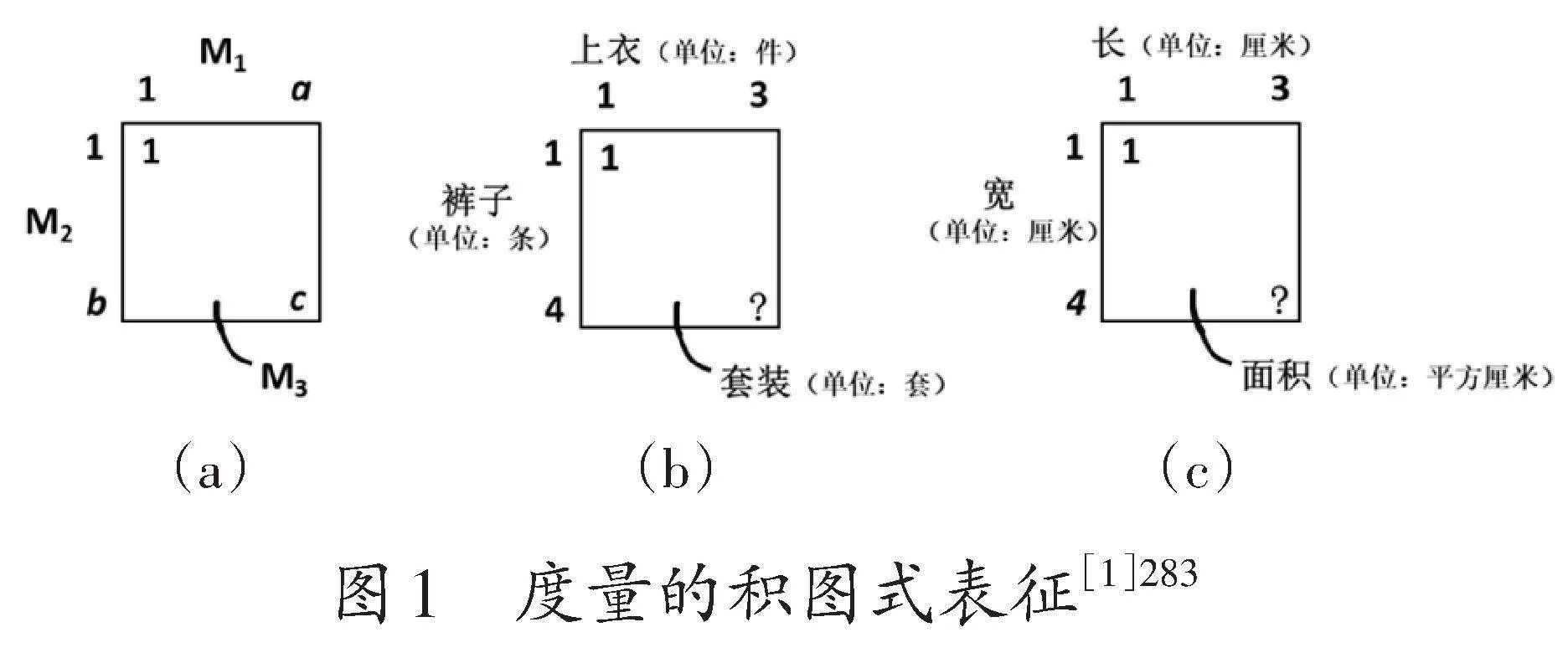
Vergnaud将乘法问题分为三类结构：度量同构、度量的积以及多重比例问题。［3］其中，度量的积涉及两个度量空间M1和M2，它们共同映射出第三个新的度量空间M3，包含搭配和长（正）方形面积两个子类，其图式表征如图1所示。以图1（b）为例：横边表示上衣数量，按“1件”为单位度量，共有3件；纵边表示裤子数量，按“1条”为单位度量，共有4条；两者复合成的平面表示新数量——套装，按“1套”为单位度量，可得出4×3套套装。

在“度量的积”这一结构中，涉及两个不同量纲的数量相乘产生一个新数量的过程。这里一个数量源自上衣集合，另一个数量来自裤子集合，并通过乘法运算，产生了一个新的集合——套装集合。因此，搭配问题可以这样理解：1件上衣和1条裤子构成1套套装。套装的数量与上衣的件数和裤子的条数分别成正比，如图2所示。这种对乘法复合及比例关系的理解，对学生后继学习乘法内容具有重要的促进作用。

（二）学生解决乘法问题的策略水平分析

学生在解决乘法问题时所采用的策略往往反映出他们对乘法模型的理解和思维发展的程度。Clark和Kamii通过“鳗鱼问题”（倍数模型）对1～5年级的学生进行访谈，将他们的乘法思维发展水平划分为五个水平层级，具体分析如表1所示。［4］ Jacob和Willis通过文献研究，也归纳出学生乘法认知发展的五个阶段：一一对应计数、加法性合成思考、一多对应计数、乘法关系以及算子运算。其中加法性合成与一多对应计数仍被视为加法思维的范畴，一多对应计数阶段更是标志着学生思维发展水平从加法思维向乘法思维过渡。一旦学生认识到乘法关系，便意味着他们已经进入了乘法思维阶段。而能够进行算子运算的学生，则被视为完全具备乘法思维。［5］

上述两个分析框架具有一致性，均表明学生在建构和理解乘法模型的过程中，从加法思维逐步过渡到乘法思维。然而，目前的研究尚未利用搭配问题来探究学生的思考过程，因此尚不清楚学生在学习搭配问题时思维上的变化。本研究旨在整合现有的评估框架，观察和分析本地学生在课堂情境中解决搭配问题时的认知变化，探究他们对搭配模型的理解可能达到的水平，以及在理解过程中遇到的难点，从而为教师精准设计教学提供参考依据。

三、研究设计

（一）研究对象

本研究选定杭州市一所普通公办小学二年级某班共36名学生作为研究对象，其中男生19名，女生17名。该班级学生使用的是浙教版教材，并且在学习搭配问题前，已经掌握了乘法的基础知识，包括乘法的初步认识（等组模型）、表内乘法以及倍的初步认识。担任教学的教师毕业于师范专业，具有8年教龄。

（二）教学过程

本研究将“搭配问题”的教学分为两个课时。第一课时重在让学生通过自主探索和同伴交流，掌握有序搭配的方法。这一方面已有许多精彩的教学案例［6］，在此不赘述。第二课时则引导学生对搭配方法进行深入反思，并尝试将他们的理解提升到乘法思维水平。具体教学分为两部分。

第一部分设置了两个相关联的问题，相当于例题，目的是在数值较大且存在倍数关系的情况下，引导学生运用更简洁高效的乘法策略。具体问题如下。

问题1：有4件上衣和5条裤子，1件上衣搭配1条裤子，一共可以搭配出几套不同的服装？

问题2：有8件上衣和5条裤子，1件上衣搭配1条裤子，一共可以搭配出几套不同的服装？

第二部分为学生独立练习环节，同样设置了两个问题，其中一个问题相对常规，另一个问题则刻意改变了常规的叙述方式，并增加了一些干扰信息。具体问题如下。

问题3：一家商店的三明治是可以自己搭配的。

可选的面包有3种：

可选的馅料有4种：

一共可以搭配出多少种不同口味的三明治？

问题4：图书馆新到3本不同的科学杂志和6本不同的故事书。1个同学可以借2本读物。如果从科学杂志和故事书里各选1本，一共有多少种不同的借法？

（三）编码研究

第二课时结束后，研究团队收集了学生提交的包含四个问题的作业纸，共32份有效问卷，然后对有效问题进行编码和访谈。

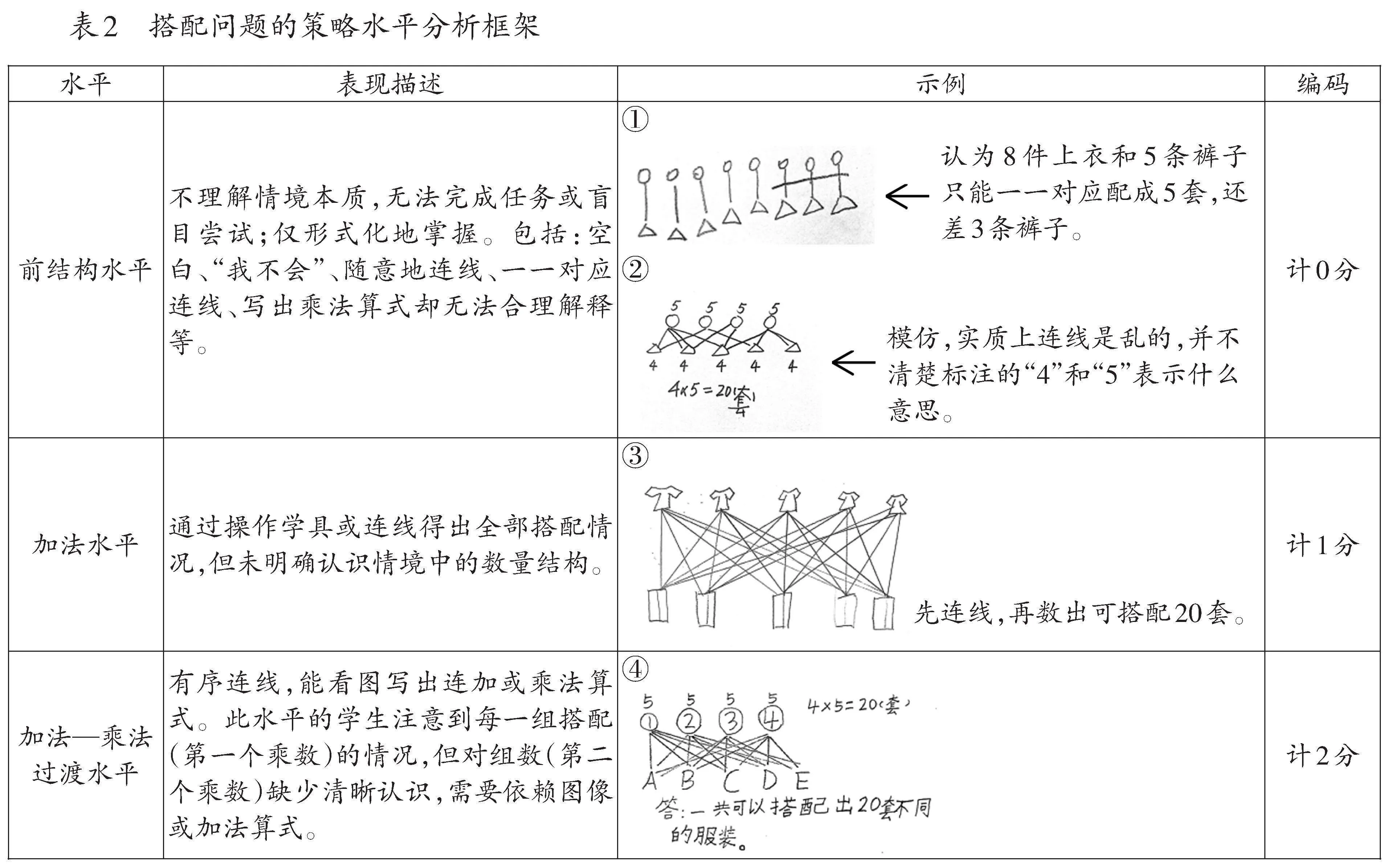
首先，团队浏览了全部学生采用的解题策略，并根据这些策略对先前的评估框架进行了整合与调整（如表2）。接着，第三作者根据学生平时的表现，挑选出好、中、弱的学生各3名。第一作者和第三作者共同对这些学生的作业进行编码，以方便分析该评估框架对学生答案的覆盖面。然后，对于那些表达不够明确尤其是仅提供乘法算式作业纸的学生，第一作者和第三作者与他们进行了面对面访谈，以确保了解学生的解题思路。最后，第一作者和第三作者分别对全部32名学生的作业进行了编码，对于采用不止一种解题策略的作业，按照最高水平的策略进行评分。计算结果显示，第一作者和第三作者两位编码者的归类一致性指数为0.875。对于编码结果不一致的作业，邀请第二作者加入讨论，共同确定了最终的编码结果。

四、研究结果

（一）整体情况

经过两个课时的学习，大多数二年级学生能够有效地解决搭配问题。超过60%的学生达到了乘法水平（主要为乘法水平1），具体数据如表3所示。

（二）不同水平策略在课堂中的变化

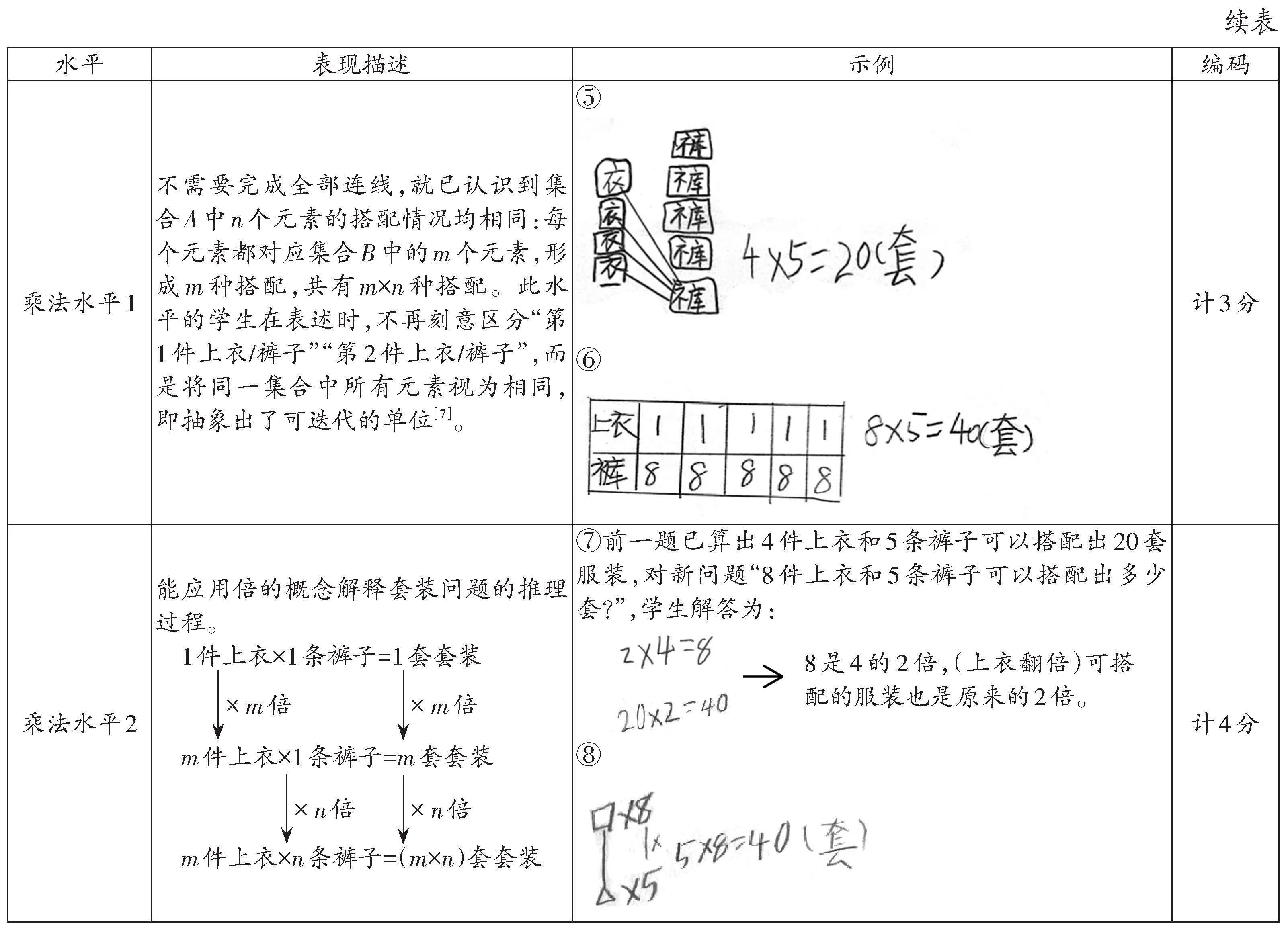
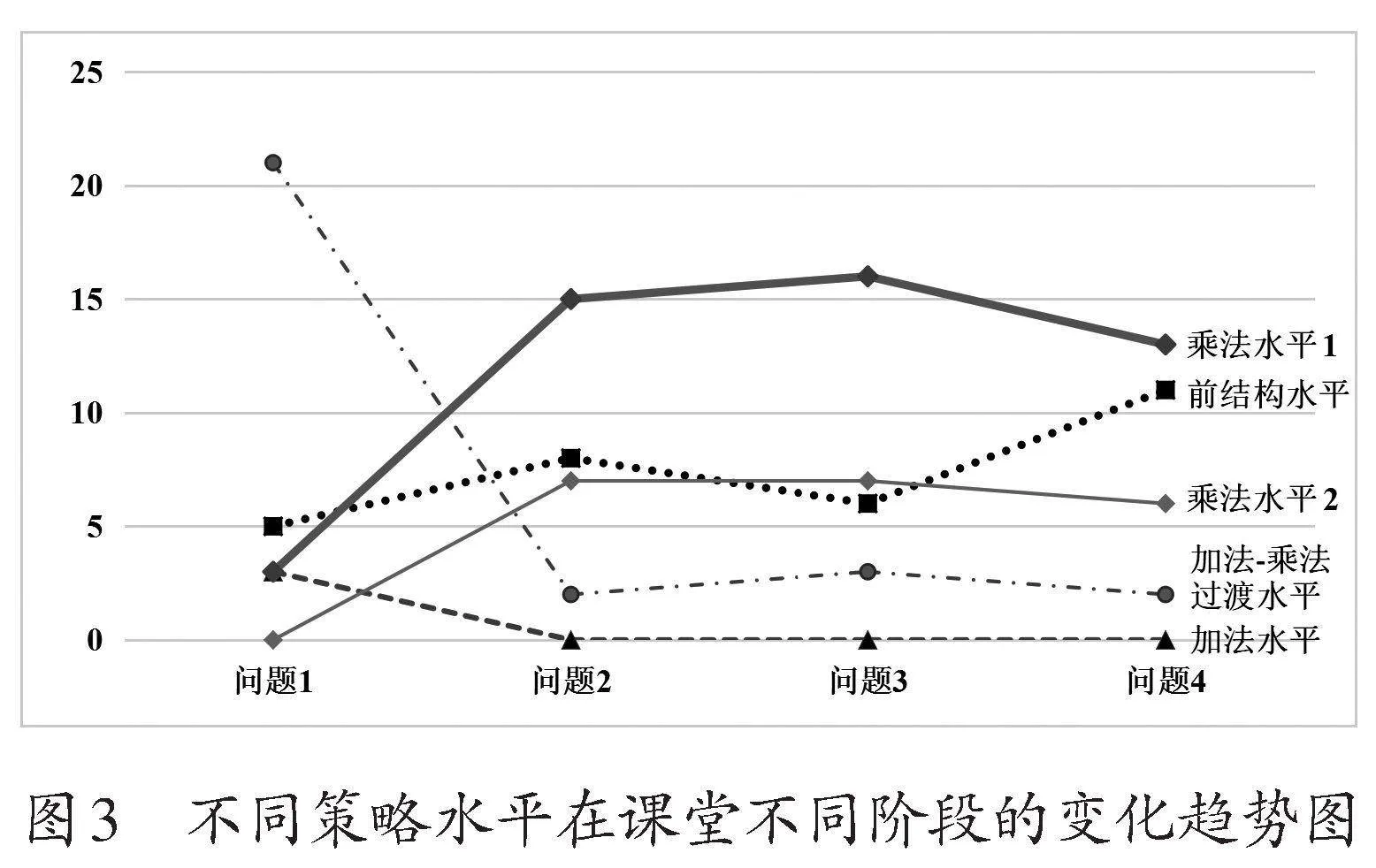
学生解决搭配问题的策略变化体现了Siegler所描述的“叠波”现象［8］，即学生同时掌握多种策略，这些策略相互竞争，整体上呈现出优化和进步的趋势。如图3所示，在第二课时中，加法水平策略仅在问题1中出现，随后很快被淘汰。加法—乘法过渡水平的策略明显减弱，逐渐被更高级的乘法水平策略所取代。乘法水平1策略逐渐成为主流，大多数学生能够将搭配问题与等组模型联系起来，将集合A（或B）中每个元素的可搭配数量看作第一个乘数，集合A（或B）中元素的个数看作第二个乘数，建立搭配问题的乘法结构。约20%的学生开始展现出乘法水平2的理解，能够超越具体计算，基于不同搭配数量之间的关系进行增倍推理，预测搭配结果。

然而，研究者也注意到，课堂上一直存在处于前结构水平的学生，具体分析将在下一小节中展开。

（三）不同学生策略水平变化分析

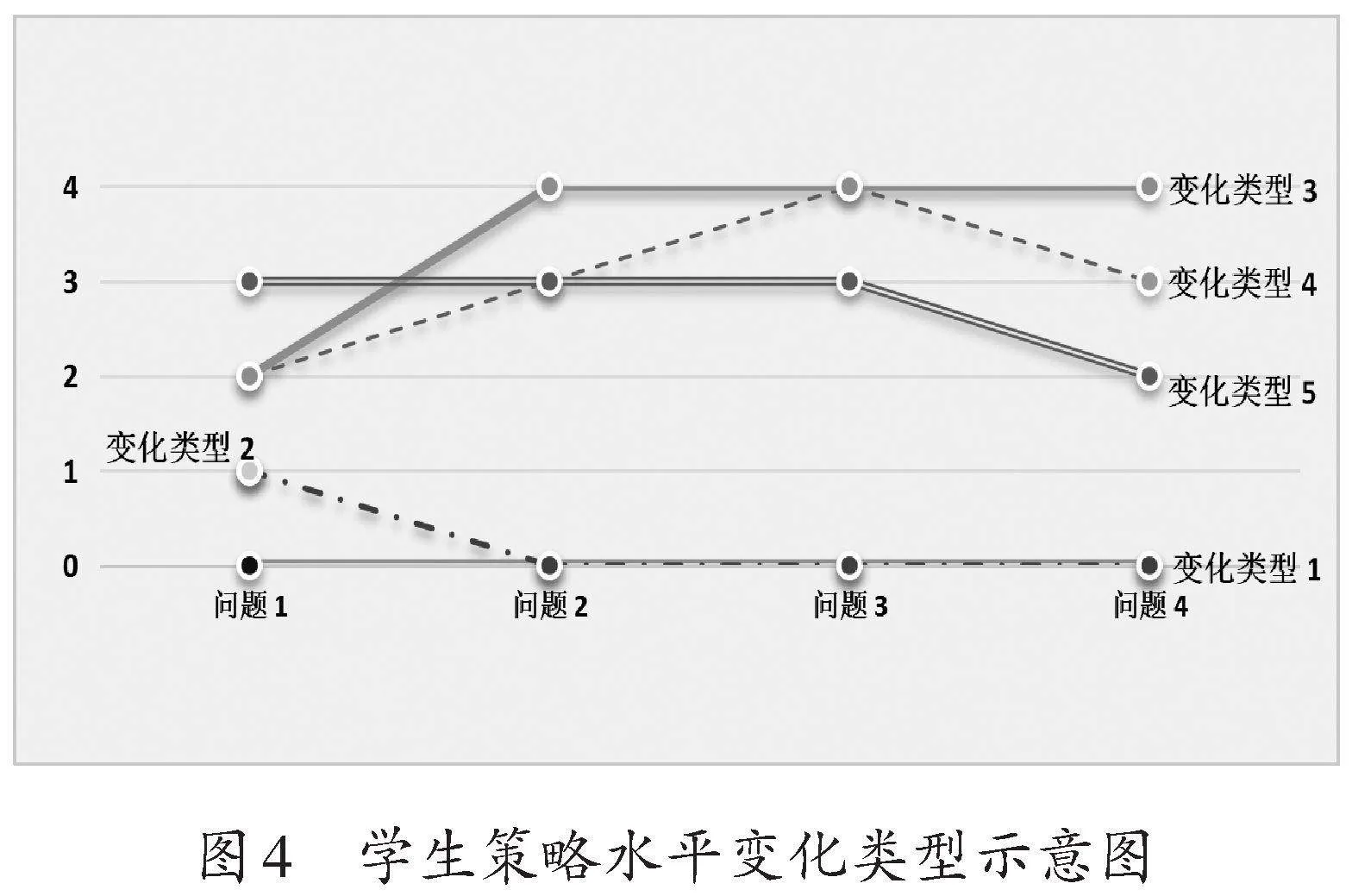
问题1的解题表现可以视为本节课学生的起点水平。一个具有启示性的现象是：在起点低于加法—乘法过渡水平的8名学生中，有7名整节课的学习都处于前结构水平，如图4变化类型1、变化类型2；而起点达到加法—乘法过渡水平的21名学生中，有17名从问题2开始即进入并保持在乘法水平，如图4中的变化类型3、变化类型4；另外3名起点为乘法水平的学生中，有2名始终保持在乘法水平，1名在遇到问题4这样的变式问题时，会重新回到加法—乘法过渡水平寻求解题方法，如变化类型5。由此，可以推断：加法—乘法过渡水平是一个关键的认知阶段。在未达到这一水平之前，学生难以理解乘法结构，即使模仿乘法计算，也无法发展乘法思维。同时，刚刚开始形成乘法思维的学生在遇到困难时，也需要回到这一水平重新反思和整理自己的经验，以便进一步提升。

此外，一些学生在解决搭配问题4时，策略水平出现退步，甚至急剧下降至前结构水平。一方面，这说明搭配问题对二年级学生确实具有一定的难度，他们需要更多的解题经验才能形成有效的概括，更好地掌握乘法模型；另一方面，这也提醒教师在进行教学和评价时，要谨防问题类型化，以免掩盖学习中的工具性理解。

五、教学启示

尽管本次研究的样本规模较小，可能无法全面反映所有二年级学生的思维状况，且研究数据是在课堂环境中收集的，无法排除学生间有相互借鉴的可能性，但研究结果依然提供了一些值得关注的学习证据。首先，大多数二年级学生具备了有效解决常规搭配问题的能力，超过60%的学生能够达到乘法水平；其次，加法—乘法过渡水平是学生发展中的一个关键时期，在此期间，“可迭代的单位”概念的形成是学生理解搭配问题数量结构、发展乘法思维的基础。基于这些研究结论，笔者提出以下教学建议。

（一） 在二年级引入搭配问题的教学

本研究表明，只要给予学生操作和反思的机会，二年级学生解决搭配问题是完全可能的，他们生成乘法水平理解的可能性也相当大。目前，大多数教材都是在二年级开始乘法教学，但通常仅将乘法与等组模型相联系，对乘法的解释仅停留在相同加数相加的水平上，这不利于学生乘法思维的发展。将搭配问题融入教学，可以丰富学生对乘法的理解，并更好地与后续学习内容衔接。

（二）分课时教学搭配问题

从理解和建构乘法模型的角度出发，建议教师分课时教学搭配问题。第一课时应侧重于操作实践，在实际操作的基础上，让学生认识一个集合中每个元素的搭配情况是相同的（如4件上衣搭配5条裤子，每件上衣都可以搭配出5套服装；3种面包搭配4种馅料，每种面包都可以搭配出4种三明治……），从而初步抽象出“可迭代的单位”概念。第二课时则注重反思，鼓励学生在不依赖具体操作的情况下，预期搭配后的数量结构，并采用乘法来解释和解决问题。至于这两课时是集中进行，还是分散安排，甚至跨学期实施，可以进一步探索。需要注意的是，那些尚未达到加法—乘法过渡水平的学生，在后续学习中会遇到困难。

（三）倡导推理意识，树立积极的数学观

在搭配问题的学习过程中，笔者发现许多二年级学生倾向于将解决问题等同于列式计算，急于列出算式，而忽略了对情境意义的深入分析（如表2中前结构水平示例）。因此，迫切需要营造一个鼓励推理的课堂文化，帮助学生树立积极的学习信念。教师可以采取以下措施：（1）给予学生充足的时间读题，并讨论题目的意思，而不是急于进入“识别问题类型—提取标准算法”的程式；（2）鼓励学生尝试不同的方法来解决问题，充分体验通过实物操作、画图、枚举等手段进行分析和说理的过程。有研究表明，当学生在解决问题时，意识到“不一定非要进行算术运算，而只要思考问题，并向他人解释自己的思考过程，就常常会从沮丧转变为兴奋和迷恋”［9］。这正是吸引学生深度参与数学学习、发展数学思维的关键所在。

参考文献：

［1］GROUWS D A.Handbook of research on mathematics teaching and learning［M］. New York：Macmillan Publishing Company，1992.

［2］HART K M.Children’s understanding of mathematics：11-16［M］.Windsor：NFER-Nelson，1981：23-47.

［3］LESH R，LANDAU M. Acquisition of mathematics concepts and processes［M］. New York：Academic Press，1983：127-174.

［4］CLARK F B，KAMII C. Identification of multiplicative thinking in children in grades 1-5［J］. Journal for research in mathematics education，1996，27（1）：41-51.

［5］JACOB L，WILLIS S.Recognising the difference between additive and multiplicative thinking in young children［C］.Sydney：24th Annual Conference of the Mathematics Education Research Group of Australasia，2001.

［6］朱志明，江益珍.巧妙渗透 凸显精彩：特级教师吴正宪“搭配中的学问”教学片段赏析［J］.教学月刊·小学版（数学），2011（9）：31-32.

［7］STEFF L P. Schemes of action and operation involving composite units［J］. Learning and individual difference，1992，4（3）：259-309.

［8］SIEGLER R S. Emerging minds：the process of change in children’s thinking［M］. New York：Oxford University Press，1996：86-87.

［9］NUNES T，BRYANT P. Using mathematics to understand the world［M］. London： Routledge，2022：116.